1. 基本思想
分支限界法(branch and bound method)是求解纯整数规划或混合整数规划问题的经典方法,在上世纪六十年代由Land Doig和Dakin等人提出。这种方法灵活且便于用计算机求解,目前已经成功运用于求解生产进度问题、旅行推销员问题、工厂选址问题、背包问题及分配问题等。算法基本思想如下:
- 以广度优先或以最小耗费(最大效益)优先的方式搜索问题的解空间树
- 分支限界法中,每一个活结点只有一次机会成为扩展结点,活结点一旦成为扩展结点,就一次性产生其所有儿子结点,其中导致不可行解或导致非最优解的儿子结点被舍弃,其余儿子结点被加入活结点表中
- 然后从活结点表中取下一结点成为当前扩展结点
- 重复上述结点扩展过程,直至到找到所需的解或活结点表为空时为止
2. 分支限界法与回溯法的区别
- 求解目标不同
- 回溯法的求解目标是找出解空间树中满足约束条件的所有解
- 分支限界法的求解目标则是尽快找出满足约束条件的一个解,或是在满足约束条件的解中找出在某种意义下的最优解
- 分支限界法通常用于解决离散值的最优化问题
- 搜索方式不同
- 回溯法以深度优先的方式(遍历结点)搜索解空间树
- 分支限界法以广度优先或最小耗费优先的方式搜索解空间树
- 对扩展结点的扩展方式不同
- 分支限界法中,每一个活结点只有一次机会成为扩展结点
- 活结点一旦成为扩展结点,就一次性产生其所有儿子结点
- 存储空间的要求不同
- 分支限界法的存储空间比回溯法大得多,因此当内存容量有限时,回溯法成功的可能性更大
3. 两种常见的分支限界法
- 队列式分支限界法
- 按照队列先进先出(FIFO)原则选取下一个结点为扩展结点
- 从活结点表中取出结点的顺序与加入结点的顺序相同,因此活结点表的性质与队列相同
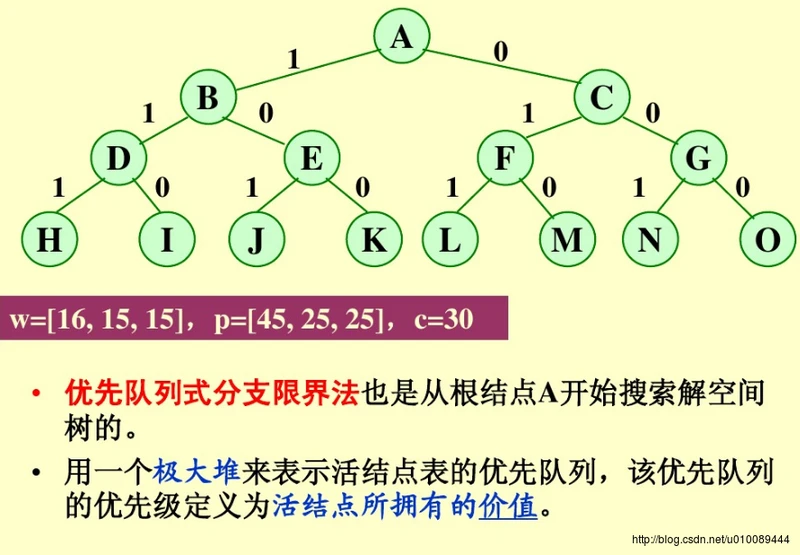
- 优先队列分支限界法(代价最小或效益最大)
- 每个结点都有一个对应的耗费或收益,以此决定结点的优先级
- 从优先队列中选取优先级最高的结点成为当前扩展结点
- 如果查找一个具有最小耗费的解:则活结点表可用小顶堆来建立,下一个扩展结点就是具有最小耗费的活结点
- 如果希望搜索一个具有最大收益的解:则可用大顶堆来构造活结点表,下一个扩展结点是具有最大收益的活结点
4. 示例: 0/1背包问题
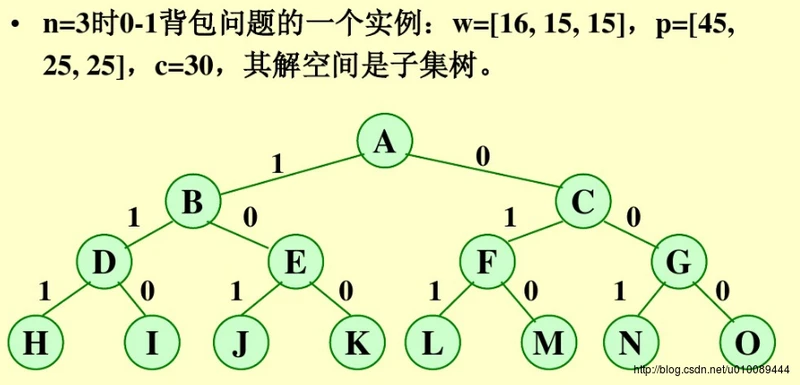
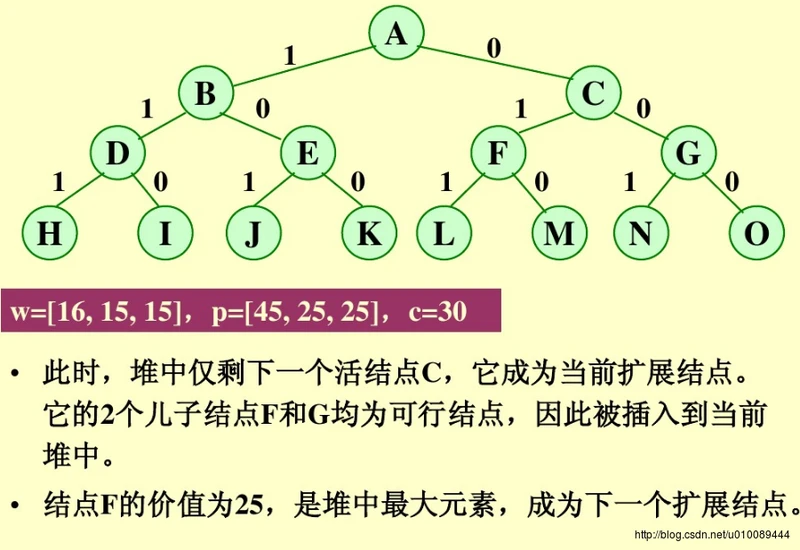
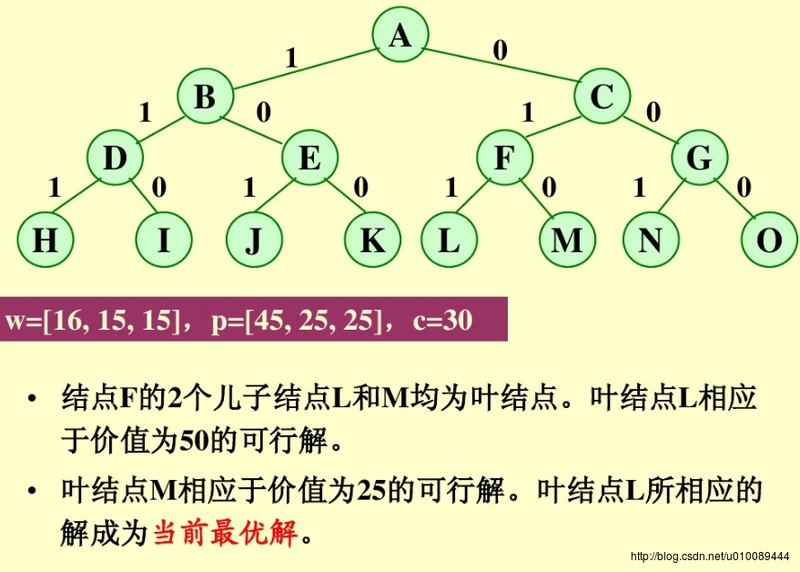
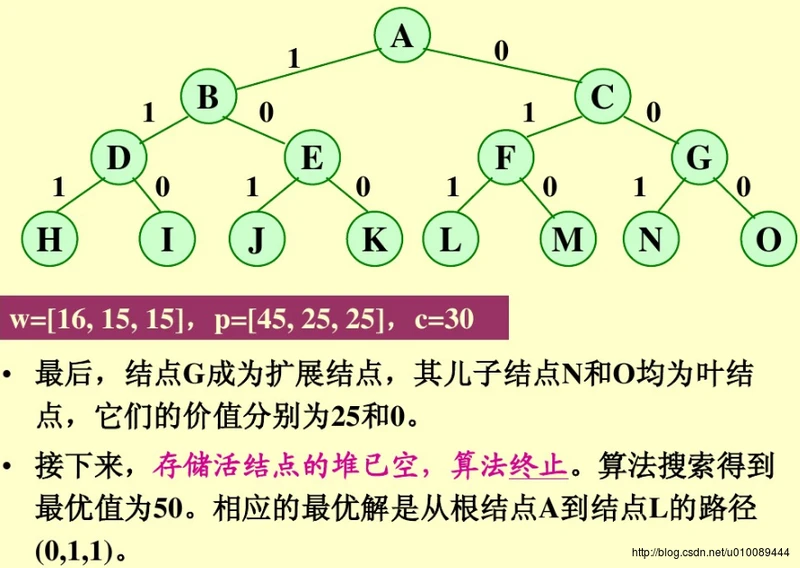
队列式分支限界法求解:
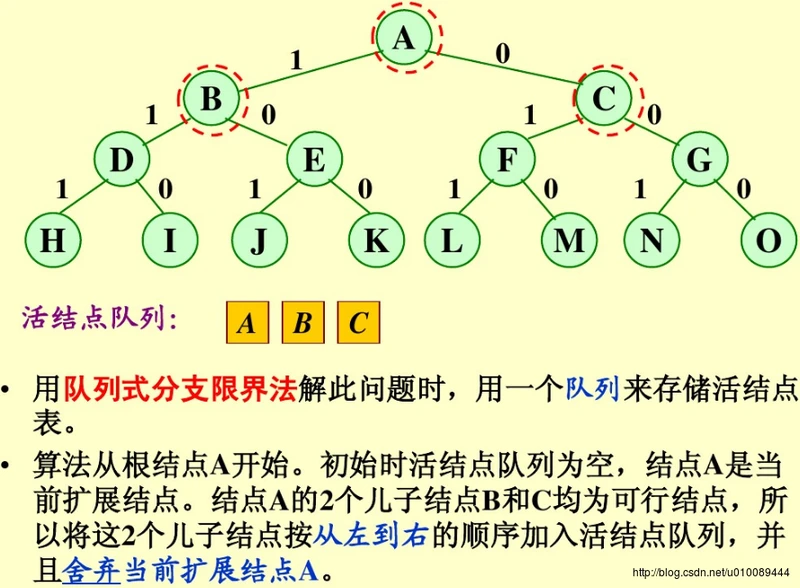

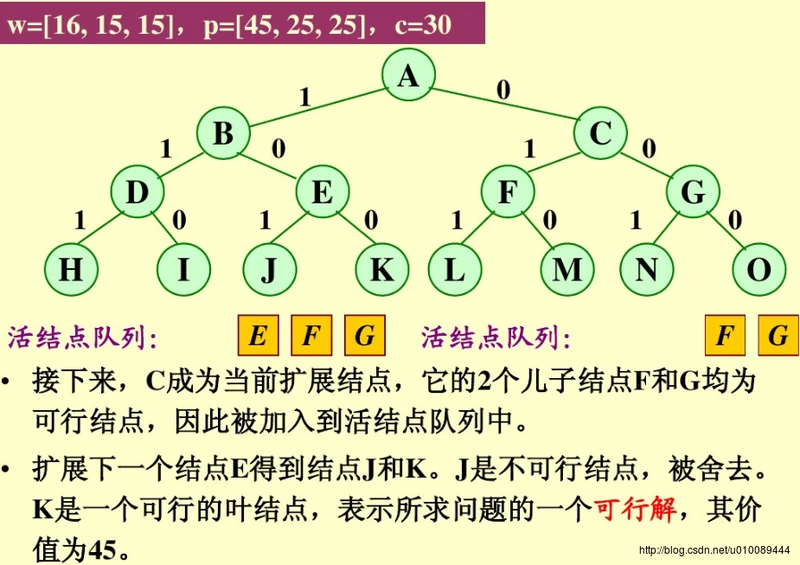
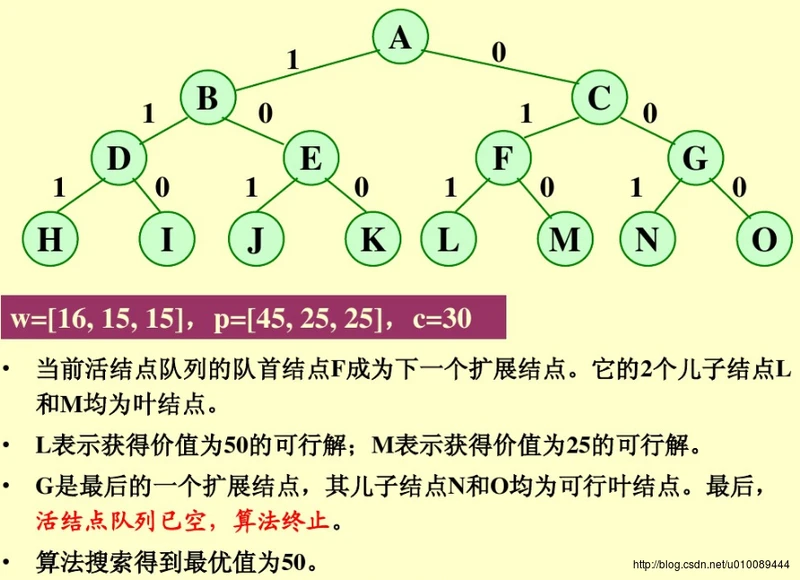
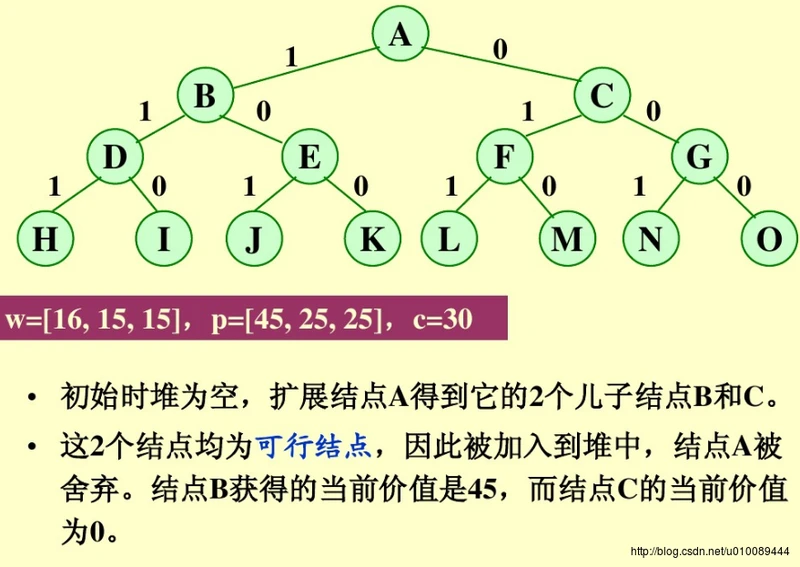
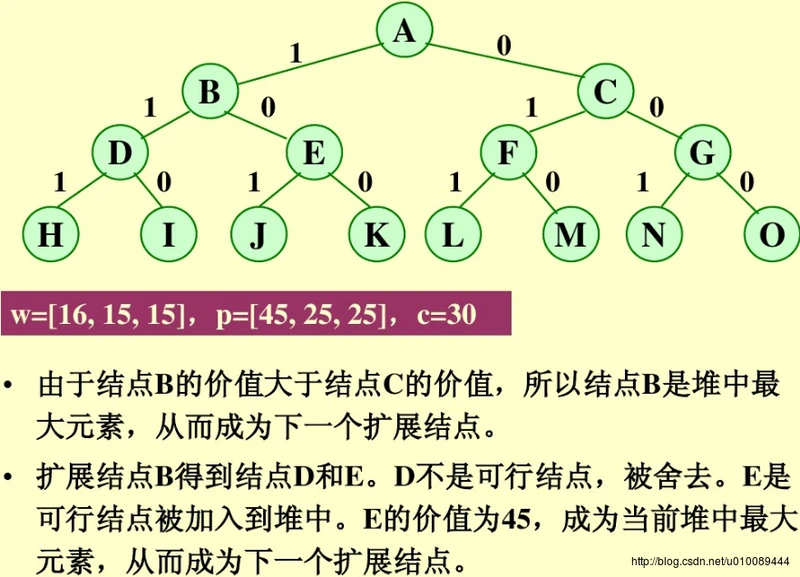
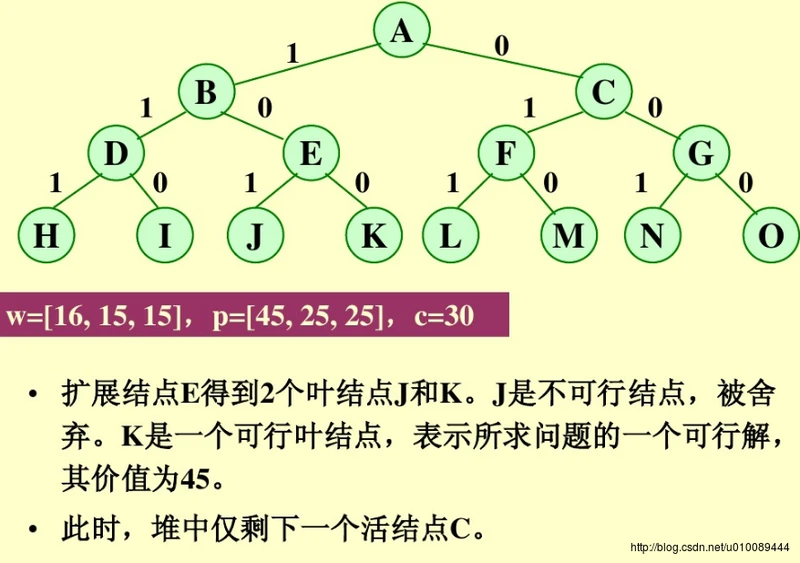
优先队列分支限界法求解: