参考资料：

《VICP: Velocity Updating Iterative Closest Point Algorithm》–Seungpyo Hong Heedong Ko Jinwook Kim
《视觉SLAM十四讲从理论到实践》–高翔

简介

追踪机器人的位姿是移动机器人领域的关键问题，ICP算法通过迭代3D空间中最近的点来求解位姿，而VICP算法在ICP算法的基础上引入了速度的更新,目的是解决运动畸变。

ICP算法

假设 X = { x i } X=\{x_i\} X={xi​}是第一帧扫描中所得到的数据点， Y = { y i } Y=\{y_i\} Y={yi​}是第二次扫描中所得到的数据点，且两帧中的数据已经进行了配对。那么优化中目标函数可以被表示为
$$\underset{R,t}{\min }J=\frac{1}{2}\sum _{i=1}^n{\Vert \left(p_i-\left(R{p}_i{}^{\prime }+t\right)\right)\Vert }_2^2$$
定义质心
$$p=\frac{1}{n}\sum _{i=1}^n\left(p_i\right),p^{\prime }=\frac{1}{n}\sum _{i=1}^n\left(p_i^{\prime }\right)$$
对函数进行一下变形，加一个$(-p+R{p}^{\prime }+p-R{p}^{\prime })$这个部分
$$\begin{array}{rl}\frac{1}{2}\sum _{i=1}^n{\Vert p_i-\left(R{p}_i^{\prime }+t\right)\Vert }^2=& \frac{1}{2}\sum _{i=1}^n{\Vert p_i-R{p}_i{}^{\prime }-t-p+R{p}^{\prime }+p-R{p}^{\prime }\Vert }^2\\ =& \frac{1}{2}\sum _{i=1}^n{\Vert \left(p_i-p-R\left(p_i^{\prime }-p^{\prime }\right)\right)+\left(p-R{p}^{\prime }-t\right)\Vert }^2\\ =& \frac{1}{2}\sum _{i=1}^n({\Vert p_i-p-R\left(p_i^{\prime }-p^{\prime }\right)\Vert }^2+{\Vert p-R{p}^{\prime }-t\Vert }^2+2{\left(p_i-p-R\left(p_i^{\prime }-p^{\prime }\right)\right)}^T\left(p-R{p}^{\prime }-t\right))\end{array}$$
这样凑得关键目的是$\left(p_i-p-R\left(p_i{}^{\prime }-p^{\prime }\right)\right)$在求和后是等于0的,如下
$$\begin{array}{rl}& \sum _{i=1}^{n}2\left(p_i-p-R{\left(p_i^{\prime }-p^{\prime })\right)}^T\left(p-R{p}^{\prime }-t\right)\right)\\ =& 2(\underset{=0}{\underbrace{\sum _{i=1}^n{p}_i-np}}-R\underset{=0}{\underbrace{\left(\sum _{i=1}^n{p}_i-np\right)}}{)}^T\left(p-R{p}^{\prime }-t\right)\\ =& 0\end{array}$$
所以，此时优化问题可以变为
$$\underset{R,t}{\min }J=\frac{1}{2}\sum _{i=1}^n{\Vert p_i-p-R\left(p_i^{\prime }-p^{\prime }\right)\Vert }^2+{\Vert p-R{p}^{\prime }-t\Vert }^2$$
观察函数可以发现，两个式子中，前一个式子含有优化变量R，后一个式子中含有R,t，所以我们可以先优化前一个式子，得到R，再令$t=p-R{p}^{\prime }$，使得后一个式子为最小值0。
即，此时优化问题变为
$$\underset{R,t}{\min }J=\frac{1}{2}\sum _{i=1}^n{\Vert p_i-p-R\left(p_i^{\prime }-p^{\prime }\right)\Vert }^2$$
为了使描述简单，定义去质心坐标，$q_i=p_i-p,q_i^{\prime }=p_i^{\prime }-p^{\prime }$，将上式子展开，有
$$\frac{1}{2}\sum _{i=1}^n{\Vert q_i-R{q}_i^{\prime }\Vert }^2=\frac{1}{2}\sum _{i=1}^n{q}_i^T{q}_i+q_i^{\prime T}{R}^{T}R{q}_i^{\prime }-2q_i^{T}R{q}_i^{\prime }$$
第一项和优化变量无关，利用旋转矩阵的正交性，$R^{T}R=I$，所以第二项也和优化变量无关，所以，优化问题可以转变为
$$\sum _{i=1}^n-q_i^{T}R{q}_i^{\prime }=\sum _{i=1}^n-\mathrm{tr}\left(R{q}_i^{\prime }{q}_i^T\right)=-\mathrm{tr}\left(R\sum _{i=1}^n{q}_i^{\prime }{q}_i^T\right)$$
这里用到的小技巧是一个行向量与一个列向量的乘积等于行向量与列向量乘积的迹。
后续证明较复杂，这里给出结论，定义
$$W=\sum _{i=1}^n{q}_i{q}_i^{\prime T}$$
现在的问题即为
$$min(-tr(RW))=maxtr(RW)$$
先给出一个定理: 假设矩阵A为正定对称矩阵，则对于任意的正交矩阵B，都有：$tr(A)\ge tr(BA)$
对W做SVD分解以后有
$$\begin{array}{rl}& W=U\Lambda V^{T}X=V{U}^T\text{ —–正交矩阵 }\\ & XW=V{U}^{T}U\Lambda V^T=V\Lambda V^T\text{ ——正定对称 }\end{array}$$
利用上面的定理：$tr(XW)\ge tr(BXW)$
tips ：这里的关键在于B是任意的正交矩阵，X也是正交矩阵，所以BX可以是任意正交矩阵。可以从刚体变换的角度理解，任意一次旋转变换都可以拆分为一个固定的旋转变换X和一个特定的旋转变换B。

所以，优化的结果为
$$R=U{V}^T$$

ICP算法伪代码

VICP

问题提出

由于激光雷达在测距的过程中采取旋转扫描的方式获取距离，所以测量到的每一个点并不是同时采集到的，如果在测量的过程中激光雷达(机器人)发生了移动的话，所测到的数据就会发生扫描失真。如下图所示，一个逆时针旋转的激光雷达在测距时发生了向前运动，那么偏左侧的数据将会测量到更短的距离，从而导致测量失真。

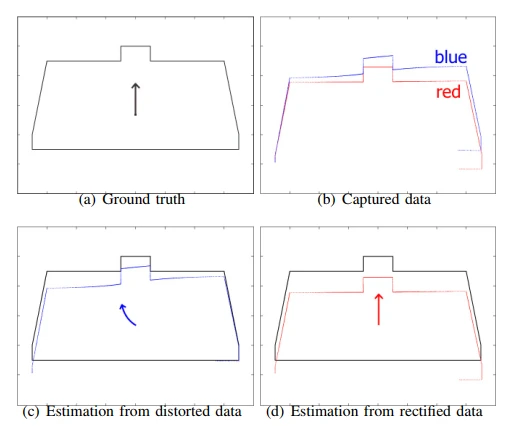
推导过程

将问题形式化，用$X^i$表示$t_i$ 时刻采集到的的数据，同样的$X^{i-1}$表示$t_{i-1}$时刻采集到的数据，两个数据之间的时间间隔为$\Delta t$，每一次扫描$X^i$都有自己的变换矩阵$T_i$。
$X^i$这次扫描的坐标系相对于$X^{i-1}$的坐标系的位姿变换矩阵可以表示为$T_{i-1}^{-1}{T}_i$，所以可以得到下面这样一个各次扫描之间刚体变换的递推式
$$x_k^{i-1}=T_{i-1}^{-1}{T}_i{x}_k^i,k=1,\cdots ,n$$
这里有点没看懂，我一直觉得是这样的$x_k^i=T_{i-1}^{-1}{T}_i{x}_k^{i-1},k=1,\cdots ,n$

两次扫描过程中速度可以用下面这个式子计算：
$$V_i=T_i^{-1}{\dot{T}}_i\approx \frac{1}{\Delta t}\log T_{i-1}^{-1}{T}_i$$
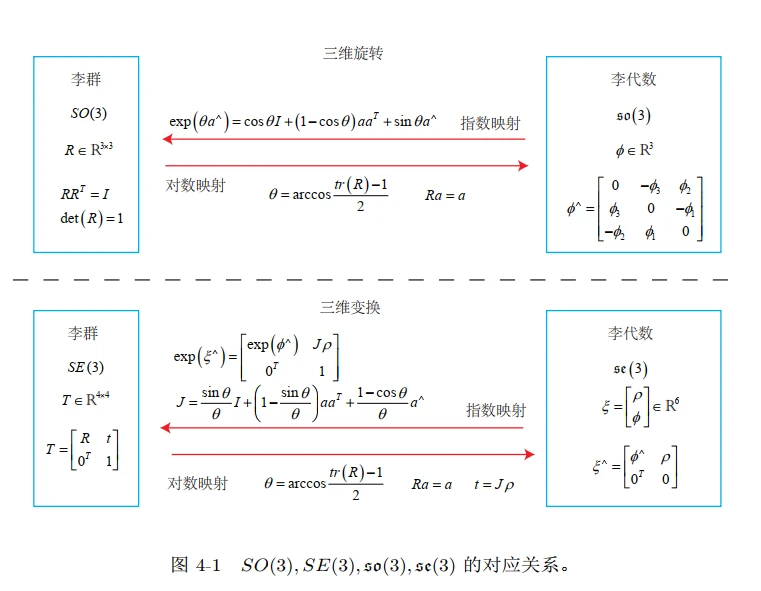
这个式子用到了李群和李代数之间的转换关系，是时候祭出14讲中的这张图了。对其次矩阵T取对数以后会得到$\left[\begin{array}{l}\rho \\ \varphi \end{array}\right]$，也就是沿三个轴的平移量和旋转量，除以时间就得到了沿三个轴的速度和角速度的近似。

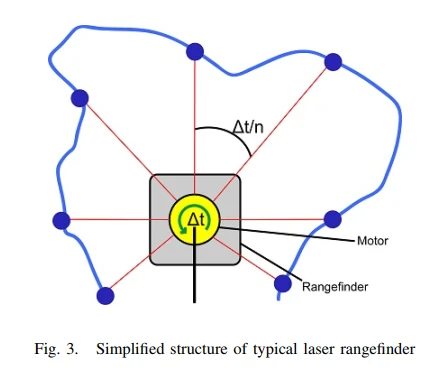
有了各帧数据之间的速度以后，我们开始处理同样一帧数据之间各个点由于激光雷达运动而产生的畸变。
下图显示了激光雷达的简化模型，假设在一帧激光雷达的数据中有n个点，每两个点之间的时间差定义为$\Delta t_s=\Delta t/n$，那么第$j$个点$(j=0,1,2...,n-1)$的位姿为
$$T(t_i+j\Delta t_s)=T_i{e}^{j\Delta t_s{V}_i}$$
这里实际上是假设在在激光雷达在打每一个点的过程中是匀速运动的，这个速度用两帧数据之间的速度，$j\Delta t_s{V}_i$就是打第$j$个点时距离第一个点激光雷达所移动的距离和角度，然后用一个指数映射将齐转换为位姿变换矩阵。之所以将齐乘在$T_i$右侧是因为这个变换是相对于连体坐标系(第一个点的位姿)的变换，运用口诀：右乘连体左乘基。

采用这种方法对数据进行修正，每个点的修正后坐标为
x ˉ ⋆ = { e j Δ V i P j ∣ j = 0 , . . . , n − 1 } \bar x^{\star}=\{e^{j\Delta Vi}P_j |j=0,...,n-1\} xˉ⋆={ejΔViPj​∣j=0,...,n−1}
就是每个点的坐标在匀速运动的假设下每个点补偿一个自己时间段内的刚体变换。

Tips

文章中的V都是广义v，实际上是由沿三个轴的速度和沿三个轴的角速度所组成的6维向量，也就是$\mathrm{se}(3)$的导数。

这里的$j$是代表第$j$个点，不是虚数单位，第一次看的时候自动脑补了欧拉公式$e^{j\theta }$，看半天没看懂。

向前修正与向后修正

上面的式子是基于向前修正，就是把后续测量到的点做一个补偿修正，另外一个方法是做一个后向修正，就是把先采集到的数据做一个预先补偿，好处是可以减少延时?(没看懂怎样减少)。

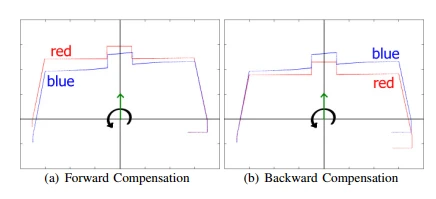
向后修正的补偿公式为
$${\bar{X}}^i=\left\{e^{(n-j)\Delta t_s\left(-V_i\right)}{x}_j\mid j=0,\dots ,n\right\}$$

VICP算法伪代码

Tips

两帧数据之间的位姿变换矩阵调用ICP算法计算，每一帧数据的补偿中用到的速度实际是调用上帧和上上帧数据计算得到的。

用for循环迭代计算位姿变换矩阵，可以减少计算量。