FreeCAD源码分析:Sketcher模块
济南友泉软件有限公司
一、功能概述
参数化建模(参数化/变量化设计)是一种基于约束的,并能用尺寸驱动模型变化的建模技术。约束与尺寸驱动是参数化建模的两个核心技术,约束是参数化建模的基础和保证,尺寸驱动是参数化建模的动力。
The variational aspect allows the user to interactively apply dimensions and constraints to a sketch. The parametric aspect ensures that the final shapes are automatically updated when a CAD element parameter is modified.
SALOME CAD With SHAPER
基于特征的建模将任何三维模型视为一系列特征的集合,而特征是一种相对简单的基本几何体或者几何操作。这样,无论模型如何复杂,都可以通过一定数量的特征按照一定方式组合而成。
Sketcher模块基于Part模块功能实现了二维草图的参数化建模功能,这类参数化建模系统主要包括几何建模引擎、几何约束求解器引擎等两大组成部分。Scketcher模块使用约束与约束求解器来创建二维几何图。
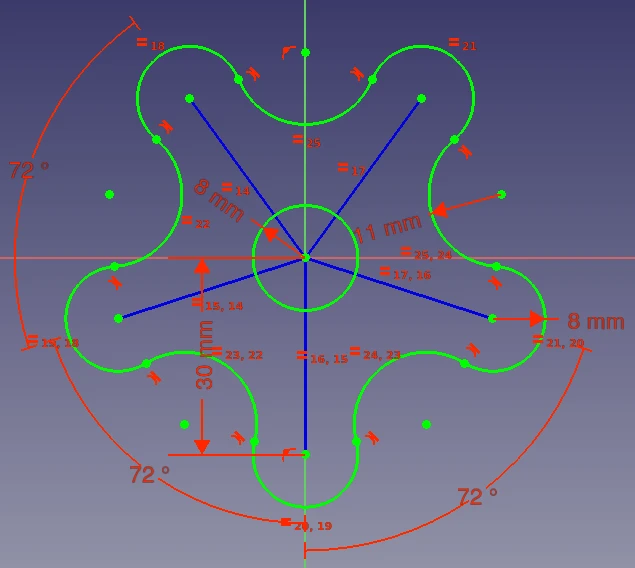
PartDesign则在Scketcher基础之上实现了基于特征的建模功能:基于Sketcher生成的二维几何体,通过拉伸、旋转等特征来增加第三维度,从而完成三维几何模型的创建。
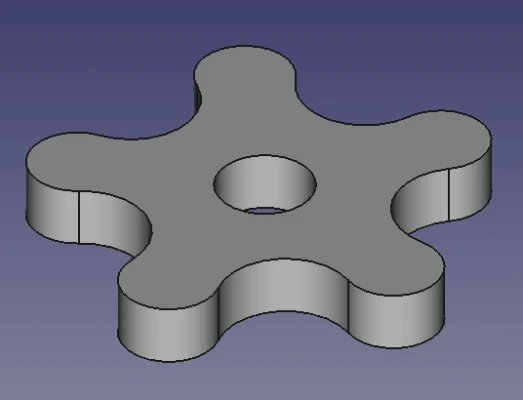
本文主要对Sketcher模块中二维草图的参数化建模进行分析。后续博文再分析PartDesign的基于特征的建模功能。
Sketcher主要功能如下:
- 二维几何元素
提供了Point、Line、Line Segment、Arc、Circle、Ellipse、Arc of Ellipse、Arc of Hyperbola、Arc of Hyperbola、Bspline等二维几何元素。
- 二维约束
提供了x坐标、y坐标、x距离、y距离、水平、竖直、点重合、点-点距离、线段长度、点-线距离、平行、垂直、相切、角度、半径、直径、相等、共线、对称等约束。
- 二维几何约束器
PlaceGCS使用约束-参数图来分解二维草图模型的几何约束关系,将其分解成独立的子问题进行求解,同时,提供了BFGS、LM(Levenberg Marquardt)、DogLeg等方法对每一个子问题的约束方程组进行优化求解,并综合各个子问题的解来获得原问题的解。
二、预备知识:CAD基础
2.1 关键技术
CAD技术从二维绘图起步,经历了线框造型、曲面造型、实体造型、特征造型等发展阶段, CAD技术正向着开放、集成、智能、标准化的方向发展。参数化、变量化等特征造型已然成为CAD常规技术,而几何约束问题求解则是参数化造型、变量化造型的核心技术。
2.2 几何元素
二维问题中,最基本的几何元素有点、直线、线段、圆、圆弧、椭圆、椭圆弧、抛物线、双曲线等。
一个几何约束系统所有的几何元素最终可以表示为二维结构点,例如线段的结构点为起始点、终止点,圆的结构点为圆心,圆弧的结构点为圆心、起始点、终止点,自由曲线的结构点为其控制点,点的结构点就是其本身,所有的约束最终可以表示成两个结构点之间的距离约束和方向约束。
每一个几何约束的位置和形状都可以由若干个独立的几何参数来确定,用于确认几何元素e的位置和形状的独立几何参数的个数称为几何元素e的自由度(Degrees of Freedoms, DOF),计作DOF(e)。
2.3 几何约束
约束可定义为受约束对象的某种限制,根据约束属性的不同,约束可分为几何约束和工程约束。
几何约束是对变量几何的类型、属性、定形和定位的限制,用于保证几何模型构造和修改的可实现性和有效性,是由用户设计意图传递给几何模型的有效手段,直接反映了几何体的形状和位置关系。几何约束包含两种类型:尺寸约束、结构约束等两类约束类型。
尺寸约束是指几何元素本身或几何元素间的显示关系,通过图上的尺寸标注表示的约束,通常包括两点之间的距离、直线与直线之间的角度、点到直线的距离等。尺寸约束是经常需要变动的,通过修改尺寸约束可进行参数驱动。
结构约束是指几何元素之间的拓扑结构关系,通常包括水平约束、竖直约束、两条直线平行和垂直、点在直线上、三点共线、两角全等、两园共心等,描述了几何元素的空间相对位置和连接方式。结构约束一般是不变动的,增加结构约束生成新的吉和实体的过程称为约束驱动。
在二维环境中,根据与约束相关的几何元素的个数,约束可分为一元约束和二元约束。
一元约束是对某个几何元素自身的约束,如水平直线、竖直直线、半径约束等。
二元约束是指两个几何元素之间约束,如点-点距离约束、线-线夹角约束等,二元约束主要用于限制两个几何元素之间的结构或位置关系,二元约束在操作视线中有主体和从提之分。例如线-线垂直,则其中第一条直线保持不变,称为主体,第一条直线保持与第一条直线垂直,称之为从体。
几何约束c引起的相关几何元素自由度的减少量,称之为几何约束的约束度(Degrees of Constraint, DOC),计作DOC(c)。大多数几何约束的约束度为1,只有少数几何约束的约束度大于1。
2.4 几何约束(满足)问题
几何约束(满足)问题(Geometric Constraint Satifaction Problem,GCSP)可表述为:给定一组几何元素和一组描述几何元素间关系的约束条件,求解满足几何约束的几何元素的布置方案。
按照几何约束问题解的个数,可将几何约束问题可以分成三类:
- 完整约束几何约束问题:几何约束问题所对应的几何图形的形状有有限个
- 欠约束几何约束问题:几何约束问题所对应的几何图形的形状有无限个
- 过约束几何约束问题:几何约束问题无解
由于在参数化设计过程中,约束模型的生成和求解是一个从不完备到完备的过程,是逐步求精的过程,也就是说大部分设计过程都是在欠约束中度过的,深入研究欠约束问题的求解具有非常重要的理论和实用价值。欠约束几何约束问题的处理能力已经成为衡量一个约束求解算法的主要指标。
[Refs. from William Bouma. 1995]----------------------------------------------------------------------
求解几何约束问题会涉及到两个核心问题:
- 判定问题是否存在解?如果存在解,如何进行求解?
- 有限解集中,哪一个是用户真正期望的解?
从软件实现来看,几何约束求解程序主要由三部分组成:用户界面、几何约束问题描述、几何约束求解等。
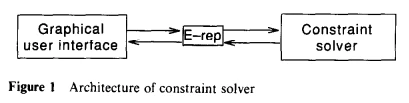
----------------------------------------------------------------------[Refs. from William Bouma. 1995]-
按照求解方式,几何约束求解算法可分为基于数值计算的几何约束求解方法、基于符号计算的几何约束求解算法、基于规则的几何约束求解方法、基于图论的几何约束求解方法等四类方法。
以下论述摘自Ait-Aoudia S等2009年发表的文章<2D Geometric Constraint Solving : an Overview>
[Refs.Ait-Aoudia S, 2009]----------------------------------------------------------------------
基于数值计算的几何约束求解方法(Numerical methods):
In a numerical constraint solver, the geometric constraints are first translated into a system of algebraic equations (linear or not). This system is then solved by applying a numerical method.Many systems have used the Newton-Raphson’s iteration to solve the set of geometric constraints.
If Newton-Raphson’s method often works well, sometimes it does not converge or it converges to an unwanted solution. An alternative method to Newton-Raphson for geometric constraint solving is homotopy or continuation.
Numerical methods are O(n3 ) or worse. These methods suffer from the lack of "geometric explanation" during the resolution process. Also, most numerical methods have difficulties for handling over-constrained or under-constrained schemes. The advantage of these methods is that they have the potential to solve large nonlinear system that may not be solvable using any of the other methods. Almost all existing solvers switch to algebraic methods when the given configuration is not solvable by the native method. Algebraic methods handle easily the 3D case. Speeding up the resolution must be considered further.
基于符号计算的几何约束求解算法(Symbolic methods):
As in the numerical solvers, the constraints are again formulated as a system of algebraic equations. However, instead of applying numerical techniques to determine a solution, general symbolic computations are undertaken to find the solution to the system of equations.
Symbolic methods are typically exponential in time and space. They can be used only for small systems.
基于规则的几何约束求解方法(Rule constructive approach):
Rule-based solvers rely on the predicates formulation. The constraints are expressed as facts and an inference engine is used to derive the solution by exhaustively applying rules.Rule-constructive approach provide a qualitative study of geometric constraints. Although it is a good approach for prototyping and experimentation, the extensive computations involved in the exhaustive searching and matching make it inappropriate for real world applications.
Rule-based solvers rely on the predicates formulation. Although they provide a qualitative study of geometric constraints, the "huge" amount of computations needed (exhaustive searching and matching) make them inappropriate for real world applications.
基于图论的几何约束求解方法(Graph constructive approach):
Graph-based algorithms for solving geometric constraint problems have two phases : an analysis phase and a construction phase. These algorithms are also called decomposition recombination methods. During the first phase the graph of constraints is analyzed and decomposed in small sub-problems. Sequences of construction steps are derived. During the second phase the recombination is carried out and the construction steps are processed to place the geometric elements.
Graph-based methods can be very efficient. In Computer-Aided Design, the graph-based approach has become dominant. However, these methods are only applicable to particular kinds of problems, typically ruler and compass constructive problems. The graph-based approach to handle efficiently the 3D case deserves further studies. The theoretical framework is no longer applicable.
----------------------------------------------------------------------[Refs.Ait-Aoudia S, 2009]
三、基于图论的几何约束求解算法
已经有不少论文对图论类几何约束求解算法做了深入总结和研究,故这里不再赘述,仅列举几篇论文资料。
- J. Owen. Algebraic solution for geometry from dimensional constraints. Proc. Symp., Solid modeling foundations and CAD/CAM applications1991. PP 397-407.
- C.M. Hoffman and R. Joan-Arinyo. A Brief on Constraint Solving, Computer-Aided Design and Applications, 2(5):655-663, 2005..
- Ait-Aoudia S , Bahriz M , Salhi L . 2D Geometric Constraint Solving: An Overview[M]. IEEE, 2009.
- C.M. Hoffman. Summary of basic 2D constraint solving, Int. Journal Product Lifecycle Management, Vol. 1, No. 2, 2006.
- W. Bouma, I. Fudos, C.M. Hoffman, J. Cai, R. Paige. A geometric constraint solver. Computer Aided Design, Vol. 27, No.6, June 1995, 487-501.
- Fudos, C.M. Hoffman. A Graph-Constructive approach to Solving Systems of Geometric Constraints. ACM Trans. on Graphics, Vol.16, N°2, April 1997, 179-216.
- A. Lomonosov ,M. Sitharam and C.M. Hoffman. Finding Solvable Subsets of Constraint Graphs. Springer LNCS 1330, G. Smolka, ed., 1997, 463-477.
- A. Lomonosov ,M. Sitharam and C.M. Hoffman. Geometric Constraint Decomposition. Geometric Constr Solving and Appl., B. Bruderlin and D. Roller, eds, 1998, Springer, 170-195.
- A. Lomonosov ,M. Sitharam and C.M. Hoffman Decomposition Plans for Geometric Constraint Problems, Part II: New Algorithms. Journal of Symbolic Computations 31, 2001, 409-428.
四、算法原理概述
基于图论的几何约束求解算法的基本思想是:1) 将几何约束问题按照约束对象之间约束关系转换成约束图;2) 分析约束图并将其拆分成可以独立求解的子问题; 3) 合并子域求解结果,得到原几何约束问题的解。
4.1 区域分解
在FreeCAD Sketcher::Sketch中,实现基于Parameter-Constraint的几何约束图构造域分解的方法,具体来说,包括以下步骤:
a) 以独立参数、约束等作为node,以约束与独立参数的关系作为依赖关系构造edge,从而生成几何约束图。
b)借助图论连通分量的概念,生成约束子图。也就是定义了子域上的几何约束问题。
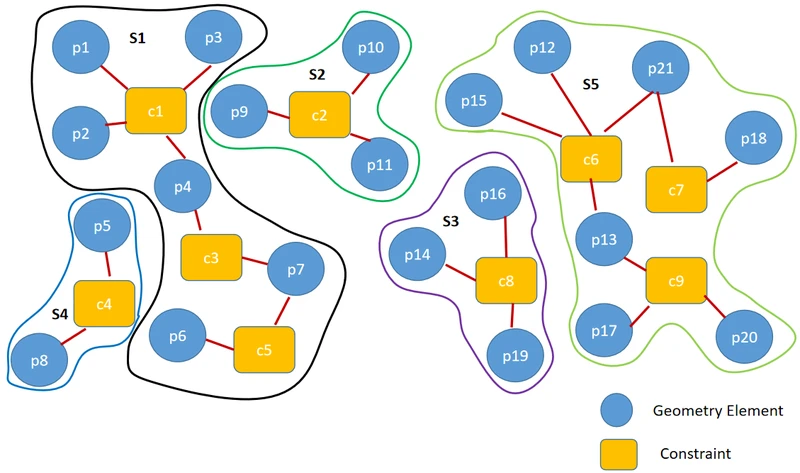
4.2 子域求解
设![\textbf{x}=\left [ x_{1},x_{2},\cdots ,x_{n}\right ]^{T}](https://yyzqsoft.com/uploads/202407/04/c636ae5969ddb21a.webp) 为待求可变参数向量,
为待求可变参数向量,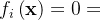 为约束方程,则几何约束问题可以表述为,
为约束方程,则几何约束问题可以表述为,
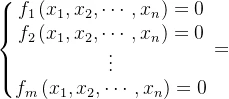
构造如下的目标函数,
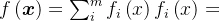
则在一定程度上,寻找草图最优解的问题可以转换为求上述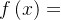 的(局部)最小值问题,即关于
的(局部)最小值问题,即关于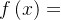 的无约束最优化问题。
的无约束最优化问题。
即,
实际上,上述即是FreeCAD Sketcher模块中几何约束图分解之后,实施子域求解的数学原理。
目前,FreeCAD Sketcher PlanGCS提供了BFGS、Levenberg-Marquardt、DogLeg等三种数值求解子域优化问题的算法。
五、数值优化算法:BFGS算法
Newton算法在计算时需要用到Hessian矩阵H, 计算Hessian矩阵非常费时, 所以研究者提出了很多使用方法来近似Hessian矩阵, 这些方法都称作准牛顿算法, BFGS就是其中的一种, 以其发明者Broyden, Fletcher, Goldfarb和Shanno命名。BFGS算法算然具有全局收敛性和超线性收敛速度,但却容易陷入局部最优而不能够有限地处理临界点。
限于篇幅,本文仅给出BFGS算法的大体思路与操作流程。对于BFGS算法感兴趣的读者可以参考袁亚湘院士编写的<最优化理论与方法>中的相关内容。
5.1 数学原理
对于无约束优化问题 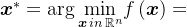
假定最优解即为极值,根据极值必要条件,上述问题提法等价于寻找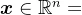 使得
使得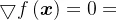
使用泰勒公式将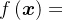 在
在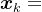 展开,忽略掉二阶以上高阶项,有
展开,忽略掉二阶以上高阶项,有
两边对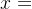 求导,得
求导,得
设时,
取最小值,则根据极值必要条件,有
,即
其中,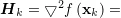 为Hessian矩阵,
为Hessian矩阵,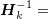 为
为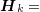 的逆矩阵,
的逆矩阵,
在BFGS算法中,是通过迭代来逼近,即
其中,
5.2 算法流程
步骤一:给定初始值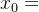 、误差阈值
、误差阈值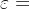 ,并令
,并令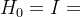 ,
,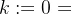
步骤二:计算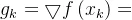 ,若
,若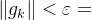 ,则算法停止,取
,则算法停止,取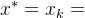
步骤三:确定搜索方向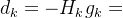 ,
,
步骤四:求步长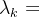 ,满足
,满足,令
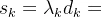 ,
,
步骤五:计算,若
,则算法结束,
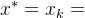
步骤六:计算
步骤七:计算
步骤八:令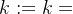 ,转至步骤三。
,转至步骤三。
六、数值优化算法:Levenberg-Marquardt算法
七、数值优化算法:DogLeg算法
八、Sketcher模块组件
Sketcher模块在Part模块已有二维几何建模功能基础之上,实现了基于约束的二维草图绘制功能。首先,根据草图中参数与约束的依赖关系,构建了“参数-约束”图,然后借助于Boost Graph Library无向图计算出多个连通分量,每个连通分量对应一个子问题,然后在子问题上使用BFGS等优化算法进行求解,最后再将求解结果合并。
8.1 Sketcher::Constraint
Sketcher::Constraint用于记录约束信息,但真正的约束对象则是在求解约束问题时由GCS::System创建。
8.2 Sketcher::Sketch
Sketcher::Sketch封装了二维几何约束问题的描述,其内部实际上是借助于GCS::System完成二维几何约束问题的求解。
8.3 Sketcher::SketchObject
Sketcher::SketchObject将Sketcher::Sketch嵌入到了FreeCAD文档对象-视图模型中,同时使用Sketcher::SketchAnalysis计算自由度。
8.4 GCS::DependentParameters
GCS::DependentParameters及其子类表示点、直线线、线段、圆弧、圆、曲线等二维几何元素。
8.5 GCS::Constraint
GCS::Constraint及其子类表示固定坐标、固定距离、水平、竖直、垂直、平行、相切等二维几何约束。
8.6 GCS::System
GCS::System利用boost graph library中无向图构建了“参数-约束”图,将二维草图模型的几何约束关系分解成独立的子问题进行求解,同时,提供了BFGS、LM(Levenberg Marquardt)、DogLeg等方法对每一个子问题的约束方程组进行优化求解,并综合各个子问题的解来获得原问题的解。
九、Sketcher工作流程
本节通过约束添加、约束求解等来分析Sketcher工作原理。
Sketcher模块提供了SketchObjectPy::addConstraint()作为统一的接口函数来添加各种各样的约束,
PyObject* SketchObjectPy::addConstraint(PyObject *args)
{
PyObject *pcObj;
if (!PyArg_ParseTuple(args, "O", &pcObj))
return 0;
if (PyObject_TypeCheck(pcObj, &(Sketcher::ConstraintPy::Type))) {
Sketcher::Constraint *constr = static_cast<Sketcher::ConstraintPy*>(pcObj)->getConstraintPtr();
if (!this->getSketchObjectPtr()->evaluateConstraint(constr)) {
PyErr_SetString(PyExc_IndexError, "Constraint has invalid indexes");
return 0;
}
int ret = this->getSketchObjectPtr()->addConstraint(constr);
// this solve is necessary because:
// 1. The addition of constraint is part of a command addition
// 2. This solve happens before the command is committed
// 3. A constraint, may effect a geometry change (think of coincident,
// a line's point moves to meet the other line's point
// 4. The transaction is committed before any other solve, for example
// the one of execute() triggered by a recompute (UpdateActive) is generated.
// 5. Upon "undo", the constraint is removed (it was before the command was committed)
// however, the geometry changed after the command was committed, so the point that
// moved do not go back to the position where it was.
//
// N.B.: However, the solve itself may be inhibited in cases where groups of geometry/constraints
// are added together, because in that case undoing will also make the geometry disappear.
this->getSketchObjectPtr()->solve();
// if the geometry moved during the solve, then the initial solution is invalid
// at this point, so a point movement may not work in cases where redundant constraints exist.
// this forces recalculation of the initial solution (not a full solve)
if(this->getSketchObjectPtr()->noRecomputes) {
this->getSketchObjectPtr()->setUpSketch();
this->getSketchObjectPtr()->Constraints.touch(); // update solver information
}
return Py::new_reference_to(Py::Long(ret));
}
else if (PyObject_TypeCheck(pcObj, &(PyList_Type)) ||
PyObject_TypeCheck(pcObj, &(PyTuple_Type))) {
std::vector<Constraint*> values;
Py::Sequence list(pcObj);
for (Py::Sequence::iterator it = list.begin(); it != list.end(); ++it) {
if (PyObject_TypeCheck((*it).ptr(), &(ConstraintPy::Type))) {
Constraint *con = static_cast<ConstraintPy*>((*it).ptr())->getConstraintPtr();
values.push_back(con);
}
}
for (std::vector<Constraint*>::iterator it = values.begin(); it != values.end(); ++it) {
if (!this->getSketchObjectPtr()->evaluateConstraint(*it)) {
PyErr_SetString(PyExc_IndexError, "Constraint has invalid indexes");
return 0;
}
}
int ret = getSketchObjectPtr()->addConstraints(values) + 1;
std::size_t numCon = values.size();
Py::Tuple tuple(numCon);
for (std::size_t i=0; i<numCon; ++i) {
int conId = ret - int(numCon - i);
tuple.setItem(i, Py::Long(conId));
}
return Py::new_reference_to(tuple);
}
std::string error = std::string("type must be 'Constraint' or list of 'Constraint', not ");
error += pcObj->ob_type->tp_name;
throw Py::TypeError(error);
}当调用SketchObjectPy::addConstraint()来添加约束,在这个函数中会触发SketchObject::solve函数,实际上这里的SketchObject就是表示新建的草图,
int SketchObject::solve(bool updateGeoAfterSolving/*=true*/)
{
// Reset the initial movement in case of a dragging operation was ongoing on the solver.
solvedSketch.resetInitMove();
// if updateGeoAfterSolving=false, the solver information is updated, but the Sketch is nothing
// updated. It is useful to avoid triggering an OnChange when the goeometry did not change but
// the solver needs to be updated.
// We should have an updated Sketcher (sketchobject) geometry or this solve() should not have happened
// therefore we update our sketch solver geometry with the SketchObject one.
//
// set up a sketch (including dofs counting and diagnosing of conflicts)
lastDoF = solvedSketch.setUpSketch(getCompleteGeometry(), Constraints.getValues(),
getExternalGeometryCount());
// At this point we have the solver information about conflicting/redundant/over-constrained, but the sketch is NOT solved.
// Some examples:
// Redundant: a vertical line, a horizontal line and an angle constraint of 90 degrees between the two lines
// Conflicting: a 80 degrees angle between a vertical line and another line, then adding a horizontal constraint to that other line
// OverConstrained: a conflicting constraint when all other DoF are already constraint (it has more constrains than parameters and the extra constraints are not redundant)
solverNeedsUpdate=false;
lastHasConflict = solvedSketch.hasConflicts();
lastHasRedundancies = solvedSketch.hasRedundancies();
lastConflicting=solvedSketch.getConflicting();
lastRedundant=solvedSketch.getRedundant();
lastSolveTime=0.0;
lastSolverStatus=GCS::Failed; // Failure is default for notifying the user unless otherwise proven
int err=0;
// redundancy is a lower priority problem than conflict/over-constraint/solver error
// we set it here because we are indeed going to solve, as we can. However, we still want to
// provide the right error code.
if (lastHasRedundancies) { // redundant constraints
err = -2;
}
if (lastDoF < 0) { // over-constrained sketch
err = -4;
}
else if (lastHasConflict) { // conflicting constraints
// The situation is exactly the same as in the over-constrained situation.
err = -3;
}
else {
lastSolverStatus=solvedSketch.solve();
if (lastSolverStatus != 0){ // solving
err = -1;
}
}
lastSolveTime=solvedSketch.SolveTime;
if (err == 0 && updateGeoAfterSolving) {
// set the newly solved geometry
std::vector<Part::Geometry *> geomlist = solvedSketch.extractGeometry();
Geometry.setValues(geomlist);
for (std::vector<Part::Geometry *>::iterator it = geomlist.begin(); it != geomlist.end(); ++it)
if (*it) delete *it;
}
else if(err <0) {
// if solver failed, invalid constraints were likely added before solving
// (see solve in addConstraint), so solver information is definitely invalid.
this->Constraints.touch();
}
return err;
}可以看到, SketchObject::solve()函数通过Sketch::setUpSketch()将草图中的几何元素、约束等设置Sketch对象,进而调用了Sketch::solve()
int Sketch::solve(void)
{
Base::TimeInfo start_time;
if (!isInitMove) { // make sure we are in single subsystem mode
GCSsys.clearByTag(-1);
isFine = true;
}
int ret = -1;
bool valid_solution;
std::string solvername;
int defaultsoltype = -1;
if(isInitMove){
solvername = "DogLeg"; // DogLeg is used for dragging (same as before)
ret = GCSsys.solve(isFine, GCS::DogLeg);
}
else{
switch (defaultSolver) {
case 0:
solvername = "BFGS";
ret = GCSsys.solve(isFine, GCS::BFGS);
defaultsoltype=2;
break;
case 1: // solving with the LevenbergMarquardt solver
solvername = "LevenbergMarquardt";
ret = GCSsys.solve(isFine, GCS::LevenbergMarquardt);
defaultsoltype=1;
break;
case 2: // solving with the BFGS solver
solvername = "DogLeg";
ret = GCSsys.solve(isFine, GCS::DogLeg);
defaultsoltype=0;
break;
}
}
// if successfully solved try to write the parameters back
if (ret == GCS::Success) {
GCSsys.applySolution();
valid_solution = updateGeometry();
if (!valid_solution) {
GCSsys.undoSolution();
updateGeometry();
Base::Console().Warning("Invalid solution from %s solver.\n", solvername.c_str());
}
else {
updateNonDrivingConstraints();
}
}
else {
valid_solution = false;
if(debugMode==GCS::Minimal || debugMode==GCS::IterationLevel){
Base::Console().Log("Sketcher::Solve()-%s- Failed!! Falling back...\n",solvername.c_str());
}
}
if(!valid_solution && !isInitMove) { // Fall back to other solvers
for (int soltype=0; soltype < 4; soltype++) {
if(soltype==defaultsoltype){
continue; // skip default solver
}
switch (soltype) {
case 0:
solvername = "DogLeg";
ret = GCSsys.solve(isFine, GCS::DogLeg);
break;
case 1: // solving with the LevenbergMarquardt solver
solvername = "LevenbergMarquardt";
ret = GCSsys.solve(isFine, GCS::LevenbergMarquardt);
break;
case 2: // solving with the BFGS solver
solvername = "BFGS";
ret = GCSsys.solve(isFine, GCS::BFGS);
break;
case 3: // last resort: augment the system with a second subsystem and use the SQP solver
solvername = "SQP(augmented system)";
InitParameters.resize(Parameters.size());
int i=0;
for (std::vector<double*>::iterator it = Parameters.begin(); it != Parameters.end(); ++it, i++) {
InitParameters[i] = **it;
GCSsys.addConstraintEqual(*it, &InitParameters[i], -1);
}
GCSsys.initSolution();
ret = GCSsys.solve(isFine);
break;
}
// if successfully solved try to write the parameters back
if (ret == GCS::Success) {
GCSsys.applySolution();
valid_solution = updateGeometry();
if (!valid_solution) {
GCSsys.undoSolution();
updateGeometry();
Base::Console().Warning("Invalid solution from %s solver.\n", solvername.c_str());
ret = GCS::SuccessfulSolutionInvalid;
}else
{
updateNonDrivingConstraints();
}
} else {
valid_solution = false;
if(debugMode==GCS::Minimal || debugMode==GCS::IterationLevel){
Base::Console().Log("Sketcher::Solve()-%s- Failed!! Falling back...\n",solvername.c_str());
}
}
if (soltype == 3) // cleanup temporary constraints of the augmented system
GCSsys.clearByTag(-1);
if (valid_solution) {
if (soltype == 1)
Base::Console().Log("Important: the LevenbergMarquardt solver succeeded where the DogLeg solver had failed.\n");
else if (soltype == 2)
Base::Console().Log("Important: the BFGS solver succeeded where the DogLeg and LevenbergMarquardt solvers have failed.\n");
else if (soltype == 3)
Base::Console().Log("Important: the SQP solver succeeded where all single subsystem solvers have failed.\n");
if (soltype > 0) {
Base::Console().Log("If you see this message please report a way of reproducing this result at\n");
Base::Console().Log("http://www.freecadweb.org/tracker/main_page.php\n");
}
break;
}
} // soltype
}
Base::TimeInfo end_time;
if(debugMode==GCS::Minimal || debugMode==GCS::IterationLevel){
Base::Console().Log("Sketcher::Solve()-%s-T:%s\n",solvername.c_str(),Base::TimeInfo::diffTime(start_time,end_time).c_str());
}
SolveTime = Base::TimeInfo::diffTimeF(start_time,end_time);
return ret;
}GCS::System::solve()最终完成了几何约束的求解,GCS::System::solve()提供了DogLeg、LevenbergMarquardt、BFGS、SQP(augmented system)等多种几何约束求解算法。
int System::solve(bool isFine, Algorithm alg, bool isRedundantsolving)
{
if (!isInit)
return Failed;
bool isReset = false;
// return success by default in order to permit coincidence constraints to be applied
// even if no other system has to be solved
int res = Success;
for (int cid=0; cid < int(subSystems.size()); cid++) {
if ((subSystems[cid] || subSystemsAux[cid]) && !isReset) {
resetToReference();
isReset = true;
}
if (subSystems[cid] && subSystemsAux[cid])
res = std::max(res, solve(subSystems[cid], subSystemsAux[cid], isFine, isRedundantsolving));
else if (subSystems[cid])
res = std::max(res, solve(subSystems[cid], isFine, alg, isRedundantsolving));
else if (subSystemsAux[cid])
res = std::max(res, solve(subSystemsAux[cid], isFine, alg, isRedundantsolving));
}
if (res == Success) {
for (std::set<Constraint *>::const_iterator constr=redundant.begin();
constr != redundant.end(); ++constr){
//DeepSOIC: there used to be a comparison of signed error value to
//convergence, which makes no sense. Potentially I fixed bug, and
//chances are low I've broken anything.
double err = (*constr)->error();
if (err*err > (isRedundantsolving?convergenceRedundant:convergence)) {
res = Converged;
return res;
}
}
}
return res;
}十、讨论
“好问题比(完美)答案更重要”。按照研究的深度,本文抛出以下问题供大家研究与讨论,希望对大家有帮助,也非常欢迎大家予以指教。
Q1. Part::Geometry与Part::TopoShape有什么区别?
Q2. 请梳理Sketcher工作流程:创建草图、添加几何元素、添加约束、设置几何约束求解器、求解几何约束问题、更新几何元素。
Q3. Sketcher::Constraint中First\FirstPos、Second\SecondPos、Third\ThirdPos等分别表示什么?
A3. 目前FreeCAD Sketcher模块中的约束最多支持三个几何元素。First\FirstPos、Second\SecondPos、Third\ThirdPos分别用于标定三个几何元素的ID。
前面已经说过,几何约束通常可以转换成几何点的约束。至于为什么需要采用类似First\FirstPos的一对参数来标记几何点,主要是为了防止几何点的多义性。(当FirstPos取PointPos::None,表示几何体标号为First的几何体;否则,则表示几何体First上的start/end/middle几何点。)
"A geoId is a unique identifier for geometry in the Sketch. geoId >= 0 means an index in the Geometry list. geoId < 0 refers to sketch axes and external geometry. "
"posId is a PointPos enum. PointPos lets us refer to different aspects of a piece of geometry. sketcher::none refers to an edge itself (eg., for a Perpendicular constraint on two lines). sketcher::start and sketcher::end denote the endpoints of lines or bounded curves. sketcher::mid denotes geometries with geometrical centers (eg., circle, ellipse). Bare points use 'start'. More complex geometries like parabola focus or b-spline knots use InternalAlignment constraints in addition to PointPos."
例如:在下图中,对于点b,即可以看作是L1的终点,也可以看作是L2的起点。
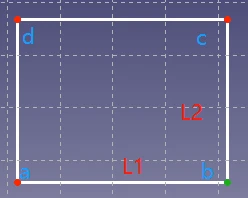
对于First\FirstPos来说:First表示几何体(点、直线、圆弧、二次曲线等)的标号geoId;FirstPos为none时,表示整个几何体First;FirstPos为start时,表示几何体First的起始点;First为end时,表示几何体的First的终点;First为middle时,表示几何体First的中点(比如对于圆弧,表示圆心)。
可以参照Sketcher::SketchObjectObject::getPoint()函数以理解这种几何元素(点)表示方法。
Base::Vector3d SketchObject::getPoint(int GeoId, PointPos PosId) const
{
if(!(GeoId == H_Axis || GeoId == V_Axis
|| (GeoId <= getHighestCurveIndex() && GeoId >= -getExternalGeometryCount()) ))
throw Base::ValueError("SketchObject::getPoint. Invalid GeoId was supplied.");
const Part::Geometry *geo = getGeometry(GeoId);
if (geo->getTypeId() == Part::GeomPoint::getClassTypeId()) {
const Part::GeomPoint *p = static_cast<const Part::GeomPoint*>(geo);
if (PosId == start || PosId == mid || PosId == end)
return p->getPoint();
} else if (geo->getTypeId() == Part::GeomLineSegment::getClassTypeId()) {
const Part::GeomLineSegment *lineSeg = static_cast<const Part::GeomLineSegment*>(geo);
if (PosId == start)
return lineSeg->getStartPoint();
else if (PosId == end)
return lineSeg->getEndPoint();
} else if (geo->getTypeId() == Part::GeomCircle::getClassTypeId()) {
const Part::GeomCircle *circle = static_cast<const Part::GeomCircle*>(geo);
if (PosId == mid)
return circle->getCenter();
} else if (geo->getTypeId() == Part::GeomEllipse::getClassTypeId()) {
const Part::GeomEllipse *ellipse = static_cast<const Part::GeomEllipse*>(geo);
if (PosId == mid)
return ellipse->getCenter();
} else if (geo->getTypeId() == Part::GeomArcOfCircle::getClassTypeId()) {
const Part::GeomArcOfCircle *aoc = static_cast<const Part::GeomArcOfCircle*>(geo);
if (PosId == start)
return aoc->getStartPoint(/*emulateCCW=*/true);
else if (PosId == end)
return aoc->getEndPoint(/*emulateCCW=*/true);
else if (PosId == mid)
return aoc->getCenter();
} else if (geo->getTypeId() == Part::GeomArcOfEllipse::getClassTypeId()) {
const Part::GeomArcOfEllipse *aoc = static_cast<const Part::GeomArcOfEllipse*>(geo);
if (PosId == start)
return aoc->getStartPoint(/*emulateCCW=*/true);
else if (PosId == end)
return aoc->getEndPoint(/*emulateCCW=*/true);
else if (PosId == mid)
return aoc->getCenter();
} else if (geo->getTypeId() == Part::GeomArcOfHyperbola::getClassTypeId()) {
const Part::GeomArcOfHyperbola *aoh = static_cast<const Part::GeomArcOfHyperbola*>(geo);
if (PosId == start)
return aoh->getStartPoint();
else if (PosId == end)
return aoh->getEndPoint();
else if (PosId == mid)
return aoh->getCenter();
} else if (geo->getTypeId() == Part::GeomArcOfParabola::getClassTypeId()) {
const Part::GeomArcOfParabola *aop = static_cast<const Part::GeomArcOfParabola*>(geo);
if (PosId == start)
return aop->getStartPoint();
else if (PosId == end)
return aop->getEndPoint();
else if (PosId == mid)
return aop->getCenter();
} else if (geo->getTypeId() == Part::GeomBSplineCurve::getClassTypeId()) {
const Part::GeomBSplineCurve *bsp = static_cast<const Part::GeomBSplineCurve*>(geo);
if (PosId == start)
return bsp->getStartPoint();
else if (PosId == end)
return bsp->getEndPoint();
}
return Base::Vector3d();
}Q4. Sketcher::Constrint::isDriving用于表示驱动约束(Driving Constraint),那么什么是驱动约束(Driving Constraint)? 什么是非驱动约束(Non-driven Constaint)?这两类约束有什么区别呢?
A4. Sketcher ToggleDrivingConstraint
FreeCAD应用:一道小学平面几何考题
Q5. 解释Sketcher::Constraint::isInVirtualSpace含义
A5. Sketcher SwitchVirtualSpace
Q6. Sketcher::Sketch中定义了Parameters、DrivenParameters、FixParameters、MoveParameters、InitParameters等参数列表,这些参数分别表示什么呢?
// solving parameters
std::vector<double*> Parameters; // with memory allocation
std::vector<double*> DrivenParameters; // with memory allocation
std::vector<double*> FixParameters; // with memory allocation
std::vector<double> MoveParameters, InitParameters;A6. 这些参数存储几何约束问题相关的不同参数,具体来说:
| 参数 | 含义 | 说明 |
| Parameters | 所有待求变量,包括驱动约束变量、非驱动约束变量。 | |
| DrivenParameters | 非驱动约束变量,参数值由其他参数确定。 | Drving Constraint 用于测量 |
| FixParameters | 固定变量,参数值已知。 | 辅助线等几何元素 |
| InitParameter | 草图中,当拖动几何元素时,记录相关几何点的初始位置 | |
| MoveParameter | 草图中,当拖动几何元素时,相关几何点的待求位置 |
Q7. 在Sketcher::SketchObject中,Geometry、Constraints、ExternalGeometry等用于存储几何约束问题相关数据;而在Sketcher::Sketch中,Geoms、Constrs、Parameters、FixParameters、Points、Lines、Arcs、Circles等存储几何约束问题数据;同样地,在GCS::System中,使用plist、pdrivenlist、pIndex、pDependentParameters、pDependentParametersGroups、clist、c2p、p2c、plists、clists等存储几何约束问题数据。
为什么Sketcher::SketchObject、Sketcher::Sketch、GCS::System都要存储几何约束问题相关的数据呢? 直接存储到GCS::System不可以吗?
A7. 笔者认为:FreeCAD Sketcher模块中,Sketcher::SketchObject、Sketcher::Sketch、GCS::System等组件均存储了几何约束问题相关数据,主要是为了通过这种三层结构来实现用户界面输入信息与底层特定约束求解器的解耦。
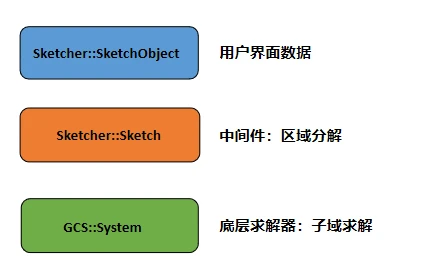
" the information flow between the user interface and the underlying core solver has been formalized by a high-level representation that is minimally com- mitted to the particular capabilities or technical characteristics of the solver, and that is independent of the interface. Such a representation can become the basis for archiving sketches in a neutral format." Ref. from Bouma 1995.
具体来说:
1. 在Sketcher::SketchObject中,Geometry、Constraints、ExternalGeometry等主要用于存储用户界面输入的几何约束问题相关数据;
2. 在Sketcher::Sketch中,Geoms、Constraints等可以看作一个中间件,实现了对Sketcher::SketchObject的输入数据转换功能;Parameters、FixParameters等存储几何约束参数变量;Points、Lines、Arcs、Circles等存储几何约束求解的结果;
3. 在GCS::System中,plist、pdrivenlist、pIndex、pDependentParameters、pDependentParametersGroups、clist、c2p、p2c、plists、clists等存储了子区域的待求变量及相关数据。
Q8. GCS::System中subSystems、subSystemsAux有什么区别?
std::vector<SubSystem *> subSystems, subSystemsAux;Q9. Sketcher默认采用DogLeg算法求解连通分量内的约束方程?试分析求解流程,并给出算法描述。
Q10. 若几何约束问题是适定的,如何改进Sketcher模块,使其解能够满足用户真正需求?
参考资料
- FreeCADWeb
- SALOME
- Sketcher tutorial
- SOLVESPACE
- openDCM
- Marriott K , Chok S S . QOCA: A Constraint Solving Toolkit for Interactive Graphical Applications. Constraints, 2002, 7(3/4):229-254.
- Jorge Nocedal. Numerical Optimization. 2006.
- 牛顿法与拟牛顿法学习笔记
- Ait-Aoudia S , Bahriz M , Salhi L . 2D Geometric Constraint Solving: An Overview[M]. IEEE, 2009.
- 杜平安. CAD/CAE/CAM方法与技术. 清华大学出版社, 2010.
- 王定标. CAD/CAE/CAM技术与应用. 化学出版社, 2010.
- 袁清珂. CAD/CAE/CAM技术. 电子工业出版社, 2010.
- 袁亚湘. 最优化理论与方法. 科学出版社, 1993.
- 欧阳应秀. 几何约束求解的BFGS-混沌混合算法. 浙江大学学报(工学版), 2005(09):60-64.
