古典密码学
已知最早使用密码学的人之一是尤利乌斯 凯撒,他通过将字母表中的字母向后平移三个单位长度来实现加密(模26的平移),我们使用数学语言描述如下。
我们使用一个枚举类型0-25来代表26个字母,使用符号Z表示,定义一个函数f,定义域为非负整数p,我们有
f(p) = (p+3) mod 26
相对地,解密的过程就是将字母向前平移三个单位实现,同样是模26计算
f^(-1)(p) = (p-3) mod 26
同理,我们在加密和解密过程中可以规定任意的平移长度,令平移长度为k,则得到
f(p) = (p+k) mod 26
f^(-1)(p) = (p-k) mod 26
下面使用c语言来描述这个加密解密过程。我们令平移长度k=3,将"HELLO"进行加密和解密
#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 10
//加密函数,返回 加密后的字符串
//注意,因为是字符是ASCII码值,所以我们在加密过程中需要进行一定的变化
char *encryption(char *str, int k, int length){
char *encoding;
for(int i=0; i<length; i++){
if(str[i]>=65 && str[i]<=90){
//大写字母
encoding[i] = ((str[i]-65)+k) % 26 + 65;
} else if(str[i]>=97 && str[i]<=122){
//小写字母
encoding[i] = ((str[i]-97)+k) % 26 + 97;
} else {
printf("error:not a letter\n");
}
}
return encoding;
}
//解密函数
char *decryption(char *str, int k, int length){
char *encoding;
for(int i=0; i<length; i++){
if(str[i]>=65 && str[i]<=90){
//大写字母
encoding[i] = ((str[i]-65)-k) % 26 + 65;
} else if(str[i]>=97 && str[i]<=122){
//小写字母
encoding[i] = ((str[i]-97)-k) % 26 + 97;
} else {
printf("error:not a letter\n");
}
}
return encoding;
}
int main(){
char *str = "HELLO";
char *c = encryption(str, 3, 5);
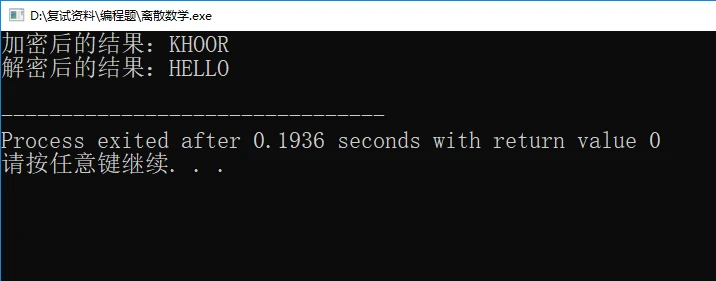
printf("加密后的结果:%s\n", c);
c = decryption(c, 3, 5);
printf("解密后的结果:%s\n", c);
return 0;
}运行的结果如下
RSA加密算法
RSA加密算法是一种非对称加密算法,当两台主机进行RSA加密通信的时候,需要一个公钥e和一个私钥d。
加密解密按照如下步骤进行:
1)找到互为素数的两个数p和q
2)令n = p*q
3)计算欧拉函数φ(n) = (p-1)*(q-1)
根据欧拉定理我们知道,任意一个与n互质的数a都有 a^n在模n计算中都与1互质
4)寻找一个公钥e,满足 1<e<φ(n) 且e与φ(n)互质
寻找一个私钥d,满足ed 除以 φ(n)的余数为1
5)假设发送方要发送的数据为m,求得 m^e 除以n的余数C,C即为要发送的加密数据
6)接收方收到数据C后,计算C^d除以n的余数,这个余数就是发送方发送的数据m
下面我们用公式描述一下加密解密的过程
![]()
![]()
![]()
由步骤4)我们得到
![]()
由(3)和(4)得到
![]()
由费米-欧拉定理得到
![]()
联立(5)(6)两式得到
![]()
化简(7)式得到
![]()
通过(8)式我们就很清晰的看到c^d除以n的余数为m
下面我们举一个RSA加密解密的例子
1)p = 43, q = 59
2)n = p*q = 2537
3)计算欧拉函数φ(n) = (p-1)*(q-1) = 2436
4)取公钥e = 13
5)取私钥d = 937 (这一步相对困难)
假设我们要发送的数据为1819 1415
我们计算C1 = pow(1819, 13) mod 2537 = 2081 C2 = pow(1415, 13) mod 2537 = 2182
发送方发送的数据为2081 2182
接收方接收到数据后解密
M1 = pow(2081, 937) mod 2537 = 1819
M2 = pow(2182, 937) mod 2537 = 1415
至此,RSA加密解密过程就完成啦
