CGA算法使用概率变量表示染色体种群,这一突出的优点使得它能够高效地通过硬件得以实现。
然而,在处理复杂问题时,它的执行效率却往往无法达到实际应用的要求。
针对这一弱点,在对标准CGA进行了深入分析与研究后,提出了一种带有收敛趋势性的CGA算法,称之为TCGA算法(Compact Genetic Algorithm with Tendency)。
所提出的新算法作为标准CGA算法的一种变体,其旨在提高演化算法在解决实际问题时对问题解空间的搜索能力和演化算法的收敛速度。
TCGA算法在保持了标准CGA算法易于硬件实现等优点的同时,有效地提高了演化算法的收敛速度,是一种更为有效,并且适用于更多的实际应用的演化算法。
在研究过程中,通过使用不同类型的测试函数分析TCGA算法的性能,并且将测试结果与标准CGA算法的演化结果进行比较,比较结果表明,TCGA算法的收敛速度和最优解的质量都得到了提高,比标准CGA算法更适合于实际演化硬件的应用。
TCGA算法原理
尽管标准CGA算法有着便于硬件实现的优点,但是它只适用于解决规律性较为明显的简单问题,对于略为复杂的问题其很容易发生早熟收敛现象。
另外,在概率变量收敛之前,标准CGA算法经常会丢失所获得的优秀个体。
最为关键的是,对于演化硬件的实际应用缺少足够的搜索能力。
TCGA算法在标准CGA的基础上,主要进行了两方面的改进。
一方面是,在算法中增加了当前解朝向最优解的趋势性的判断,以促进概率变量的更新能够在每一步都逐渐地接近最优解。
具体做法为,在每一代的演化过程中,对于染色体个体的每一位,首先对其进行反转,然后判断比较每一位反转后的个体与原个体之间的适应度值。当新个体的适应度值更大时,再判断反转位的值,如果该位进行反转后的值为1,则通过增加1/N的步长来更新该位所对应的概率变量值;如果该位进行反转后的值为0,则通过减少1/N的步长来更新该位所对应的概率变量值。
依靠此种对于收敛趋势的判断,可以增加算法的搜索能力使得染色体个体能够更快地收敛到最优解。
另一方面,引入了改进的变异操作。传统的变异操作是随机性的,并且使用一个概率值来控制变异。
TCGA算法在传统的随机变异方法的基础上,增加了新的变异步骤,通过判断染色体个体的每一位的概率变量值决定是否对候选染色体个体的相应位执行变异操作。
判断的标准为,如果概率变量值大于0.5,且当前位为0则反转该位,为1则该位保持不变;否则当前位为1则反转该位,为0则该位保持不变。
通过引入改进的变异操作,能够以更大的机率得到更好的染色体个体,并且保持演化过程中种群的多样性,从而避免了局部收敛状况的发生。
TCGA 算法的伪码如下所示:
Step.1 Initialize the probability vector-L is the number of bits in the genome.
for i:=1 to L do p[i]:=0.5; ------P为概率变量
Step.2 Generate two initial individuals from the vector.
a:=generate(p);
b:=generate(p);
Step.3 Let them compete.Here resamp_rate is champion resampling frequency.
[winner, loser]:=evaluate(a,b,resamp_rate); ------增加“冠军重采样”策略
Step.4 Update the probability vector toward the better one.
Here we judge each bit of vector using the tendence criterion.
for i:=1 to L do ------L为染色体个体位串长度
w:=winner;
if winner[i] <> loser[i] then
if winner[i]= =1 then { w[i]:=0; ------增加收敛趋势性判断
fw:=fitness(w);
if fw>fwn then p[i]:=p[i]-1/N; ------1/N为概率值更新步长
else p[i]:=p[i]+1/N; }
else { w[i]:=1;
fw:=fitness(w);
if fw>fwn then p[i]:=p[i]+1/N;
else p[i]:=p[i]-1/N; }
a) Mutate and substitute.
if winner= =a then { c:=mutate(a); ------引入改进的变异操作
if fitness(c)>fitness(a) then a:=c; }
else { c:=mutate(b);
if fitness(c)>fitness(b) then b:=c; }
b) Generate one individual from the updated vector.
if winner= =a then b:=generate(p); ------增加精英保留策略
else a:=generate(p);
Step.5 Check the stopping criterion.
for i:=1 to L do
if p[i]>0 and p[i]<1 then goto step.3.
Step.6 The final probability vector represents the solution.TCGA算法仿真分析
为了验证TCGA算法的性能,对算法进行软件仿真,使用四种不同类型的测试函数对算法的收敛性进行测试,同时将所得到的测试结果与使用相同测试函数对标准CGA算法的测试结果相比较。
1) Onemax函数
该测试函数为Onemax函数,其计算公式为:

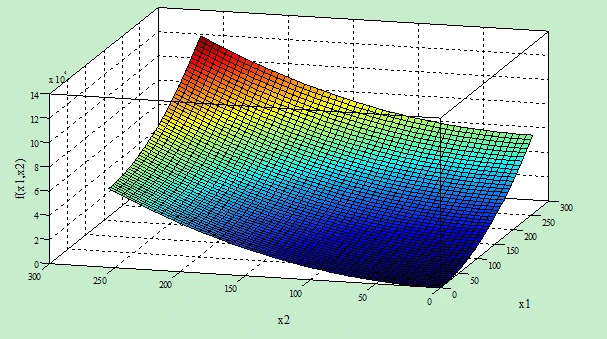
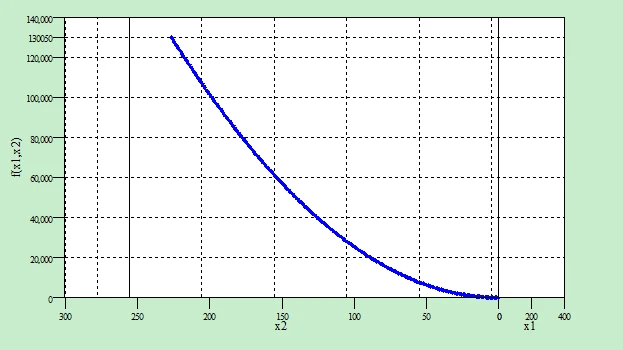
它在定义域[0,255]内为单调递增函数,其曲面图及剖面图如下图所示,且具有惟一全局极大值130050。
Onemax函数曲面示意图
Onemax函数剖面示意图
对于该测试函数,使用TCGA算法仅需要一代演化运行即可收敛到全局极大值,与之相比,使用标准CGA算法则需要运行4000代。
两种算法的收敛性仿真测试结果如下图所示,图中横坐标为演化代数,纵坐标为每一代最优个体的适应度值。
TCGA收敛性仿真测试图
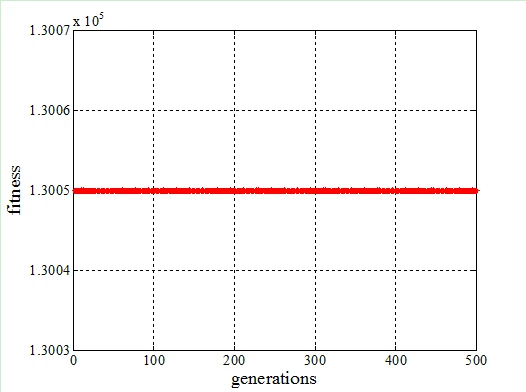
标准CGA收敛性仿真测试图
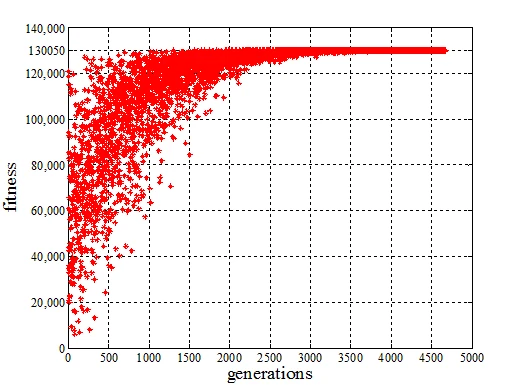
2) One-order振荡函数
该测试函数为一元的振荡函数,其计算公式为:
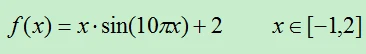
它在定义域[-1,2]内呈现振荡特性,具有多个局部极大值,其曲线图如下图所示。
通过使用对函数进行求导计算极值的方法,可以得出该函数在定义域内的惟一全局极大值略大于3.85。
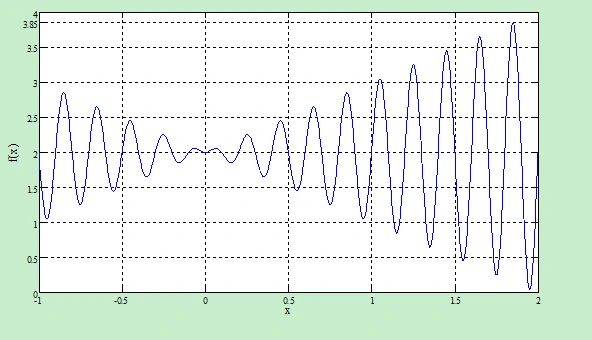
对于该测试函数,使用TCGA算法进行演化,函数收敛到全局极大值所需要的演化代数在500代以内,而使用标准CGA算法需要超过4000代的演化次数函数才能够收敛,并且收敛结果为局部极大值,呈现早熟收敛现象。
两种算法的收敛性仿真测试结果如下图所示,图中横坐标为演化代数,纵坐标为每一代最优个体的适应度值。
TCGA收敛性仿真测试图
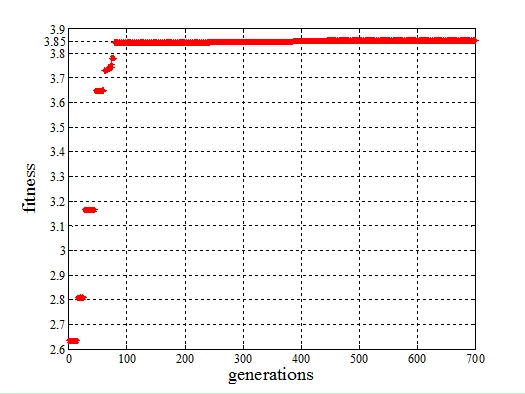
标准CGA收敛性仿真测试图
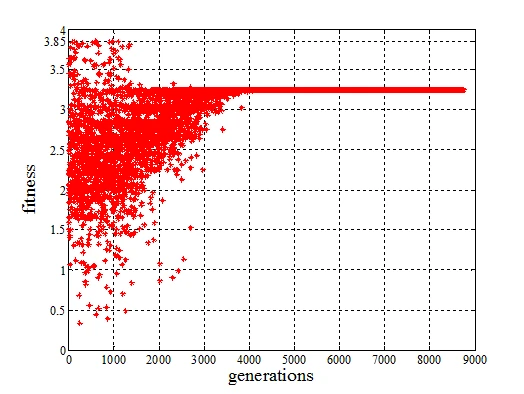
从仿真测试结果中可以看出,由于标准CGA算法并未采用精英保留策略,在每一代的演化开始时,都需要依据当前的概率变量值重新生成两个新个体。
因此,虽然算法曾经在演化过程中搜索得到定义域内的全局极大值,但是最后却仍然按照每一代演化所更新的概率变量值收敛到局部极大值点,以致于出现早熟收敛现象。
3) 固定目标位串的演化
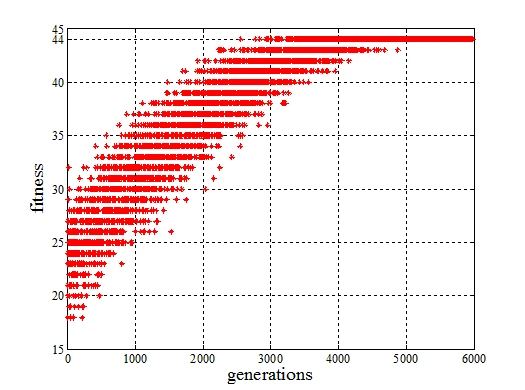
该测试部分对固定的目标位串进行演化,目标位串的长度为44,以候选位串和目标位串的相同位的数目作为适应度评估函数,当适应度值达到最大值时,所得到的位串即为需要演化的目标位串。
测试所选用的目标位串如下:
11000101100001010111110111100101101110011011
对于该测试部分,使用TCGA算法,候选位串仅仅经过几十代的演化即可收敛到目标位串。
而使用标准CGA算法,虽然最终也可令候选位串收敛到目标位串,但是其所耗费的时间远远大于TCGA算法。
两种算法的收敛性仿真测试结果如下图所示,图中横坐标为演化代数,纵坐标为每一代最优个体的适应度值。
TCGA收敛性仿真测试图
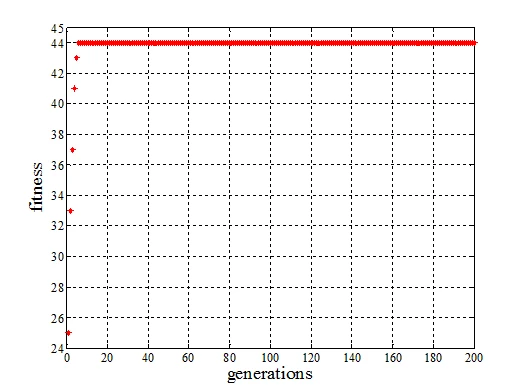
标准CGA收敛性仿真测试图