定点加减运算
补码加减法
数用补码表示,符号位参见运算
原码乘法 :
乘法规则
操作数、结果用原码表示;
绝对值运算,符号单独处理;
被乘数(B)、累加和(A)取双符号位;
乘数末位(Cn)为判断位,其状态决定下部操作;
做N次循环(累加、右移) ;
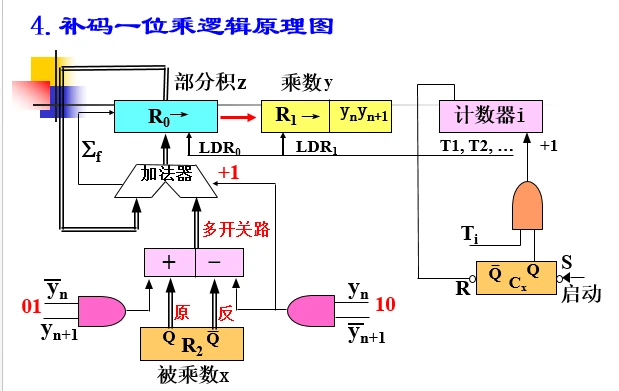
定点补码一位乘法
1、A、B 取双符号位,符号参加运算;
2、 C取单符号位,符号参见移位,以决定最后是否修正;
3、 C末位设置附加位Cn+1 ,处置为0 ,CnCn+1 组成判断位,决定运算操作;
4 、 作 n步循环,若需作第n+1步,则不移位,仅修正。
补码加法
[ x ]补+[ y ]补=[ x+y ]补 (mod 2)
特点:不需要事先判断符号,符号位与码值位一起参加运算。
符号位相加后若有进位,则舍去该进位数字。
在模2意义下,任意两数的补码之和等于该两数之和的补码。
这是补码加法的理论基础。
例: x=0.1001, y=0.0101, 求 x+y。
解: [x]补=0.1001, [y]补=0.0101
[x]补 0.1001
+ [y]补 0.0101
[x+y ]补 0.1110
例: x=+0.1011, y=-0.0101, 求 x+y。
解: [x]补=0.1011, [y]补=1.1011
[x]补 0.1011
+[y]补 1.1011
[x+y]补 10.0110补码减法
补码减法运算的公式:
[ x-y ]补=[ x ]补-[ y ]补=[ x ]补+[-y ]补
例: x=+0.1101, y=+0.0110, 求 x-y。
解: [x]补=0.1101
[ y]补=0.0110, [-y]补=1.1010
[x]补 0.1101
+[-y]补 1.1010
[x-y]补 10.0111
x-y=+0.0111
例: x= -0.1101,y= -0.0110,求x-y=?
解: [x]补=1.0011
[y]补=1.1010 [-y]补=0.0110
[x]补 1.0 0 1 1
+ [-y]补 0.0 1 1 0
[x-y]补 1.1 0 0 1
∴x–y = -0.0111
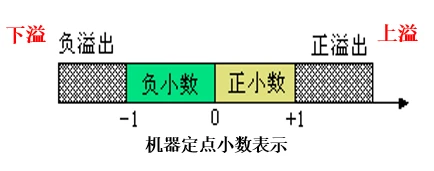
- 溢出及与检测方法
在定点小数机器中,数的表示范围为|x|<1。在运算过程中如出现大于1的现象,称为 “溢出”。
例: x=+0.1011, y=+0.1001, 求x+y。
解: [x]补=0.1011 [y]补=0.1001
[x]补 0. 1 0 1 1
+ [y]补 0. 1 0 0 1
[x+y]补 1. 0 1 0 0
两个正数相加的结果成为负数,这显然是错误的。
例: x= -0.1101, y= -0.1011, 求x+y。
解: [x]补=1.0011 [y]补=1.0101
[x]补 1. 0 0 1 1
+ [y]补 1. 0 1 0 1
[x+y]补 0. 1 0 0 0
两个负数相加的结果成为正数,这同样是错误的。
发生错误的原因,是因为运算结果产生了溢出。
两个正数相加: 结果大于机器所能表示的最大正数,称为上溢;
两个负数相加:结果小于机器所能表示的最小负数,称为下溢。
2.溢出的检测方法
[x]补 0. 1 0 1 1
+ [y]补 0. 1 0 0 1
[x+y]补 1. 0 1 0 0
[x]补 1. 0 0 1 1
+ [y]补 1. 0 1 0 1
[x+y]补 0. 1 0 0 0
(2) 双符号位法
一个符号位只能表示正、负两种情况,当产生溢出时,符号位的含义就会发生混乱。如果将符号位扩充为两位(Sf1、Sf2),其所能表示的信息量将随之扩大,既能判别是否溢出,又能指出结果的符号。
双符号位的含义如下:
Sf1Sf2 = 00 结果为正数,无溢出
01 结果正溢
10 结果负溢
11 结果为负数,无溢出
即:结果的两个符号位的代码不一致时,表示溢出;
两个符号位的代码一致时,表示没有溢出。
不管溢出与否,最高符号位永远表示结果的正确符号。
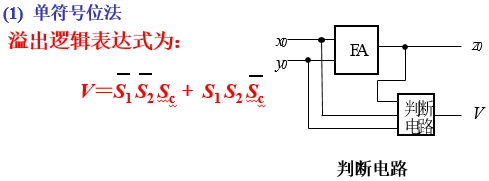
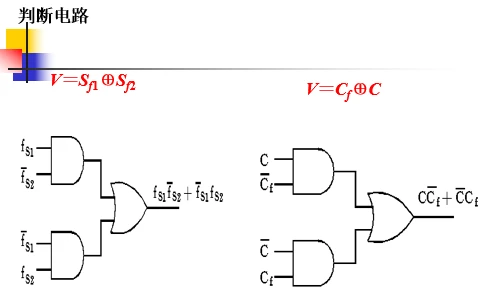
溢出逻辑表达式为: V=Sf1⊕Sf2
中Sf1和Sf2分别为最高符号位和第二符号位,此逻辑表达式可用异或门实现。
例 x= +0.1100, y= +0.1000, 求x+y。
解: [x]补=00.1100 [y]补=00.1000
[x]补 0 0. 1 1 0 0
+ [y]补 0 0. 1 0 0 0
0 1. 0 1 0 0
符号位出现“01”,表示已溢出,正溢。即结果大于+1
例 x= -0.1100, y= -0.1000, 求x+y。
解: [x]补=11.0100 [y]补=11.1000
[x]补 1 1.0 1 0 0
+ [y]补 1 1.1 0 0 0
1 0. 1 1 0 0
符号位出现“10”,表示已溢出,负溢出。即结果小于-1
(3) 利用进位值的判别法
[x]补 0 0. 1 1 0 0
+[y]补 0 0. 1 0 0 0
0 1. 1 0 0 0
[x]补 1 1.0 1 0 0
+[y]补 1 1.1 0 0 0
1 0.1 1 0 0
从上面例中看到:
当最高有效位有进位而符号位无进位时,产生上溢;
当最高有效位无进位而符号位有进位时,产生下溢。
(简单地说是正数相加为负数或负数相加为正数则产生溢出)
故溢出逻辑表达式为: V=Cf⊕Co
其中Cf为符号位产生的进位,Co为最高有效位产生的进位。此逻辑表达式也可用异或门实现。
- 3.3 定点乘法运算
- 乘法的手工算法
设n位被乘数和乘数用定点小数表示
被乘数 [x]原=xf . xn-1… x1x0
乘数 [y]原=yf . yn-1… y1y0
则乘积
[z]原=(xf⊕yf)+(0. xn-1… x1x0)(0. yn-1… y1y0)
式中,xf为被乘数符号,
yf为乘数符号。
(1)乘积符号的运算规则:同号相乘为正,异号相乘为负。
(2) 手工运算过程:
设x=0.1101,y=0.1011
0. 1 1 0 1 (x)
0. 1 0 1 1 (y)
1 1 0 1
1 1 0 1
0 0 0 0
- 1 1 0 1
- 1 0 0 0 1 1 1 1 (z)
一般而言,设被乘数x,乘数y都是小于1的n位定点正数:
x=0.x1x2……xn <1
y=0.y1y2……yn <1
其乘积为:
x·y=x(0.y1y2……yn )
=x(y12-1 +y22-2 +…+ yn2-n )
= 2-1(y1x+2-1(y2x+2-1(…+2-1(yn-1x+2-1(ynx+0))…)))
- 乘法的手工算法
形成递推公式
令zi表示第i次部分积,则根据从内到外的原则有:
z0 = 0,
z1 = 2-1(ynx+z0)
z2 = 2-1(yn-1x+z1)
┊
zi = 2-1(yn-i+1x+zi-1)
┊
zn = xy = 2-1(y1x+ zn-1)
特点:每次只需要相加两个数,然后右移一位。且相加的两个数(部分积和位积)都只有n位,因而不需要2n位的加法器。
3.原码一位乘法流程图
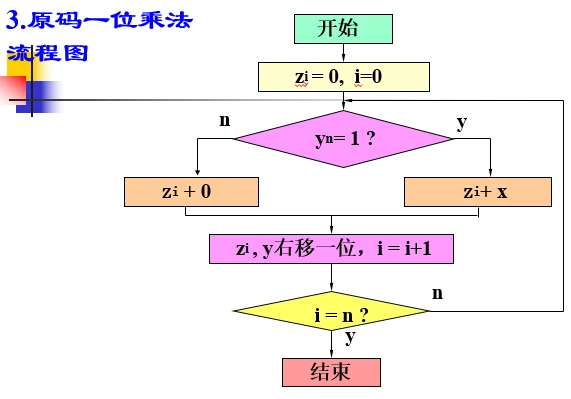
例:x=0.1101 , y=0.1011 , 求 x·y 。

4.原码一位乘硬件逻辑原理图
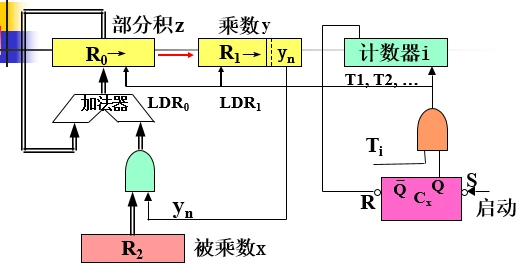
计数器:对移位的次数进行计数,以便判断乘法运算是否结束。
当计数器i=n时,计数器i的溢出信号使控制触发器Cx
置0,关闭时序脉冲T,乘法操作结束。
2 补码一位乘法
1.原码一位乘的缺点
原码一位乘法的主要问题是:符号位不能参与运算,
而补码乘法可以实现符号位直接参与运算。
二是对于采用补码存储的机器,从存储器中取出的是操作数的补码,需先将其转换成原码,这样很不方便,而且影响速度。
2.补码一位乘法的规律推导
(1)真值和补码之间的关系
设[x]补 = x0.x1x2…xn
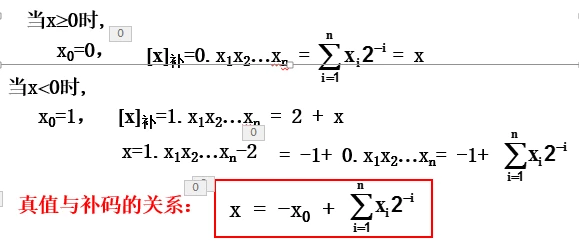
(2) 补码的右移
在补码机器中,一个数不论其正负,连同符号位向右移一位,符号位保持不变,就等于乘1/2。
设 [x]补 = x0.x1x2…xn

(3) 补码乘法规则

1)、当被乘数x符号任意,乘数y符号为正时:
根据补码定义:



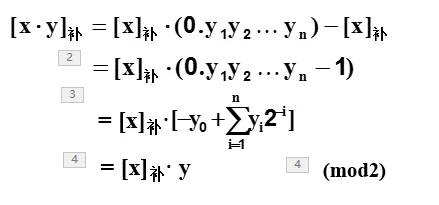


2)、 当被乘数x符号任意,乘数y符号为负时:
定点数二位乘法
乘数每两位的取值情况,一次求出对应于该两位的部分积。此时,只要增加少量逻辑电路,就可使乘法速度提高一倍。
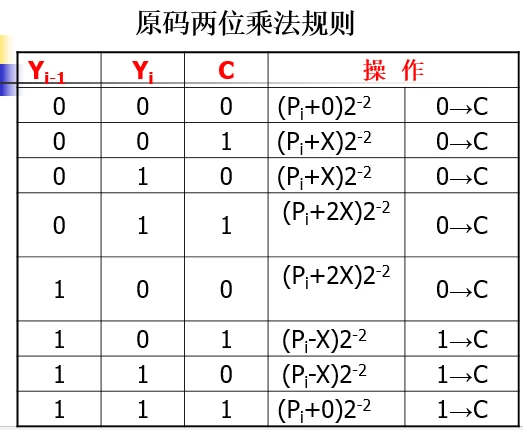
1. 原码两位乘
乘数和被乘数都用原码表示。
两位乘数有四种可能组合,对应于以下操作:
00——相当于0·X。部分积Pi右移2位;
01——相当于1·X。部分积Pi+X,右移2位;
10——相当于2·X。部分积Pi+2X,右移2位;
11——相当于3·X。部分积Pi+3X, 右移2位。
例 假定X=0.100111,Y=0.100111
则:[-X]补=1.011001
X·Y=0.010111110001
如果最后一次操作欠下+4X,则最后一次右移2位后还需补充+X操作,+X后不再移位 。
补码两位乘
根据前述的布斯算法,将两步合并成一步,即可推导出补码两位乘的公式。假设上一步的部分积为[Pi]补,本步的部分积应为:
[Pi+1]补={[Pi]补+(Yn-i+1-Yn-i)·[X]补}2-1
下一步的部分积应为:
[Pi+2]补={[Pi+1]补+(Yn-i-Yn-i-1)·[X补]}2-1
将前一个公式中的[Pi+1]补代入[Pi+2]公式中:
补码两位乘
- 列表内容
