一、SGD
1、随机梯度下降算法存在的问题之一,在形如下图:
在沿着X方向上移动时,损失函数的变化会很小但对Y轴方向上的变化会比较敏感,对像这种函数,SGD的表现为:
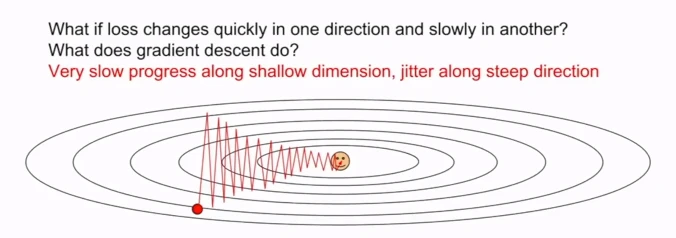
会得到这种'之'字形的过程,其原因是这类函数的梯度与最小值并不是成一条直线,导致会不断的来回波动,并且在X方向上的移动会很缓慢,这不是我们所希望的。并且这种情况在高维空间更加的普通,在神经网络中,参数的数量是非常巨大的,也就意味着有高维的参数空间,有不同的运动方向。
2、SGD的另一个问题是局部极小值点和鞍点。
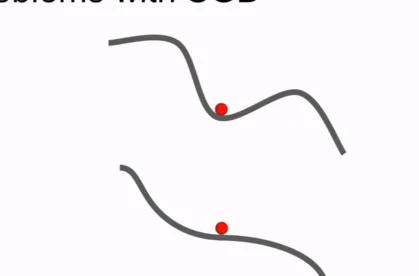
当SGD找到局部极小值点时,因为此时的梯度为0,所以此时损失函数不再变化,被卡在这里。同时当SGD找到鞍点时,梯度仍然为0,也不再移动。局部极小值看起来是一个很大的问题,但在实际中,在高维参数中,鞍点时一个非常普遍的情况。在一亿个参数的空间,鞍点 意味着损失函数在某些方向上会增加,某些方向上会减少,在高维空间中这会发生的非常频繁。但在局部极小值点中,沿任何一个方向,损失函数都会增加。
二、SGD+Momentum
1.SGD+Momentum
为了解决这个问题,提出给SGD加上一个动量向,这就是SGD+Momentum。
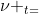
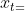
它的原理很简单,把原来的速度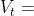 乘上一个摩擦系数
乘上一个摩擦系数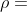 进行衰减,通常摩擦系数选择0.9再加上梯度,同时不再是往梯度方向上移动,而是沿着新的速度向量方向移动。
进行衰减,通常摩擦系数选择0.9再加上梯度,同时不再是往梯度方向上移动,而是沿着新的速度向量方向移动。
加上动量后的SGD的表现可以想象一下,假设有一个小球从山顶往下滚,球的速度会在下降时增加它的速度,那么在遇到鞍点或者局部极小值时,虽然此时没有梯度,但是球可能任然有速度,那么球就有可以冲过他们的可能,而不是卡在那里。
当拥有速度后,像'之'字形的移动会很快的抵消,减少在敏感方向上的移动,并且X方向上的速度会逐渐的增加,使X方向上的移动加快,在加上动量后能很好的解决SGD存在的问题。
2.SGD+Nesterov Momentum
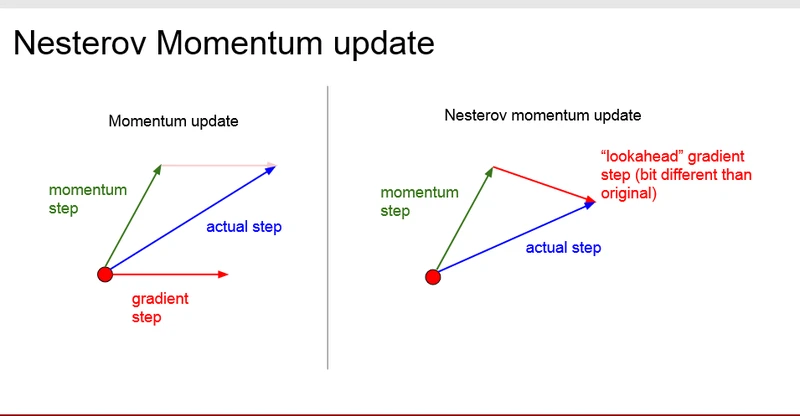
传统的Monmentum取当前位置的梯度,再与速度向量相加生成新的前进向量,而Nesterov momentum 则是在令当前位置加上速度向量后求取梯度,再回退到原来的位置,然后把梯度和速度向量相加生成新的前进向量,再与当前位置相加。
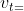
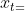 (其实在这里的式子里我是有一点疑问的,
(其实在这里的式子里我是有一点疑问的,
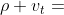 应该是加上
应该是加上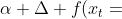 的,所以
的,所以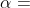 为负数?并且
为负数?并且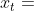 应该是减去
应该是减去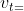 ,所以
,所以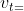 整个为负数?那么
整个为负数?那么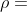 应该为负数而
应该为负数而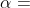 为正数?)
为正数?)
在利用SDG时,我们通常都会同时计算当前位置的梯度和损失函数,而Nesterov Momentum却要计算加上速度后的梯度,这带了不便,于是对式子进行优化。
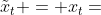
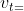
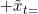
三、AdaGrad
另一种常见的优化策略是AdaGrad,它在训练过程中一直累加梯度的平方和,然后再更新时把步长除以这个平方和

(加上1e-7是为了避免平方和项为0)
那么这么做的好处在于,假设在二维参数空间,X方向的梯度小,而Y方向的梯度大,那么经过累加梯度的平方和后,梯度小的方向的平方和就会小,而梯度大的方向的平方和就会大,那么把步长除以这个平方和时,梯度大方向的维度的学习速度就会变小而梯度小的维度方向的学习速度就会加快。
随着时间的增加,梯度平方和会越来越大,而步长会越来越小,在凸优化情况下,这个特征的效果很好,在逼近最小值点时减小步长,逐渐慢下来知道收敛。但在非凸优化问题时,如果遇到局部极小值点时,就会被困住。
四、RMSProp
针对AdaGrad存在的问题,提出了RMSProp。在RMSProp,仍然计算梯度的平方和,但不只是简单的累加梯度的平方和,而是另梯度平方和按照一定的比例下降,即把梯度平方和乘以衰减率,然后把(1-衰减率)*当前位置的梯度平方再相加。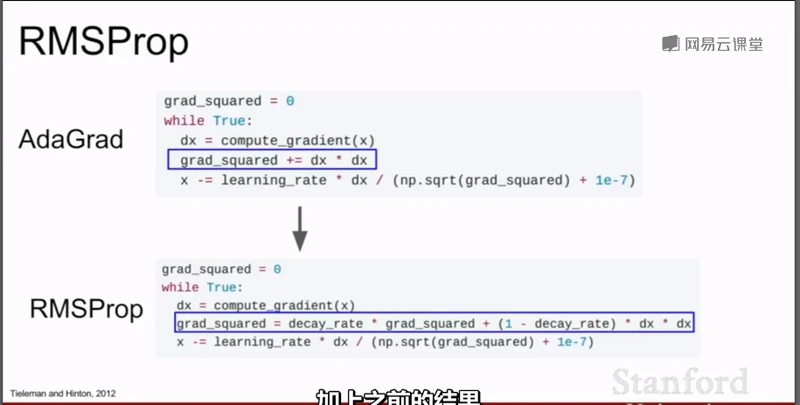
五、Adam
Adam是把带动量的SDG和RMSProp结合起来,在这里我们计算两个动量,第一动量就是速度,而第二动量是梯度的平方和。

但同时也存在一个问题, 因为一开始时,第一和第二动量都被初始化为0,那么在最初的训练 时,他们的值都会很小,一个很小的值除以一个很小的值,可能会相互抵消,也可能会导致一个很大的步长,那么就对动量进行修正。
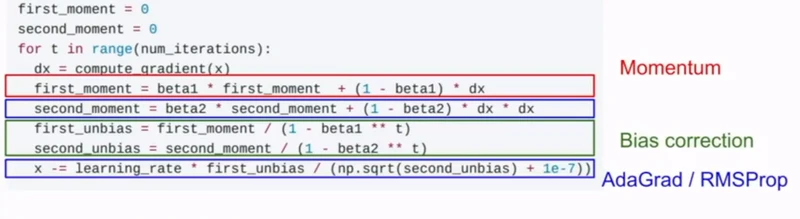
t表示时间。
通常把beta1=0.9,beta2 = 0.999,然后learning_rate = 1e-3 or 1e-4