元结构:大型异构信息网络中的相关性计算
摘要
异构信息网络(HIN)是一种图形模型,其中对象和边用类型进行注释。大型复杂的数据库,比如Y AGO和DBLP,可以建模为HINs。HINs中的一个基本问题是计算两个HIN对象之间的接近度或相关性。相关性度量可用于各种应用,包括实体解析、推荐和信息检索。一些研究已经研究了使用HIN信息进行相关性计算,然而,大多数研究只利用简单的结构,如路径,来衡量对象之间的相似性。在本文中,我们建议使用元结构来度量对象之间的接近度,元结构是对象类型的有向无环图,边缘类型连接在它们之间。元结构的优势在于它可以描述两个HIN对象之间的复杂关系(例如,DBLP的两篇论文拥有相同的作者和主题)。我们开发了三个基于元结构的相关性度量。由于这些措施的计算复杂性,我们进一步设计了一种算法,并提出了支持其评估的数据结构。我们在Y AGO和DBLP的大量实验表明,基于元结构的相关性比最先进的方法更有效,并且可以有效地计算。
1.介绍
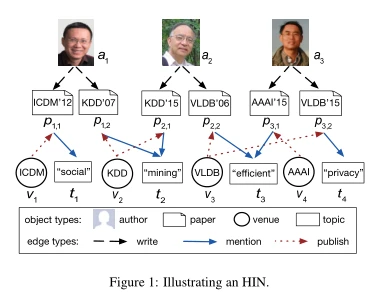
异构信息网络(HINs),如DBLP [8],Y AGO [15],DBpedia [1]和Freebase [2],最近受到了很多关注。这些图形数据源包含大量相互关联的事实,它们被用来促进有趣知识的发现[5,7,12,13]。图1展示了一个HIN,它描述了不同类型实体之间的关系(例如,作者、论文、地点和主题)。例如,韩家玮(a2)写了一篇VLDB论文(p2,2),其中提到了“高效”(t3)这个话题。给定两个HIN对象a和b,评估它们的相关性是至关重要的。这量化了a和b之间的接近程度。在图1中,简培(a1)和韩佳玮(a2)具有较高的相关性分数,因为他们都在同一个地点(KDD)发表了带有关键词“挖掘”的论文。相关性在信息检索、推荐和聚类中得到应用[18,22]:研究人员可以检索与DBLP的主题和地点高度相关的论文;在YAGO,关联性有助于提取与特定导演关系密切的演员。作为另一个例子,在实体解析应用中,具有高相关性分数的重复的HIN对象对(例如,HIN中的两个不同对象指的是同一真实世界的人)可以被识别并从HIN中移除。
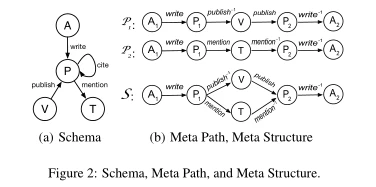
前期作品。为了度量两个图形对象之间的相关性,提出了基于邻域的度量,如公共邻居和雅克卡系数[9]。基于对象间随机游走的其他图论度量包括个性化页面排名[3]和SimRank [6]。这些度量不考虑HIN中的对象和边缘类型信息。为了处理这些信息,最近提出了元路径的概念[7,18]。元路径是一系列对象类型,中间是边类型。图2(b)展示了P1的元路径,它指出两个作者(A1和A2)通过他们在同一地点的出版物而相关联(五)。另一个元路径p2说两个作者写了包含相同主题(T)的论文。基于元路径,已经提出了几个相关度量,例如路径计数、路径模拟和路径约束随机漫步(PCRW) [7,18]。这些措施已被证明比那些不考虑对象和边缘类型信息的措施更好。
元结构。我们提出了一个新的概念,称为元结构,来描述两个图形对象之间的关系。这本质上是一个对象和边类型的有向无环图。图2(b)说明了一个元结构S,它描述了如果两个作者在同一个地点发表了论文,并且也提到了同一个主题,那么他们是相关的。元路径(例如,P1或P2)是元结构的特殊情况。然而,一个元路径不能捕捉这样复杂的关系,而这种关系可以通过一个元结构方便地表达(例如,S)。我们的实验还表明元结构比元路径更有效。
我们为元结构提供了一个合理的定义。这并不简单,因为元结构可能很复杂。然后我们提出了三个基于元结构的相关性度量。计算相关性的方式各不相同。给定一个元结构S,StructCount计算匹配S的子图的数量;结构约束子图扩展(SCSE)模拟了S约束下的子图扩展过程;有偏结构约束子图展开是结构计数和SCSE的推广。
这些新措施的一个挑战是它们的高计算成本。一般来说,评估这些度量需要在HIN上进行子图匹配操作。在一个典型的包含数百万个对象和边的HIN(例如,Y AGO)中,这可能非常昂贵。此外,应用程序(例如,集群)可能需要计算许多对象对的相关性。因此,重要的是要确保这些相关性措施能够得到有效评估。为了应对这一挑战,我们设计了一种具有两种数据结构的递归遍历算法(称为Compressed-ETree和i-LTable),以提高相关性计算的效率。
为了验证我们的方法,我们在YAGO和DBLP进行了广泛的实验。结果表明,我们的三种元结构度量在表达相关性方面比基于元路径的方法更有效。我们的算法还使元结构相关的高级变得高效,产生与元路径度量相似的运行时成本。
本文其余部分如下。我们在第2节中描述了HIN模型并总结了现有的基于元路径的方法。我们在第3节中介绍了元结构。然后我们在第4节中定义了基于元结构的相关性度量。在第5节中,我们开发了一个递归算法和两个数据结构来帮助计算相关性度量。第6节介绍了我们的实验结果。我们在第7节结束了我们的研究。
2.HIN和元路径
现在让我们回顾一下2.1节中的HIN模型。然后,我们在第2.2节总结了现有的元路径方法。
2.1 HIN模型
文献[18]中提出的一种异构信息网络(HIN),是一个有向图G = (V,E),其中有一个对象类型映射函数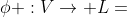 和一个链接类型映射函数
和一个链接类型映射函数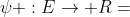 ,其中每个对象v ∈ V属于一个对象类型
,其中每个对象v ∈ V属于一个对象类型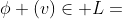 ,每个链接e ∈ E属于一个链接类型
,每个链接e ∈ E属于一个链接类型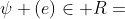 .
.
图1说明了一个HIN,它也是一个参考书目网络。论文对象可以链接(或被链接)到其作者、地点及其相关主题。请注意,两个对象之间可能存在不同类型的多条边。
定义1。HIN模式[18]。给定一个具有映射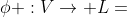 和
和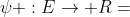 的HIN G = (V,E),其模式
的HIN G = (V,E),其模式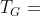 是在对象类型L和链接类型R上定义的有向图,即
是在对象类型L和链接类型R上定义的有向图,即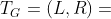 。
。
HIN模式表达了对象类型之间所有允许的链接类型。图2(a)显示了图1中定义的HIN的模式,其中节点A、P、T和V分别对应于作者、论文、主题和地点。模式中还有不同的边缘类型,如“发布”和“写入”。
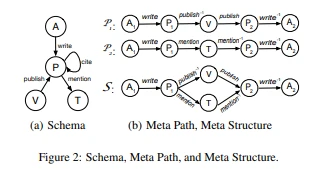
2.2 元路径
由P表示的元路径[18]本质上是在HIN模式TG上定义的路径,源对象和目标对象的类型位于路径的两端。例如,基于图2(a)中的模式,一个元路径APVPA(图2(b)中的P1)描述了在同一地点发表论文的两个作者(源对象和目标对象)之间的关系。图1的HIN中元路径的一个实例是a1→ p1,2→ t2→ p2,1→ a2。这里我们用小写字母(如v1)表示HIN中的对象,用大写字母(如V)表示对象类型。
给定一个源对象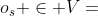 、一个目标对象
、一个目标对象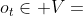 和一个元路径P,已经提出了元路径相关性度量来评估
和一个元路径P,已经提出了元路径相关性度量来评估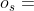 和
和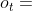 之间的相关性:
之间的相关性:
- 路径计数[18]:连接
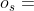 和
和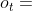 的P的元路径实例的数量。
的P的元路径实例的数量。 - PathSim [18]:路径计数的规范化版本,其值介于0和1之间。
- PCRW [7]:从
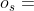 开始限制在P上的随机行走到达
开始限制在P上的随机行走到达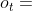 的概率。
的概率。
研究人员最近研究了元路径在搜索和挖掘任务中的使用,包括top-k搜索[18]、链接预测[16、17、20]、聚类[4、19]和推荐[10、11、21]。正如在[18]中指出的,元路径可以由熟悉HIN模式的专家提供。最近,已经提出了元路径发现算法[12],其中用户提供源和目标对象的实例,基于这些实例自动导出元路径。
元路径的缺点。虽然元路径在不同的应用程序中很有用,但是它们只能表达源对象和目标对象之间的简单关系。如图2(b)所示,两个作者之间的复杂关系不能通过他们之间的路径来捕捉。为了解决这个问题,一个简单的方法是将S分解成两个元路径(即P1和P2)。分别为P1和P2计算两个给定作者对象的相关性函数,然后基于S的相关性是基于P1和P2的相关性的线性组合[7,10,12]。然而,这种简单的方法忽略了S中的一些节点(例如P1)被两条或多条边共享的问题;将S分解成两个独立的元路径会导致这些信息的丢失。在本例中,S中的节点P1指的是一张纸。但是,当S被分解时,元路径p1a和p2a中对应的P1节点可以表示不同的论文。这会产生不准确的相关性结果。如表1所示,使用线性组合方法,现有的元路径度量将对(a2,a1)和(a2,a3)视为具有相同的相关性分数。事实上,(1)a1和a2有论文(KDD007和KDD015)都提到了“采矿”,并在KDD会场发表;(2)a2和a3的论文没有一篇是在同一个地点发表的,也没有相同的主题。因此,(a2,a1)应该比(a2,a3)具有更高的相关性分数。线性组合方法无法识别这些差异,并错误地给出了(a2,a1)和(a2,a3)的相同相关性。这需要一个更好的方法来处理这种复杂的关系,如下所述。
3.元结构
元结构设计用于捕捉两个HIN对象之间的复杂关系,定义如下。
定义2。元结构。元结构S是一个有向无环图(DAG),具有单个源节点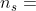 (即,入度为0)和单个接收器(目标)节点
(即,入度为0)和单个接收器(目标)节点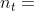 (即,出度为0),定义在HIN模式
(即,出度为0),定义在HIN模式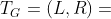 上。通常,
上。通常,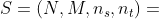 ,其中N是一组节点,M是一组边。对于任意节点 x∈ N,x∈L;对于任何链接(x,y) ∈ M,(x,y) ∈ R。
,其中N是一组节点,M是一组边。对于任意节点 x∈ N,x∈L;对于任何链接(x,y) ∈ M,(x,y) ∈ R。
图2(b)显示了一个元结构的示例。我们可以看到,S是一个DAG,源节点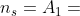 (in度0),目标节点
(in度0),目标节点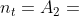 (out度0)。在定义2中,元结构有一个源节点和一个目标节点。否则,至少存在一个节点v,因此没有从
(out度0)。在定义2中,元结构有一个源节点和一个目标节点。否则,至少存在一个节点v,因此没有从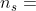 到
到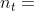 的路径通过v。由于v不影响
的路径通过v。由于v不影响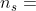 和
和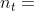 之间的关系,v可以从S中移除。
之间的关系,v可以从S中移除。
定义3。元结构的实例。给定一个HIN G和元结构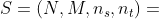 ,G上元结构S的一个实例S是G的一个子图,用
,G上元结构S的一个实例S是G的一个子图,用 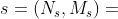 表示,这样
表示,这样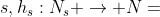 就存在一个满足以下约束的映射:
就存在一个满足以下约束的映射:
- 对象对应:对于任意对象v ∈ Ns,其对象类型φ(v)= hs(v);
- 链接对应:对于任何链接(u,v)∞(/∞)Ms,我们都有(hs(u),hs(v))∞(/∞)m。
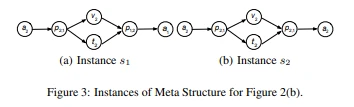
图3展示了图2(b)中元结构的两个实例,其中两种情况下的 。
。
构建元结构。在本文中,我们假设给出了元结构。我们概述了几种可以用来定义元结构的可能解决方案;他们的细节留待将来工作。
- 开发一个图形用户界面,提供绘图工具,以方便指定元结构。
- 使用现有的图形查询。例如,SPAQRL [14]是一种允许表达查询图的RDF语言。因为元结构也可以被指定为查询图,所以SPAQRL可以用来表示元结构。元结构相关性计算操作也可以在SPARQL上定义。
-
合成元路径。元结构也可以通过合成现有的元路径来构建。例如,从图2(b)中的两条元路径P1和P2,我们可以通过组合P1和P2中的公共节点A1、P1、P2、A2来形成元结构S。
上述解决方案假设用户对HIN模式和元结构有一定的了解。一旦定义了这些元结构,它们就可以存储在系统中,供非专家用户选择。最近,在[12]中已经开发了基于示例的算法,其中用户首先提供相关源和目标对象的一些示例对。该算法然后发现可能的元路径,最好地解释了示例对之间的关系。研究如何扩展此方法以支持元数据的自动发现是很有意思的结构。
3.1基于元结构的相关性
给定一个HIN G = (V,E)和一个元结构S,我们将源对象 和目标对象
和目标对象 的相关性函数定义如下:
的相关性函数定义如下:
![]()
其中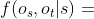 是在符合S的元结构的一些实例s上定义的相关性度量。 我们用s∈S来表示G上S的所有实例的集合。
是在符合S的元结构的一些实例s上定义的相关性度量。 我们用s∈S来表示G上S的所有实例的集合。
例如,给定图1中的HIN G和图2(b)中的元结构S,图3中显示了S的两个可能的实例。 让我们定义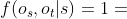 当且仅当
当且仅当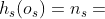 和
和 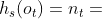 。然后,
。然后,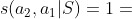 ,
,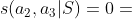 。
。
我们现在可以定义我们打算在本文中研究的相关性搜索问题。
定义4。相关性搜索问题。给定一个HIN G = (V,E),一个元结构 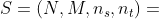 ,一个相关性度量f(·),以及一个源对象
,一个相关性度量f(·),以及一个源对象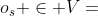 ,按照
,按照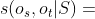 的降序返回一个目标对象的排序列表,这样对于列表中的任何一个对象,
的降序返回一个目标对象的排序列表,这样对于列表中的任何一个对象,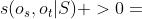 。
。
相关性搜索问题在许多应用中普遍存在,如信息检索和推荐。例如,一个作者可以使用图2(b)中的元结构来找出潜在的合作作者列表。在我们的实验中,我们还在实体解析、排序和聚类的背景下研究这个问题。我们注意到这个问题的一个有用的变体是返回topk目标对象(即那些相关性得分在k最高的对象),其中k由用户指定。
4.元结构的度量
在本节中,我们将展示如何定义基于元结构实例的相关性度量。具体来说,我们定义了基于结构的相关性度量、结构计数和结构约束子图扩展(SCSE)。然后,我们提出了SCSE的一个变种,有偏结构约束子图扩展,它是结构计数和SCSE的推广。最后我们详细分析了BSCSE的递归树,给出了BSCSE的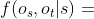 的明确定义。
的明确定义。
4.1结构计数
一个简单的相关性度量是计算图中以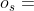 (
(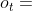 )作为源(目标)节点的元结构实例的数量:
)作为源(目标)节点的元结构实例的数量:
定义5。结构计数。给定一个HIN G = (V,E),一个元结构 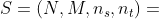 ,一个源对象
,一个源对象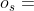 和一个目标对象
和一个目标对象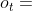 ,结构计数的值定义为s ∈ S的实例数,这样
,结构计数的值定义为s ∈ S的实例数,这样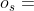 和
和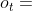 分别映射到
分别映射到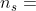 和
和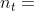 。回忆定义3中定义的映射函数hs(·)。形式上,对于StructCount的相关性测度f,如果存在用于s的映射函数
。回忆定义3中定义的映射函数hs(·)。形式上,对于StructCount的相关性测度f,如果存在用于s的映射函数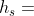 ,则
,则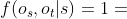 ,这样
,这样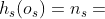 ,
,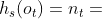 。
。
以图1中的HIN G和图2(b)中的元结构S为例。如果我们设置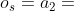 ,
,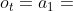 ,那么G上S的结构计数为1,即StructCount(a2,a1| S) = 1。原因是只有一个实例,即图3中的S1正确地将A2映射到a1和a1映射到A2。
,那么G上S的结构计数为1,即StructCount(a2,a1| S) = 1。原因是只有一个实例,即图3中的S1正确地将A2映射到a1和a1映射到A2。
我们可以直接使用StructCount来度量HINs上的相关性。但是,就像基于元路径的框架中的PathCount一样,StructCount的值是没有边界的。这使高度可见的对象产生偏差(即,具有较高度数的对象往往具有较大的结构计数值)。当我们喜欢流行的对象时,这可能是有用的,但是在一些我们喜欢高度相关的对象而不是流行的对象的应用程序中,例如共同作者推荐,结构计数是不合适的。
4.2 SCSE
事实上,结构计数是一个有偏见的措施,促使我们定义另一个相关性措施,命名为结构约束子图扩展(SCSE)。直观地说,SCSE模拟了源对象对象扩展到覆盖目标对象对象对象对象的实例的概率。由于SCSE值介于0和1之间,它消除了高度可见节点的偏差。
在定义SCSE之前,我们首先需要为元结构定义一个层的概念。
定义6。元结构层。给定一个元结构 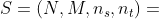 ,我们可以根据它们在S中的拓扑顺序,将它的节点划分为 w.r .t .。具体地说,我们用S[i] ⊆ N表示第i层的节点,用S[i : j] (1 ≤ i ≤ j)表示从第I层到第j层的节点。我们用
,我们可以根据它们在S中的拓扑顺序,将它的节点划分为 w.r .t .。具体地说,我们用S[i] ⊆ N表示第i层的节点,用S[i : j] (1 ≤ i ≤ j)表示从第I层到第j层的节点。我们用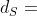 表示层数,因此
表示层数,因此![S[1:d_{S}] = N](https://yyzqsoft.com/uploads/202407/04/adb85b2b904a38bb.gif) 。注意S[ ·]是N中节点的划分,因此对于任何 i ≠ j,S[i] ∩ S[j] = ∅.
。注意S[ ·]是N中节点的划分,因此对于任何 i ≠ j,S[i] ∩ S[j] = ∅.
例如,图2(b)中的元结构S有dS= 5层。即1 ≤ i ≤ 5的S[i]分别为{A1}、{P1}、{V,T}、{P2}和{A2}。
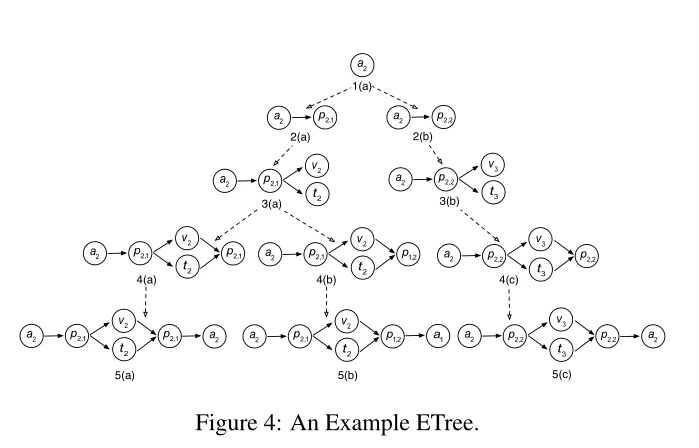
给定一个HIN G和一个元结构S,从一个源对象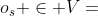 开始,我们可以在S层之后生成所有可能的实例s∈S。例如,给定一个HING(图1)和一个元结构S(图2(b)),从一个实例
开始,我们可以在S层之后生成所有可能的实例s∈S。例如,给定一个HING(图1)和一个元结构S(图2(b)),从一个实例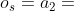 开始,我们可以通过递归扩展G的子图生成G上s∈S的所有实例,如图4所示。
开始,我们可以通过递归扩展G的子图生成G上s∈S的所有实例,如图4所示。
为了定义子图扩展的过程,我们用σ(g,i | S,G)表示从g∈S[1 : i]扩展到G的第(i + 1)层的实例。例如,如果G是图4中的图3(a),那么σ(g,3 | S,G)是包含图4(a)和4(b)的集合,因为它们是从g扩展而来的S[1 : 4]的实例。
基于这些符号,我们现在转向一个更公正的衡量标准,定义如下
定义7。结构约束子图扩展(SCSE)。给定HIN G = (V,e)、元结构s、源对象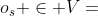 和目标对象
和目标对象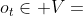 ,第i层子图g⊆G的SCSE递归地定义如下:
,第i层子图g⊆G的SCSE递归地定义如下:
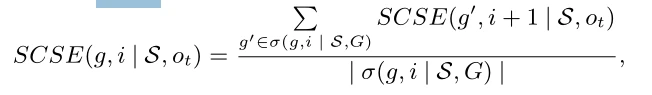
其中基本情况是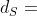 层的实例。SCSE(g,
层的实例。SCSE(g,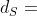 | S,
| S,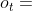 ) = 1当且仅当存在关于g的映射函数
) = 1当且仅当存在关于g的映射函数 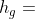 ,使得
,使得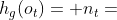 。我们对
。我们对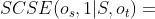 感兴趣。
感兴趣。
例如,给定图1中的HIN G,图2(b)中的元结构S,以及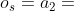 ,
,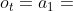 ,从
,从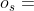 开始,我们在图4中展示了子图扩展的过程。在最后一层,即基本情况下,只有5(b)正确地将a1映射到A2(5(a)和5(c)没有a1)。在第一层,我们推导出我们感兴趣的
开始,我们在图4中展示了子图扩展的过程。在最后一层,即基本情况下,只有5(b)正确地将a1映射到A2(5(a)和5(c)没有a1)。在第一层,我们推导出我们感兴趣的 。
。
我们可以看到,SCSE对G(即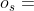 )的初始子图扩展到S覆盖
)的初始子图扩展到S覆盖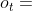 的实例的概率进行建模。显然,SCSE值介于0和1之间,因此它可以消除对高度可见对象的偏差。
的实例的概率进行建模。显然,SCSE值介于0和1之间,因此它可以消除对高度可见对象的偏差。
4.3 BSCSE:统一的衡量标准
根据上面的定义,我们观察到StructCount和SCSE都将搜索限制在能够严格匹配元结构的子图上。例如,结构计数测量这种子图的绝对数量,而SCSE应用从源对象到覆盖目标对象的实例的图扩展。每种措施都有其利弊。为了充分利用这两种度量,并将它们结合在一个统一的框架中,我们提出了SCSE的一个变体,称为有偏结构约束子图扩展(BSCSE),定义如下。
定义8。有偏结构约束子图扩展(BSCSE)。给定HIN G = (V,E)、元结构s、源对象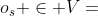 和目标对象
和目标对象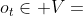 ,第i层子图 g⊆G的BSCSE递归地定义如下:
,第i层子图 g⊆G的BSCSE递归地定义如下:
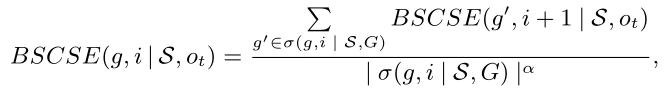
其中对于基本情况,即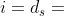 ,我们有BSCSE(g,
,我们有BSCSE(g,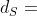 | S,
| S,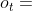 ) = 1当且仅当存在关于g的映射函数
) = 1当且仅当存在关于g的映射函数 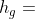 ,使得
,使得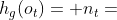 。我们对
。我们对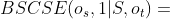 感兴趣。
感兴趣。
注意,α ∈ [0,1]是一个偏置因子,用来平衡结构计数和SCSE之间的权重:(1)较小的α更关心匹配元结构的子图的数量(如果α = 0,BSCSE降为structure count);(2)较大的α更侧重于随机展开可以覆盖目标物体的可能性(如果α = 1,BSCSE降为SCSE)。另一方面,由于我们将结构计数和SCSE结合到一个统一的BSCSE框架中,我们可以只关注BSCSE的计算。
4.4 ETree
在这一小节中,我们分析了BSCSE的扩展过程,并给出了BSCSE的相关性度量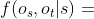 的明确表达式。
的明确表达式。
正如我们在定义8中看到的,BSCSE的计算模拟了子图展开的过程。如果我们跟踪从原始源对象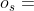 到实例s∈S的扩展路径,我们可以得到一个递归的子图扩展树。我们定义这个递归树 Etree,如下所示:
到实例s∈S的扩展路径,我们可以得到一个递归的子图扩展树。我们定义这个递归树 Etree,如下所示:
定义9。ETree。给定一个HIN G,一个元结构S和一个源对象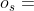 ,结构ETree表示为ETree = (T,L,w),其中
,结构ETree表示为ETree = (T,L,w),其中
- T:树节点集,其中每个节点都是G的子图;
- L:边集;
- w:将树节点v∈T映射到其权重w(v)的函数w(·)。权重是基于v的父u定义的,即(u,v) ∈ L,它考虑 (1) u的权重w(u),和 (2)u的#子,即|{v'|(u,v') ∈ T}|。具体来说,我们有
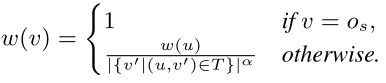
例如,给定图1中的G和图2(b)中的S,从a2开始的ETree如图4所示。我们可以看到,根是a2,每条边都把一个子图链接到它的一层扩展w.r.t. S .中的一个,例如,a2既可以扩展到{a2,p2,1}也可以扩展到{a2,p2,2} w.r.t. S,它们的权重都是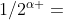 。叶节点(深度为dS)包含从a2开始的所有S实例。
。叶节点(深度为dS)包含从a2开始的所有S实例。
接下来,我们分析了ETree的两个属性,与其高度(属性1)和节点(属性2)相关,这有助于表达我们感兴趣的值,即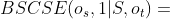 (定理1)。
(定理1)。
属性1。ETree的高度最多为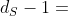 。
。
证明。ETree的根是s的第一层的源对象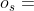 ,假设
,假设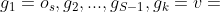 是从
是从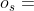 离开节点v的路径,每一步都意味着子图的一层扩展。我们从
离开节点v的路径,每一步都意味着子图的一层扩展。我们从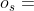 到v最多有
到v最多有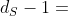 层扩展。因此,ETree的高度最多为
层扩展。因此,ETree的高度最多为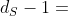 。
。
属性2。深度d处ETree的每个节点都是S[1 : d+1]的一个实例,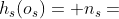 的S[1 : d+1]的每个实例都必须是深度d处ETree的一个节点。
的S[1 : d+1]的每个实例都必须是深度d处ETree的一个节点。
归纳证明。当d = 0时,根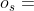 仅是S[1:1]的一个实例,
仅是S[1:1]的一个实例,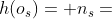 。假设属性2对于d = k成立,假设u是深度k + 1处ETree的节点,其父节点为v,那么u ∈ σ(v,k + 1 | S,G)为(v,u) ∈ L,所以u一定是S[1 : k+2]的一个实例。另一方面,∀s ∈ S[1 : k+2],s' = s- { v∈s | hs(v)∈s[k+2]}必须是S[k + 1]的实例,这意味着s是s'的一层扩展。所以s是ETree在深度k+1的节点。
。假设属性2对于d = k成立,假设u是深度k + 1处ETree的节点,其父节点为v,那么u ∈ σ(v,k + 1 | S,G)为(v,u) ∈ L,所以u一定是S[1 : k+2]的一个实例。另一方面,∀s ∈ S[1 : k+2],s' = s- { v∈s | hs(v)∈s[k+2]}必须是S[k + 1]的实例,这意味着s是s'的一层扩展。所以s是ETree在深度k+1的节点。
定理1。给定一个元结构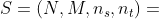 ,源对象
,源对象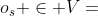 和目标对象
和目标对象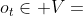 ,
,

证明。假设s是S的一个实例,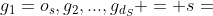 是ETree从
是ETree从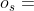 到s的路径,根据BSCSE的递归定义,
到s的路径,根据BSCSE的递归定义,
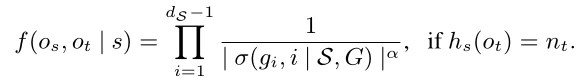
根据属性1和2,S必须是深度为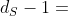 的叶节点,P必须是ETree从根
的叶节点,P必须是ETree从根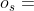 到s的路径,根据w的定义,
到s的路径,根据w的定义,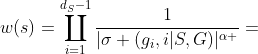 ,那么我们最终可以推导出
,那么我们最终可以推导出
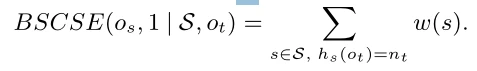
基于定理1的证明,我们知道BSCSE的相关测度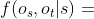 为:
为:
以图1中的HIN为例,我们用表1中的三个度量显示了两对作者的相关值。我们可以看到,我们的三个元结构相关性度量可以更好地处理复杂关系,即(a2,a1)的相关性得分大于(a2,a3)。这是因为元结构可以利用不同元路径中公共节点的信息。
5.计算BSCSE
我们知道,BSCSE是StructCount和SCSE的推广。因此,在本节中,我们研究如何基于给定的源对象 ,利用BSCSE(也适用于StructCount和SCSE)有效地执行相关性搜索。我们首先提出了一种基于ETree的遍历算法(第5.1节),然后通过提出两种优化来进一步提高其效率(第5.2节)。
,利用BSCSE(也适用于StructCount和SCSE)有效地执行相关性搜索。我们首先提出了一种基于ETree的遍历算法(第5.1节),然后通过提出两种优化来进一步提高其效率(第5.2节)。
5.1遍历算法
为了计算BSCSE(os,1|S,G),最初的想法是访问ETree的所有叶节点,并累加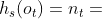 的所有s∈S的权重。在此基础上,我们开发了一个递归算法,称为遍历(算法1)来计算BSCSE。它首先检查基本案例是否被捕获,即g是否已经是S的实例。在这种情况下,返回具有权重w的实例g(步骤1-2)。算法的其余部分由两个阶段组成。第一阶段(步骤3-11)计算集合σ(g,layer| S,G),第二阶段(步骤12-17)递归调用每个g'∈ σ(g,layer| S,G)的算法并累加结果。
的所有s∈S的权重。在此基础上,我们开发了一个递归算法,称为遍历(算法1)来计算BSCSE。它首先检查基本案例是否被捕获,即g是否已经是S的实例。在这种情况下,返回具有权重w的实例g(步骤1-2)。算法的其余部分由两个阶段组成。第一阶段(步骤3-11)计算集合σ(g,layer| S,G),第二阶段(步骤12-17)递归调用每个g'∈ σ(g,layer| S,G)的算法并累加结果。
在第一阶段,对于S的第(i + 1)层的每个节点n,我们考虑所有节点n',使得(n',n) ∈ M,检查其实例对象g[n']并计算可能的实例对象w.r.t .节点n(步骤6-8)。然后,我们计算满足所有依赖约束的实例对象w.r.t. n(步骤9)。最后,我们计算层(i+1)上每个节点的可能实例的笛卡尔积,并导出可能展开的集合σ(步骤11)。
在第二阶段,我们首先根据定义9记录层(i + 1)的权重w'(步骤12)。然后,对于每个可能的扩展,我们将子图g扩展到g'(步骤15),并递归调用扩展的子图g'上的算法,以获得S的所有实例及其相应的权重(步骤16)。
例如,假设我们基于图2(b)中的元结构遍历图4中的ETree。我们将图层设置为3,将g设置为3(b)中的图形。第一阶段,第四层只有一个元节点n,即n = P2,n依赖于两个节点,即V和t,然后我们可以看到g[V] = v3,它有两个邻居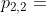 和
和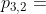 ;g[T] = t3,它有两个邻居
;g[T] = t3,它有两个邻居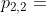 和
和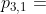 。我们得到C = {{
。我们得到C = {{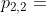 ,
,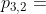 },{
},{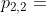 ,
,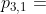 }},
}},![Ins[P_{2}]=\bigcap C=\left \{ {p_{2,2}} \right \}](https://yyzqsoft.com/uploads/202407/04/a9b82181facf110a.gif) ,这意味着P2只有一个可能的实例对象。在第二阶段,我们有w‘’= w,因为只有一个可能的扩展。然后我们计算扩展子图
,这意味着P2只有一个可能的实例对象。在第二阶段,我们有w‘’= w,因为只有一个可能的扩展。然后我们计算扩展子图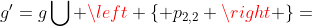 ,递归调用遍历算法(G,S,g',w',4)。
,递归调用遍历算法(G,S,g',w',4)。
5.2优化
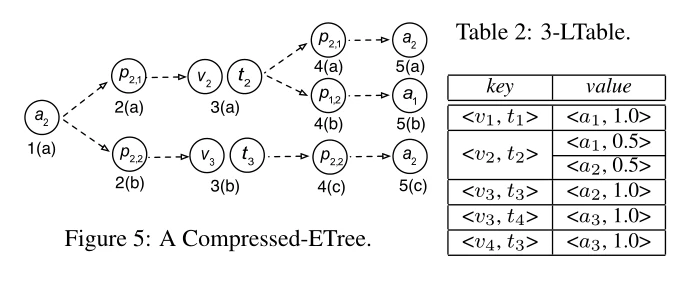
为了提高效率,我们对遍历算法进行了两次优化。首先,我们设计了一个ETree的压缩表示来减少冗余。然后,我们提出了一个索引结构来进一步加速在线查询的过程。

Compressed-ETree
根据属性2,在深度为d的ETree的内部节点v上,我们需要维护一个S的实例[1:d + 1]。然而,要进一步扩展v,我们不一定需要整个实例的信息。相反,我们只需要维护一个v的子集,在这个子集上d之后的S的层有依赖关系。例如,在图2(a)(图4)中,我们不需要维护整个图;相反,{ }足以表示它,因为元结构的其余部分仅依赖于节点
}足以表示它,因为元结构的其余部分仅依赖于节点 。
。
基于这个想法,我们开发了一个压缩结构,称为压缩-ETree,如图5所示。我们可以看到,与ETree相比,它更加简洁(图4)。因此,通过遍历压缩树而不是树,我们可以减少计算成本和每个树节点所需的空间。
为了导出压缩的ETree,我们必须直观地预先计算和维护元结构每一层的必要节点,我们称之为依赖集。我们使用一个映射结构来存储需要在每一层维护的节点。细节如算法2所示。特别地,对于S中的每个节点n',我们首先得到该节点能够到达的最大层,即依赖于n'(步骤3)。然后我们将n'添加到相应的D层(步骤4-5)。在所有的节点都被添加到D之后,我们可以在D[i]中的i层得到我们需要维护的节点集。以图2(b)中的S为例;i = 1到5的依赖集D[i]分别为{A1}、{P1}、{V,T}、{P2}和{A2}。
通过考虑依赖集D[*],我们可以通过遍历Compressed-ETree而不是ETree来提高性能。该算法与算法1略有不同。在步骤16,我们可以只维护g'的一个子集,它在依赖集D[layer+1]中,而不是在整个g'子图上递归调用它。

i-LTable
压缩的ETree可以减少ETree每个节点的计算量,但它仍然有相同数量的树节点。尤其是如果我们有一批查询要回答,计算中会有很多冗余。例如,当计算图1中两个源对象a2和a1的BSCSE时,我们必须分别遍历a2和a1的两个压缩对象。当遍历a2的一个时(图5),我们访问一个以3(a)为根的子树;同时,我们将访问同一个子树,同时遍历a1的另一个压缩树。这是因为元结构S[4,5]的最后两层只依赖于S[3](而不是S[1,3])。
基于这一思想,我们提出了一种新的数据结构i-LTable,它预先为压缩树的一个子树存储所有的叶子节点。一旦我们遍历到第i层,我们就可以直接从i-LTable获取叶节点的信息,这样就节省了从第(i+1)层到最后一层的搜索时间。
给定一个S,i-LTable w.r.t .第一层是一个数据结构,它将第一层的Compressed-ETree的每个节点实例v映射到最后一层的所有节点实例(以v为祖先)。具体来说,i-LTable的键是D[i]中存储的节点的实例,值是所有可能的目标对象的权重分布。给定图2(b)中的S,考虑图5中的压缩表,相应的3-表如表2所示。例如,当D[3] = {V,T},目标节点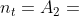 时,3-LTable的键是地点和主题对,值是作者权重的分布。
时,3-LTable的键是地点和主题对,值是作者权重的分布。
接下来,我们研究如何为给定的元结构离线构建一个I-LTable。首先,我们处理I的选择,即i-LTable应该构建在哪个层上,然后我们处理如何离线构建索引和在线进行查询。
选择一个合适的i .如果我们已经在第I层构建了i-LTable,那么我们只需要在压缩的ETree中搜索最上面的i层。直觉上,I的选择是时间和空间的权衡。对于较小的I,需要访问的节点数量较少,因此处理效率较高。然而,可到达的目标对象的数量很大,导致更大的空间需求。我们接下来列出了三种关于如何选择I的启发式方法:(1) MinKey:用最少的可能键值选择i;(2)一半:选择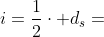 (3) Min:选择一个空间预算受限的最小I。
(3) Min:选择一个空间预算受限的最小I。
脱机构建索引。选择一个i后,我们可以开始构建I-LTable,细节如算法3所示。在检索到D[i]中的节点后,我们可以通过遍历压缩树的子树来为每个可能的键构建i-LTable。
在线查询处理。一旦我们建立了i-LTable,我们就可以加快在线查询的过程。该算法类似于算法1,只是它只需要遍历顶部I层的压缩树。然后可以直接从i-LTable中检索结果,而不是递归搜索子树。

6.实验
我们现在讨论实验结果。第6.1节描述了实验设置。然后我们检查不同相关性度量的有效性(第6.2节)和效率(第6.3节)。
6.1设置
我们检查两个HIN数据集,即Y AGO和DBLP。
Y AGO[15]是从维基百科、WordNet、GeoNames衍生出来的大规模知识图。我们使用它的“核心事实”,即Y AGOCore [12],它由125种类型的400万个事实(边)组成,由210万个对象组成。这些实体有365,000种类型。
DBLP是一个书目网络。它包含四种类型的对象,即论文、作者、地点和主题。我们使用DBLP的一个子集,即DBLP-4-Area [12],包含5,237篇论文、5,915名作者、18个地点和4,479个来自4个领域的主题:数据库、数据挖掘、机器学习和信息检索。这些对象由51,377条边连接。
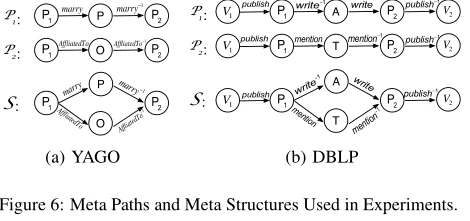
我们将我们的相关性度量(即结构计数、SCSE和BSCSE)与三个有代表性的元路径度量(即路径计数[18]、PCRW [7]和路径模拟[18])进行比较。这些措施采用了图6所示的元路径和结构。我们在一台8GB内存的苹果OS X机上用C++实现了实验。
6.2有效性
我们比较了三种应用中相关性度量的质量:实体解析(第6.2.1节)、排序(第6.2.2节)和聚类(第6.2.3节)。然后我们在第6.2.4节和第6.2.5节中研究了元结构的性质。
6.2.1实体解析
我们首先执行一个实体解析(ER)任务,以在YAGO查找引用同一实体的对象对。例如,巴拉克·奥巴马和巴拉克·奥巴马的总统这两个对象指的是同一个人。识别这样的对有助于通过消除条目的重复来“清理”一个HIN。
我们手动标记一小部分数据。我们寻找与一个对象都有婚姻关系的(人类)对象对。我们总共得到3020对这样的人,包含4518个不同的人。我们将这些视为我们的测试数据,并手动标记它们的基本事实。我们得到了44个阳性样本(即每个对象对指的是同一个人),而剩下的2976个样本是阴性的。
我们使用图6(a)中的元结构S和两个元路径(P1,P2)来计算相关性。对于每个人(4518个中的一个),我们将其设置为S、P1、P2的源对象,并使用它们来查找目标对象,这些目标对象可以是重复的。然后,我们得到所有(目标)人,使得相对于源对象的相关性值大于零。相关性越大,对象对越有可能指同一个人。对于每个相关性度量,我们改变所有返回对的相关性值的阈值,并绘制精度-召回曲线。然后我们计算曲线下的面积,即AUC。
不同指标的AUC值如表3所示。观察到元结构的度量比元路径的度量更有效。这是因为S比单个元路径(即(P1or P2))更有表现力。在这里,S把结果限制在那些嫁给同一个人,隶属于同一组织的人,不能单独用P1或p2来表示。
然后我们研究两个元路径的线性组合的有效性。相关性计算为s =β·s1+(1-β)·s2,其中s1和s2分别是由P1和P2导出的相关性。如图7(a)所示,两个元路径的线性组合比单独使用P1或 P2要好。然而,由于它没有考虑元路径中的公共节点(即节点P1和P2),基于最优β,它的AUC值仅为0.2920,并且仍然比SCSE差(即0.5640)(表3)。
我们还研究了参数α如何影响BSCSE的有效性。如图7(b)所示,对于大范围的α值,其AUC是稳定的。当α = 1时,BSCSE的结果最好。这与我们的预期是一致的,因为实体解析更倾向于高度相关的对象,而不是流行的对象。
接下来,我们在表4中显示了PCRW和SCSE的前10个相关对(对于PCRW,我们使用具有最佳β的线性组合,获得最佳AUC值)。粗体的对是阴性样本。我们看到PCRW在前十对中有三个阴性样本。例如,莎莉·海弗伦和格雷斯·穆加贝出现在结果中的原因是他们已经嫁给了同一个人,并且由于元路径P1的权重支配着另一个(P2),所以这对夫妇有很高的分数,即使这两个人不满足P2。这解释了为什么基于元路径的度量比基于元结构的度量具有更低的AUC值。
6.2.2排名质量
在我们的第二个有效性实验中,我们执行了如下相关性排名任务。我们首先使用三个级别来标记DBLP每对场馆的相关性:0表示“不相关”,1表示“有点相关”,2表示“非常相关”。我们在贴标签时会考虑场馆的水平和范围。例如,西格蒙德和VLDB的相关性得分为2,因为它们高度相关。我们使用元结构S和两条元路径P1,P2如图6(b)所示。然后,我们使用归一化贴现累计增益(nDCG)来评估返回的排名列表的质量,nDCG是排名质量中常用的度量,越大越好。
结果如表3所示。我们可以观察到,在所有三个基于元路径的测量上,第一元路径P1= VPAPV比第二元路径P2=VPTPV产生更好的结果。然而,总体而言,基于元结构的度量比基于元路径的度量表现更好。

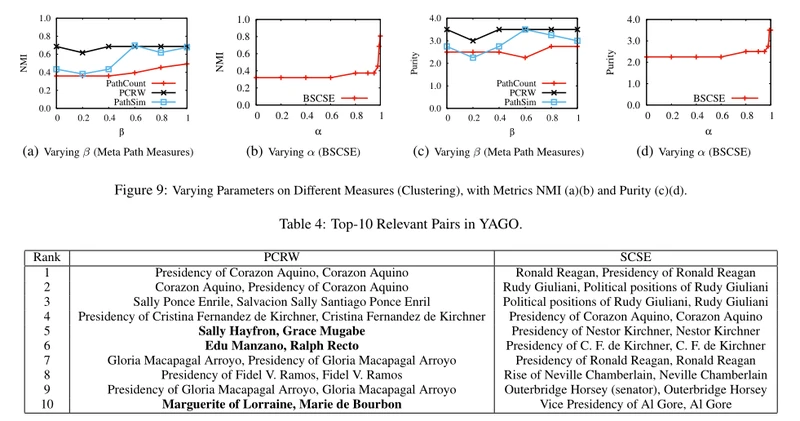
我们还比较了两个元路径的线性组合。我们改变权重β ∈ [0,1]来权衡P2的P1,并记录排名结果的nDCG值。结果如图8(a)所示。在基于元路径的度量中,PCRW的表现优于路径计数和路径模拟。我们可以看到,质量随着β的增加而变好。这意味着两个元路径的线性组合并不能得到比p1本身更好的结果。
我们进一步研究了参数α对排序质量的影响。我们变化α ∈ [0,1],观察返回排名列表的质量。如图8(b)所示,当α = 0.8时,BSCSE达到最佳nDVG值。在表3中,我们看到最佳α (0.8)的BSCSE优于元路径的线性组合。
6.2.3聚类质量
类似于上面的实验,在图6(b)中给定相同的元结构和元路径,为了进一步评估场馆之间的相关性值的质量,我们执行了在DBLP对场馆进行聚类的任务。具体来说,Weapplyk-means推导出的相关矩阵具有不同的度量。我们使用两个评估指标,归一化互信息(NMI)和纯度(两者都越大越好)。结果如表3所示。我们可以看到,SCSE在所有指标中表现最好。
我们进一步比较了这两种元路径的线性组合。加权β ∈ [0,1]来权衡offP1,并记录聚类精度。结果如图9(a)(c)所示。可以看出,PCRW的性能优于PathCount和PathSim,其性能随β变化不大。同样,从表3中,我们观察到两个元路径的线性组合不能获得比P1本身更好的结果。不管我们给多少权重,基于元路径的度量的聚类精度并不比SCSE好。
我们还研究了α在聚类任务中如何影响BSCSE。结果如图9(b)(d)所示。我们可以看到,α越大,聚类精度越好。当α = 1时,我们的聚类精度最好。
我们观察到,在不同的任务(如排序和聚类)中,BSCSE在不同的α值下获得最佳性能。这就引出了如何设置α的问题。为了简单起见,我们可以设置α = 1,因为SCSE(即α = 1)在我们执行的所有任务中具有相当好的性能。另一方面,α可以设置为用户输入,或者可以在实验中用训练数据进行调整。
6.2.4元结构的语义
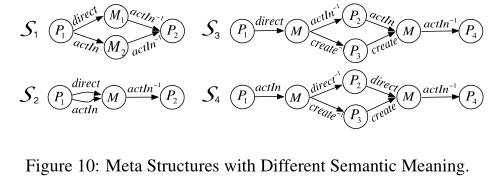
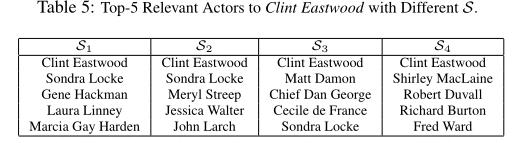
不同的元结构意味着不同的含义。我们在Y AGO上进行了一个案例研究,表明使用不同的元结构,我们可以找到完全不同的top-k结果,具有不同的关系。具体来说,我们用图10中的四种不同的元结构来查询YAGO中的一位著名演员兼导演克林特·伊斯特伍德,以找到与他相关的前5名演员。
我们根据表5中前5名的结果进行了分析:(1)桑德拉·洛克在S1和S2的结果中排名很高,但在S3和S4的结果中相关性较低。这是因为S1和S2更短,他们倾向于找出直接与伊斯特伍德合作的演员,例如桑德拉·洛克。另一方面,S3和S4更长,所以他们倾向于寻找像马特·达蒙和雪莉·麦克莲恩这样的著名演员。(2)马特·达蒙在S3中排名很高,因为他与参加过伊斯特伍德执导的电影的演员和创作者进行了大量合作。(3)同样,雪莉·麦克莲恩在S4中名列前茅,因为他与伊斯特伍德参演过的电影的导演和创作者进行了大量合作。
我们可以得出结论,不同的元结构,前5名的结果是不同的。虽然S1和S2的长度相同,但S1和S2与S2不同,只考虑伊斯特伍德同时担任导演和演员的电影,而S1的约束更宽松。虽然s3a和s4a都有dS= 5,但是s3a只考虑他导演的那些电影,s4a只考虑他演的那些电影。我们想表明,由于元结构比元路径更复杂,用户可以使用具有细微差异的元结构来表达不同的相关性。
6.2.5元结构大小的影响
我们研究不同大小的元结构的影响。特别是,我们研究以下情况是否成立:更大的尺寸(即dS)是否导致元结构的更好质量?
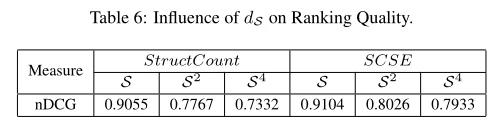
为了测试不同大小的有效性,我们使用了图6(b)中的元结构的连接,即S,S2和S4。直觉上,有了S,两个场地如果分享同一个作者,同一个话题,就是相关的。然而,对于S2和S4,相关性变得更加微妙,因为元结构涉及远程对象。当大小趋于无穷大(∞)时,top-k结果趋于全局结果。我们还比较了类似于第6.2.2节的排名质量(即nDCG)。如表6所示,元结构越大,排序结果越差。
6.3效率
我们进行了两个实验来研究第5节中提出的算法和两种优化技术的效率。为了便于展示,我们表示如下:
- 遍历+:带有压缩-ETree优化的遍历算法(没有索引);
- 遍历++:在其上建立索引的遍历+。
在这一节中,我们首先比较遍历的执行时间,遍历+和元路径度量。然后,我们研究了遍历++中不同索引(即I)的影响。
6.3.1与元路径度量的比较
我们从比较BSCSE的运行时和元路径度量的运行时开始。在DBLP,我们使用图6(b)中的元结构和元路径运行了18个查询,将源对象设置为不同的地点。此外,我们使用图2(b)中的元结构和元路径,从随机选择的作者开始运行了1000个查询。在Y AGO上,我们基于图6(a)中的元结构和元路径对1000多名随机选择的人进行了查询。我们记录了每个查询包的平均执行时间,如表7所示。我们可以看到基于元路径的度量对于不同的元路径有不同的运行时性能。例如,场馆的P2query比所有三个基于元路径的度量的P1query多20倍。请注意,就效率而言,BSCSE并不比基于路径的元度量差。此外,压缩-ETree优化可以稍微提高效率,因为它可以减少表示中的冗余。
为了进一步解释这个现象,我们通过不同的元结构和元路径来分析实例的数量。如表8所示,实例的数量与执行时间成正比。我们还可以看到,元结构的实例数量很少,因为与元路径相比,它们更具限制性。
6 . 3 . 2 i-LTable的影响
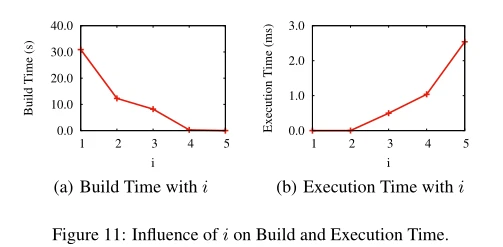
我们在图11(a)中显示了不同I值下离线构建I-LTable的时间。我们可以看到,随着I的增加,构建I-LTA table的时间减少。特别是,如果我们选择i =1 2dS= 3,我们需要10s来构建i-LTable。
图11(b)显示了针对不同I值使用I-LTA table进行在线查询的时间(i = 5表示我们不使用I-LTA table作为dS= 5)。我们可以看到i-LTable大大降低了在线查询的成本。特别是,如果我们选择i = 1 2dS= 3,遍历++算法只需要0.5毫秒,而遍历+需要2.45毫秒。

7.结论和未来工作
在本文中,我们引入了元结构的概念,它是元路径的一个强有力的扩展。基于元结构,我们在异构信息网络上引入了一个相关性框架,它可以表达两个对象的复杂相关性。特别地,我们在这个框架下定义了两个相关性度量,即结构计数和SCSE。SCSE模拟了子中缝扩展的过程,并设计了一个高度可视的对象。此外,我们定义了一个名为BSCSE的统一度量,它将结构计数和SCSE结合到同一个框架中。为了有效地计算BSCSE,我们提出了一个递归算法和两个优化(Compressed-ETree和i-LTable)来提高效率。在真实数据集上的实验证明了该方法的有效性和高效性。
在未来,我们将研究从知识库中自动学习元结构的方法。我们还将研究元结构在不同应用中的使用,如引文推荐和论文审稿人分配。
