目录
差错控制编码的基本概念:
差错控制编码的主要类型和方式:
差错控制编码的主要类型:
差错控制方式:
简单的差错控制方法:
奇偶校验码:
重复码:
信道编码的基本概念和定理*:
信道编码的基本概念:
最大后验译码准则:
定义编码速率(纠错编码的信息率)定义为:
归一化信道容量:
信道编码定理:
信道编码定理的意义:
差错控制编码的基本概念:
通过对数据进行某种编码处理,使得接收端可以判断接收到的数据,是否出现错误,甚至可以纠正一定范围内错误。差错控制编码是将有误码的物理信道改造成无差错的逻辑信道的一种方法。
所谓差错控制编码,通常是通过代数的方法,加入与待传输的数据有一定关联关系的监督位来实现的。在接收端可根据特定的关联关系是否受到破环来判别是否出现错误,并可在一定程度上根据出错的情况纠正错误。在纠错编码中加入的监督位本身并不携带信息,因此有时也将监督位成为冗余位。
若每一组 k 位信息位,编码后生成 n 位长度的码字,则定义编码效率:
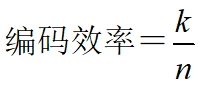
冗余度:
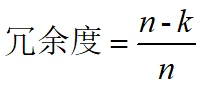
差错控制编码的主要类型和方式:
差错控制编码的主要类型:
(1)线性码与非线性码
线性码:监督码元与信息码元间的关系是一种线性关系;
非线性码:监督码元与信息码元间的关系则是一种非线性的关系。
(2)分组码与卷积码
分组码:监督码元与信息码元间以码组为单位建立关系;
卷积码:监督码元不仅与本组的信息码元有关,还与前面若干个码组的信息码元有关。
(3)系统码与非系统码
系统码:编码后信息码元部分的排列结构保持不变;
非系统码: 编码后码组中信息码元部分的排列结构发生了变化,一般不能看出原来信息码元的图样结构。
通信系统通常可分为单工、半双工、和全双工三种工作方式。
单工:单向、没有回传通道的系统称之;
半双工:双向,但发送和接收必须分时进行的系统称之;
全双工:双向,发送和接收可同时进行的系统称之。
差错控制方式:
(1)检错重发:通过差错控制编码,使得接收端具有检错能力,接收端如果发现传输出错,通过反向信道请求重发。
检错重发方式,要求系统具有反向传输通道;
检错重发方式通常具有较高的编码效率。
(2)前向纠错:采用具有检错和纠错的编码算法,接收端不仅能够检测出错误,而且定位出码字中错误的位置并加以纠正。
前向纠错的方法适用于包括单工通信系统的应用场合。
在一些对实时性要求较高的通信场合,必须采用前向纠错的方法。
前向纠错需要定位错误的位置和出现何种错误(对二进制以外的纠错编码),通常编译码的方法比较复杂,效率较低、
(3)混合差错控制:结合检错重发和前向纠错方式优点的差错控制方法;
对于出现较少错误时,由前向纠错方式加以纠正;当经纠错后仍有错误时,则启动检错重发机制。
混合差错是一种兼顾效率和复杂性的方法。
简单的差错控制方法:
奇偶校验码:
奇偶校验码是一种通过增加1位监督位,从而使得码组具有检测1位误码的差错控制方法。
(1)偶校验:

(2)奇校验:

所有可能的信息码组经过差错控制编码后,得到的输出码组(也称为码字)构成了一个称为许用码字的集合:许用码字集
示例:偶校验码字中所有含偶数个“1”的码字为许用码字;所有含奇数个“1”的码字为禁用码字。奇校验码字中所有含奇数个“1”的码字为许用码字;所有含偶数个“1”的码字为禁用码字。如果传输过出错使得原来的许用码字变为另外一个许用码字,则这种错误不能被发现。


重复码:
在上例中可见,“000”和“111”是3位码元均相同,是一种3位的重复码,可发现任意的2位错误和纠正1位错误。3位的重复编码可推广到一般的情形,若 n 位的重复码用于表示1比特信息。如
![]()
则可发现任意的n-1位误码;采用择多逻辑进行判决,可纠正任意的少于n/2位的误码。重复码编译码简单,但效率较低。
信道编码的基本概念和定理*:
信道编码的基本概念:
编码信道的基本模型:




最大后验译码准则:

误码的概率:
![]()
正确译码的概率:
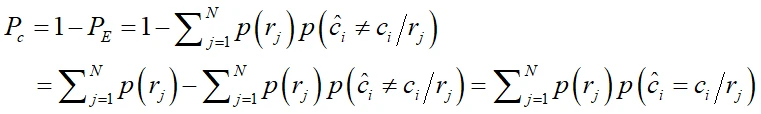
若规定译码规则
![]()
则可使得差错概率最小,最佳译码方法。
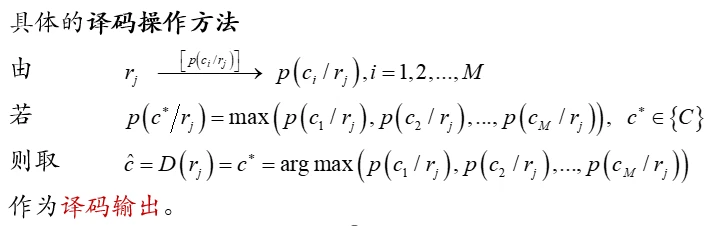




定义编码速率(纠错编码的信息率)定义为:
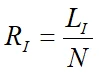
其中L为信息位长度,N为编码输出码字长度。
归一化信道容量:
已知离散信道的容量:
![]()
由信息论的基本知识,有:
![]()
定义归一化信道容量为:
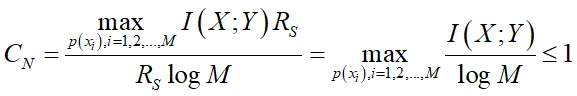
信道编码定理:
给定归一化信道容量Cn,若Ri<Cn,则Ri是可达的。
信道编码定理给出了编码速率Ri可达的基本条件
在信道编码定理的证明过程中,可得:
![]()
信道编码定理的意义:

信道可达性的定义包含了可通过增大码字的长度来改善信道编码误码性能的思想。
(1)纠正了传统的观点:信道编码的可靠性和有效性是一对不可调和的矛盾。为信道编码理论与技术的发展指明了方向。
(2)信道编码定理并没有告诉我们如何具体应如何编码,才能保证译码能够满足![]() 的条件。
的条件。
