1 亲和图的定义
为研究因数和函数F(n)(正整数n除n以外的正因数之和)的性质以及完全数、相亲数对、多元亲和数链等问题,定义一个无限有向图——亲和图。
亲和图的顶点集与非负整数集一一对应,(下文中将用某非负整数指代它所对应的顶点),对顶点n,若F(n)=m,则从n到m连一条有向边(n指向m),注意1指向0,0指向自己。
由以上定义得知:
(1)亲和图的所有性质为正整数集固有,整个图随正整数集和因数定义的建立而确定。
(2)亲和图中每个顶点出度都是1;入度不确定。
(3)完全数6,28等引出的边指向自己。
(4)相亲数对(220,284)等在图中呈现为一个两元环(220指向284;284指向220)。
我们希望得到图的其他性质,但无限图是不可能完全画出的。我们采取以下两个手段:一方面,我们希望知道对给定的一个点,哪些点指向这个点;另一方面,由于点给定时,它引出的路线也唯一确定,我们希望追踪这条路线通向哪里。
2 入度求解
0的入度为2,0和1指向它。
1的入度为无穷大。因为一个数直接指向1当且仅当它为素数,而素数有无穷多个。
对于0、1以外的数,我们说明,尽管图是无限的,每个顶点的入度只有有限多。
命题:
若F(n)=m,则n≤(m>1)
证明:
显然n是合数。当n不是平方数,取它除1以外最小的因数i,则n/i(不等于i)也是n的因数。此时有:
亦即
当n是平方数,它至少含因数,故有:
等号当且仅当是除1以外n的唯一因数时取得。
证毕。
根据这一命题,我们很容易写出求解入度的程序。
程序1:
功能:求m到n之间每个数的入度和指向它的所有顶点,结果保存于D:/1.txt。
使用:输入m n;
作者:Nithouson
代码:(C++)
#include <stdio.h>
#include <stdlib.h>
int SumofDivisors(int n)
{
int i,s=1;
for(i=2;i*i<n;i++)
{
if(n%i==0) s+=i+n/i;
}
if(i*i==n)
return s+i;
else
return s;
}
int main()
{
FILE*pad;
pad=fopen("D://1.txt","w");
int m,n,con,i;
scanf("%d %d",&m,&n);
int*s=(int*)malloc((n*n)*sizeof(int));
for(i=2;i<=n*n;i++)
s[i]=SumofDivisors(i);//空间换时间,预存所有因数和。
for(int j=m;j<=n;j++)
{
fprintf(pad,"%d ",j);
con=0;
for(i=2;i<=n*n;i++)
{
if(s[i]==j)
{
con++;
fprintf(pad,"%d ",i);
}
}
fprintf(pad,"(%d)\n",con);
}
free(s);
return 0;
}
我用此程序计算了1-1000的所有顶点入度,得出以下信息:
(1)有些非0数入度为0,如2、5、52、88、96等。事实上,1到1000中共有89个数入度为0,而且它们中只有5是奇数。
(2)100以内的入度最大值为9,在91和97取得;1000以内的最大值为56,在841取得。
(3)奇数入度通常比附近的偶数入度多。事实上,2-1000中奇数的平均入度为17.060,而偶数的平均只有1.409,差异非常明显。(10000以内偶数入度的最大值仅为5)
3 顶点集的盈亏
对一个顶点集,若总入度减总出度为正,称为盈余;否则称为亏损。
经计算,2-100盈余162;2-1000盈余8234。这或许意味着F(n)有整体减小的趋势。
4 路径追踪
从一个顶点出发,不断沿引出的边前进,其实质是F(n)无限次迭代的过程。我们设想以下结果。
(1)路线最终到达1,之后停在0。
(2)路线进入一个闭环中(可能为完全数、相亲数对或多元亲和数链),之后一直在闭环中循环。
(形式上0也可理解为一个闭环,但(1)(2)的成因有很大不同,故分成两种情况)
是否只有以上这两种结局呢?理想上希望如此,但这尚需证明。而且,程序必须满足有限步终止原则,并且不能超出整数变量表达范围。所以追加两种情形:
(3)某一步的值超出int的表达范围;
(4)有限步后(这里定为10000步)尚未达成(1)(2)(3)中任何一条。
条件编译程序如下,它可选择输出希望获取的四种情况之一。
程序2:
功能:求m到n之间每个数的前进路线和路线长度,结果保存于D:/1.txt。
使用:输入m n;
作者:Nithouson
代码:(C++)
#include <stdio.h>
#include <stdlib.h>
#define ONE 1 //到1终止
#define LOOP 2 //进入闭环
#define BEYONDLIM 3 //超过2147483647
#define OVERLONG 4 //运行超过10000次
int SumofDivisors(int n)
(同程序1)
int main()
{
FILE*pad;
pad=fopen("D://1.txt","w");
int m,n;
const int MAX=10000; //迭代次数上限
scanf("%d %d",&m,&n);
int s[MAX];
for(int i=m;i<=n;i++)
{
int j,br=0,p;
s[0]=i;
for(j=1;j<MAX;j++)
{
s[j]=SumofDivisors(s[j-1]);
if(s[j]<0) //超出2147483647后int会读成负数
{
#ifdef BEYONDLIM
for(p=0;p<=j-1;p++)
{
fprintf(pad,"%d->",s[p]);
}
fprintf(pad,"Beyond Limit\n");
#endif // BEYONDLIM
break;
}
if(s[j]==1)
{
#ifdef ONE
for(p=0;p<=j-1;p++)
{
fprintf(pad,"%d->",s[p]);
}
fprintf(pad,"1 (%d)\n",j);
#endif // ONE
break;
}
for(int k=0;k<=j-1;k++)
{
if(s[j]==s[k])
{
#ifdef LOOP
for(p=0;p<=j-1;p++)
{
fprintf(pad,"%d->",s[p]);
}
fprintf(pad,"%d (%d)[%d]\n",s[j],j,j-k);
//j为前进总步数,j-k为闭环长
#endif // LOOP
}
if(br)
{
br=0;
break;
}
}
if(j==MAX)
{
#ifdef OVERLONG
for(p=0;p<=j-1;p++)
{
fprintf(pad,"%d->",s[p]);
}
fprintf(pad,"To Be Continued\n");
#endif
}
}
return 0;
}对100000以内的数进行分类追踪,发现至少有80723个数都回到1。至少有2073个数进入闭环。有17204个数超出int范围,它们中也会有一部分最终回到1,另一部分进入闭环,是否还有一部分真的永不重复(那意味着序列无上界)?没有数超出次数的界限。
5 亲和图的结构与闭环
到这里我们对亲和图的结构有了大致的认识。1(或0)是大多数数的归宿,如百川汇海。完全数、相亲数,亲和数链则是一少部分数的吸引子。
对1以外的任一个节点,我们可以任意有限阶数地追踪它的来源,即先求指向它的数,再求指向指向它的数的数,以此类推。对于闭环,我们也可以对它进行来源追踪,称为闭环的来源k阶展开。
10万以内的完全数只有6,28,496,8128四个。6的3阶展开为(图1)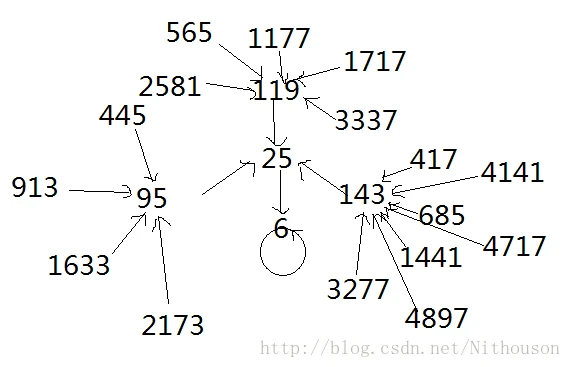
10万以内的相亲数共13对,以220和284为例作1阶展开(图2)
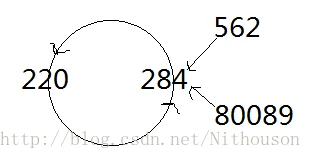
三元亲和数链在较小整数范围内没有解。值得一提的是五元亲和数链12496-14288-15472-14536-14264,五个数大小类似又都不大,用来象征奥运五环、五洲和谐再合适不过了。另一个较小的环有28元,为14316-19116-31704-47616-83328-177792-295488-629072-589786-294896-358336-418904-366556-274924-275444-243760-376736-381028-285778-152990-122410-97946-48976-45946-22976-22744-19916-17716。用程序2的LOOP模式,再加环长不小于3的条件,就能发现这个环。我还用程序2验证了:涉及10万以内数,长度不小于3,且没有数超出int范围的闭环只有以上的一个5元环和一个28元环。
6 未竟的事业
亲和图中的重大问题还有很多有待解决,如:
(1)任一点出发最终回到1或进入闭环的猜想是否正确?
(2)如何解释奇数的入度普遍多于偶数这一事实?
(3)亲和图中是否存在孤立结构(即一个顶点集,既没有从集合内指向集合外的边,又没有从集合外指向集合内的边)?
对于闭环,也有一系列问题。相亲数是否有无穷多对?两数差最小是多少,是不是26(1184,1210)?差最大是否有无穷大?三元及以上的亲和数链,是否有无穷多?
感觉上说,如果说完全数尚有规律可把握,多元的亲和数链则显得离散,有巧合的成分(只要算出的F(n)之前碰巧出现过,就成环了)。每个数因数分解性质的不同,为理论上整体把握亲和图的性质带来了困难。更大规模的计算与绘图,或许会给我们带来更多新发现。
2017年1月8日
17:39:28
