一.汉诺塔问题及其递归算法
1.问题阐述
经典汉诺塔:

外文算法书对汉诺塔问题的描述:
2.算法步骤
三阶汉诺塔问题解题步骤
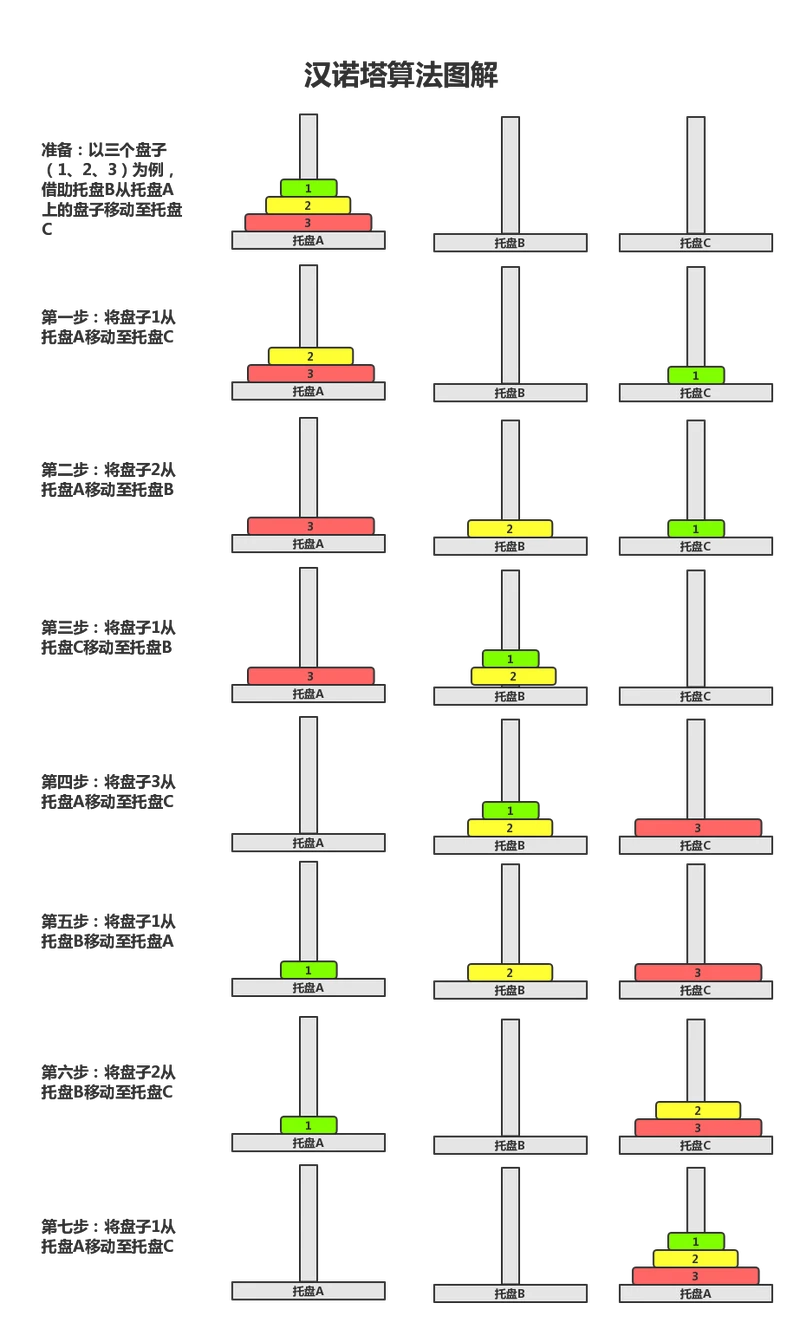
共需7步。
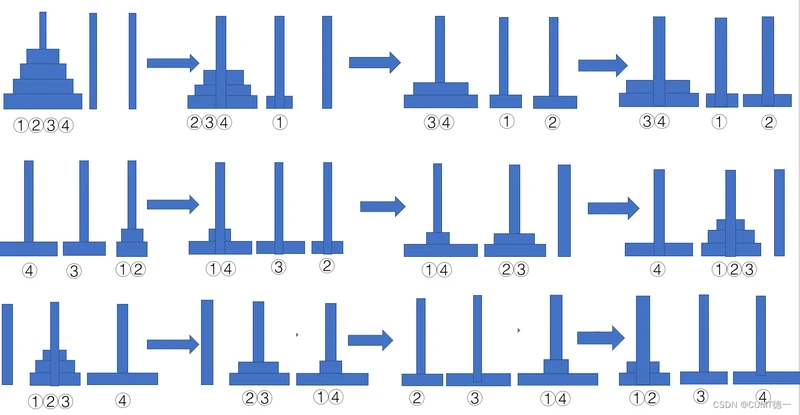
四阶汉诺塔问题解题步骤

共需15步
五阶汉诺塔问题解题步骤
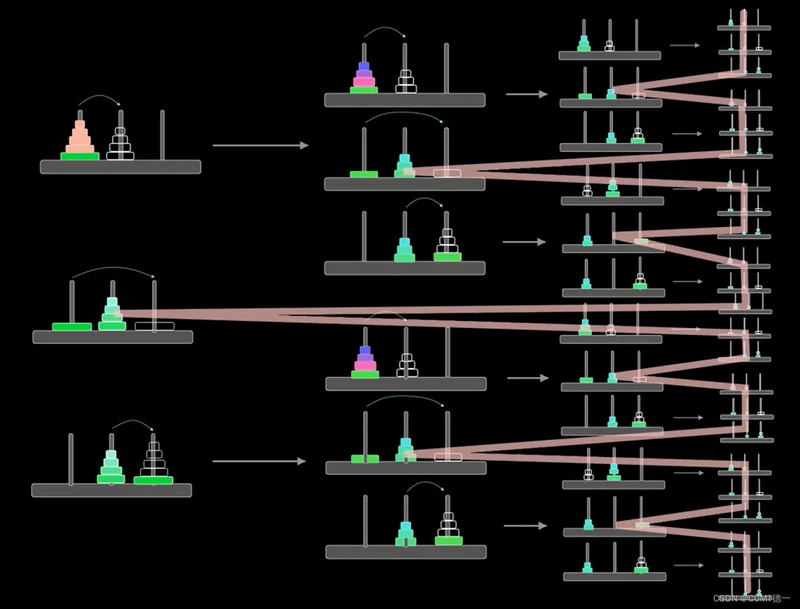
算法采用了分治的思想,利用递归的方式,完成n层汉诺塔的移动。
问题解法:
当n=1时,只要将编号为1的圆盘从柱子A直接移到柱子C上即可。
当n>1时,就需要借助另外一根柱子来移动。将n个圆盘由A移到C上可以分解为以下几个步骤:
(1) 将A柱子上的n-1个圆盘借助C柱子移到B柱子上;
(2) 把A柱子上剩下的一个圆盘从A柱子移到C柱子上;
(3) 最后将剩下的n-1个圆盘借助A柱子从B柱子移到C柱子上。
假定n是圆盘的数量,T(n)是移动n个圆盘的移动次数。
当n=1时,T(1)=1
当n=2时,T(2)=2T(1)+1
当n=3时,T(3)=2T(2)+1
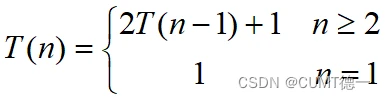
- 递归关系式:
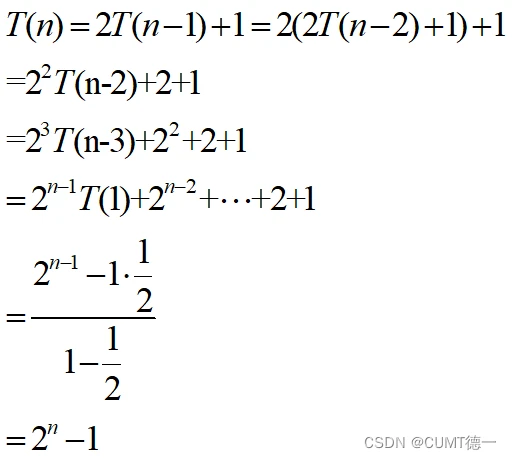
所以,n阶汉诺塔问题最少共需要2的n次方减1步
算法的时间复杂度为
![]()