图论路径搜索

对图算法有兴趣的朋友可以关注微信公众号：《 Medical与AI的故事》

原文链接：《图算法》第四章-1 路径查找和图搜索算法

图搜索（Graph Search）算法是用于在图上进行一般性发现或显式地搜索的算法。这些算法在图上找到出路径，但没有期望这些路径是在计算意义上是最优的。我们将涵盖广度优先搜索（Breadth First Search，BFS）和深度优先搜索（Deep First Search，DFS），因为它们是遍历一个图的基础算法，通常也是许多其他进一步分析的先决条件。

路径查找算法（Pathfinding）是建立在图搜索算法的基础上，它探索节点之间的路径，从一个节点开始，遍历关系，直到到达目的节点。这些算法用于识别图中的最优路由，算法可以用于诸如物流规划、最低成本呼叫或IP路由以及游戏模拟等用途。

具体来说，我们将介绍的路径查找算法包括：

最短路径（shortest path），以及它的两种变体（A*和Yen’s）：找到两个指定节点之间的最短路径
所有结对最短路径（All Pairs Shortest Path，APSP）和单源最短路径（Single Source Shortest
Path，SSSP）：用于查找所有节点对之间的最短路径，或从选定节点到所有其他所有节点的最短路径
最小生成树（Minimum Spanning Tree，MST）：用于找到一个连接树结构，在这个结构中，从指定节点访问所有节点的成本最小
随机行走（Random Walk）：它是机器学习工作流或其他图算法的一个有用的预处理/采样步骤。

在本章中，我们将解释这些算法是如何工作的，并在Spark和Neo4j中上运行示例。如果一个算法只在一个平台中可用，我们将仅提供一个示例，或者说明如何优化我们的实现。

图4-1显示了这些算法类型之间的主要区别，表4-1是对每个算法具体做什么给出了例子。
在这里插入图片描述
图4-1.路径查找和图搜索算法

表4-1.路径查找和图搜索算法概述
在这里插入图片描述
首先，让我们查看一下示例中的数据集，并介绍如何将数据导入Apache Spark和Neo4j中。对于每种算法，我们将从对算法的简短描述以及有关它如何操作的相关信息开始。大多数章节还包括有关何时使用相关算法的指导。最后，我们在每个算法部分的最后，将提供用示例代码和数据集运行的结果。

让我们开始吧！

示例数据：交通图

所有的数据网络都包含节点之间的路径，因此，图搜索和路径查找是图分析的起点。交通数据集以直观和可访问的方式说明了这些关系。本章中的示例是欧洲道路网子集的图对应的数据。你可以从本书的Github下载节点和关系文件。
表 4-2. transport-nodes.csv
在这里插入图片描述
表 4-3. transport-relationships.csv

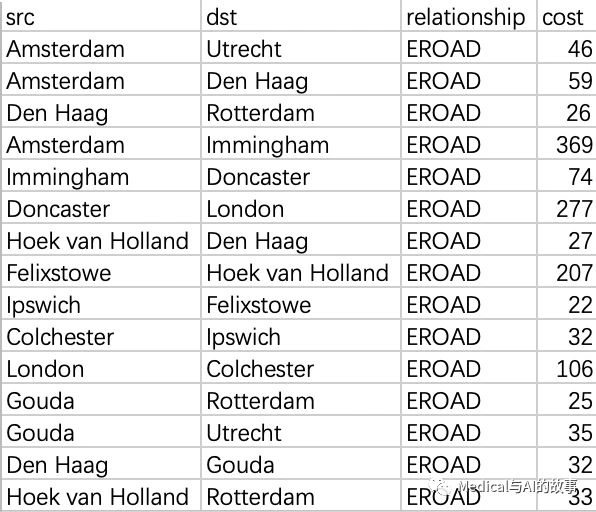
图4-2显示了我们想要构建的目标图。

图4-2.交通图
为了简单起见，我们认为图4-2中的图表是无向的，因为城市之间的大多数道路是双向的。如果我们把图当做有向的，会得到稍微不同的结果，因为会有少量的单向街，但是总体方法仍然是相似的。但是，Spark和Neo4j的算法都在有向图上操作。在这种情况下，如果我们想使用无向图（例如双向道路），有一种简单的方法可以做到：

对于Spark，我们将在transport-relationships.csv的每一行创建两个关系，一个从dst到src，另一个从src到dst。
对于Neo4j，我们将创建单个有向的关系，并在运行算法时忽略关系方向。

了解了这些基本的建模解决方法后，我们现在可以开始从示例csv文件将图加载到Spark和Neo4j中。

将数据导入Apache Spark

从Spark开始，我们将首先从Spark和GraphFrames包中导入所需的包：

from graphframes import *
from pyspark.sql.types import *

以下的函数在示例CSV文件基础上创建出一个GraphFrame

def create_transport_graph():
    base = "file:///home/retire2053/source/graph_algorithms_resources/"
    node_fields = [
        StructField("id", StringType(), True),
        StructField("latitude", FloatType(), True),
        StructField("longitude", FloatType(), True),
        StructField("population", IntegerType(), True)
    ]
    nodes = spark.read.csv(base+"data/transport-nodes.csv", header=True,
                           schema=StructType(node_fields))
    rels = spark.read.csv(base+"data/transport-relationships.csv", header=True)
    reversed_rels = (rels.withColumn("newSrc", rels.dst)
                     .withColumn("newDst", rels.src)
                     .drop("dst", "src")
                     .withColumnRenamed("newSrc", "src")
                     .withColumnRenamed("newDst", "dst")
                     .select("src", "dst", "relationship", "cost"))
    relationships = rels.union(reversed_rels)
    return GraphFrame(nodes, relationships)

以上代码上的base变量，需要替换成为具体的路径，以便于pyspark找到csv文件。

装载这些节点是很容易的，但是对于关系，我们需要一些预处理才能把每个关系创建两遍（因为要表示双向交通）。让我们调用这个函数。

g = create_transport_graph()

将数据导入Neo4j

现在是将数据导入Neo4j的时候了，用如下的Cypher语句，先导入节点。

WITH "https://github.com/neo4j-graph-analytics/book/raw/master/data" AS base
WITH base + "/transport-nodes.csv" AS uri
LOAD CSV WITH HEADERS FROM uri AS row
MERGE (place:Place {id:row.id})
SET place.latitude = toFloat(row.latitude),
place.longitude = toFloat(row.latitude),
place.population = toInteger(row.population);

以下是导入关系的语句。

WITH "https://github.com/neo4j-graph-analytics/book/raw/master/data/" AS base
WITH base + "/transport-relationships.csv" AS uri
LOAD CSV WITH HEADERS FROM uri AS row
MATCH (origin:Place {id: row.src})
MATCH (destination:Place {id: row.dst})
MERGE (origin)-[:EROAD {distance: toInteger(row.cost)}]->(destination);

虽然我们保存的是有向的关系，但是我们在本章后面内容中，将会以忽略方向的模式来执行算法。

广度优先搜索

广度优先搜索（Breadth First Search, BFS）是一种基本的图遍历算法。它从一个选定的节点开始，在一个跃点（one hop）距离处探索附近节点，然后在两个跃点（two hops）距离处访问所有节点，依此类推。

该算法最早于1959年由Edward F. Moore出版，他用它来寻找迷宫中最短的路径。然后，C.Y.Lee于1961年将其开发成一种布线算法，发表在文章An Algorithm for Path Connections and Its Applications中。

BFS是其他目标更明确的算法的基础。比如，最短路径（Shortest Path）、连接组件（Conneced Component）和紧密中心性（Closeness Centrality）都使用BFS算法。它还可以用来寻找节点之间的最短路径。

图4-3显示了如果我们执行从荷兰城市Den Haag（海牙）开始的广度优先搜索，我们访问传输图节点的顺序。城市名称旁边的数字表示访问每个节点的顺序。
在这里插入图片描述
图4-3.从Den Haag开始的广度优先搜索。节点号表示遍历的顺序。
我们先去拜访所有Den Haag的最近邻近节点，然后再去拜访邻近节点的邻近节点，直到我们跑遍了所有的关系。

Apache Spark上的广度优先搜索

Spark实现的广度优先搜索算法通过两个节点之间跃点数来寻找到两个节点之间的最短路径。你可以显式（explicitly）指明目标节点或添加要满足的条件。

例如，我们可以使用BFS函数找到第一个中等城市（按照欧洲标准），人口在10万到30万之间。

让我们首先检查哪些地方的人口符合这些标准：

(g.vertices.filter("population > 100000 and population < 300000").sort("population").show())

我们将会得到如下结果


+-----------+--------+---------+----------+
|        id |latitude|longitude|population|
+-----------+--------+---------+----------+
|cColchester|51.88921|  0.90421|   c104390|
|   Ipswich |52.05917|  1.15545|    133384|
+-----------+--------+---------+----------+

只有两个地方符合我们的标准，我们在广度优先搜索中会率先到达Ipswich。
以下代码用来查找从Den Haag到中等城市的最短路径：

from_expr = "id='Den Haag'"
to_expr = "population > 100000 and population < 300000 and id <> 'Den Haag'"
result = g.bfs(from_expr, to_expr)

结果包含描述两个城市之间的节点和关系的列。我们可以运行以下代码来查看返回的列列表：

print(result.columns)

这是我们将看到的输出：

['from', 'e0', 'v1', 'e1', 'v2', 'e2', 'to']

以e开头的列表示关系（边），以v开头的列表示节点（顶点）。我们只对节点感兴趣，所以我们过滤掉从生成的DataFrame中以e开头的任何列：

columns = [column for column in result.columns if not column.startswith("e")]
result.select(columns).show()

如果我们在PySpark中运行代码，我们将看到这个输出：

+--------------------+--------------------+--------------------+--------------------+
|                from|                  v1|                  v2|                  to|
+--------------------+--------------------+--------------------+--------------------+
|[Den Haag, 52.078...|[Hoek van Holland...|[Felixstowe, 51.9...|[Ipswich, 52.0591...|
+--------------------+--------------------+--------------------+--------------------+

如预期，bfs算法返回Ipswich！记住，当找到第一个匹配时，这个函数是满足的，如图4-3所示，ipswich在Colchester之前被遍历到。

深度优先搜索

深度优先搜索（Deep First Search，DFS）是另一种基本的图遍历算法。它从一个选定的节点开始，选择它的一个邻近节点，然后在回溯之前沿着该路径尽可能地进行遍历。

DFS最初是由法国数学家Charles Pierre Tremaux发明的用来一种解决迷宫的策略。这是对分析模拟场景建模中所有可能路径非常有用的工具。

如果我们执行从Den Haag开始的DFS，图4-4显示了访问交通图节点的顺序。
在这里插入图片描述
图4-4.深度优先搜索从Den Haag开始。节点号表示遍历的顺序。

注意节点顺序与BFS的区别。对于这个DFS，我们首先从Den Haag遍历到Amsterdam，然后能够到达图中的每个其他节点，而不需要回溯！

我们可以看到搜索算法是如何在图中进行移动的。现在，让我们看看路径查找的算法，它们根据跃点数或权重找到最经济的路径。权重可以是任何度量的量，例如时间、距离、容量或成本。

注意，在Spark和Neo4j上均没有深度优先搜索的代码示例。

两种特殊路径/环

图分析有两种值得注意的特殊路径。欧拉路径（Eulerian path）是每个关系访问一次的路径，另一个是汉密尔顿路径（Hamiltonian path），它是每个节点都访问一次的特殊路径。如果你在同一节点开始和结束，它被认为是一个环形旅行，这种路径可能同时是欧拉路径和汉密尔顿路径。图4-5展示了一些例子。

在这里插入图片描述
图4-5.欧拉环和汉密尔顿环是具有特殊的历史意义的路径。

第一章的哥尼斯堡七桥问题是在寻找欧拉环。很容易想到，欧拉环可以适用于如定向除雪或邮件传递等其他场景。不仅仅如此，欧拉路径也被其他算法用于处理树结构中的数据，并且在数学上比其他路径更容易研究。
汉密尔顿环最广为人知的是它被用于商旅问题（Traveling Salesman Problem，TSP）。TSP是这样的：对于一个销售员来说，访问他们指定的每个城市并返回原来的城市，最短路线是什么？尽管看起来与欧拉巡演相似，但在近似替换的情况下，TSP的计算量更大。它被用于各种各样的计划、物流和优化问题中。

最短路径

最短路径（Shortest Path）算法计算一对节点之间的最短（加权）路径。它在和用户产生交互的动态工作流很有用，因为它可以实时工作。

路径查找算法的历史可以追溯到19世纪，被认为是一个经典的图论问题。它在20世纪50年代早期的可替换路由问题中体现突出的作用；也就是说，如果最短的路由被阻塞，则找到第二条最短的路由。1956年，Edsger Dijkstra发明了这些最著名的算法。

Dijkstra的最短路径算法首先找到从起始节点到直接连接节点的最小权重关系。它跟踪这些权重并移动到“最近”节点。然后，它执行相同的计算，只不过权重的累积是从初始节点开始算的。算法继续持续迭代，就可以评估从初始节点的一个累积权重的“波浪”，并始终选择要前进的最小加权累积路径，直到到达目标节点。
在这里插入图片描述
在图分析中，当描述关系和路径时，你会注意到“权重”（weight）、“成本”（cost）、“距离”（distance）和“跃点数”（hop）等术语的使用。“权重”是关系的特定属性的数值。“成本”（cost）的用法与此类似，但在考虑路径的总权重时，我们会更经常看到它。
“距离”（distance）通常在算法中用作关系属性的名称，表示一对节点之间的遍历成本。并不一定是非要在实际物理测量中才这么用。跃点数通常用于表示两个节点之间经历的关系数。你可能会看到其中一些术语组合在一起，如“到伦敦有五个跃点的距离”或“这是距离的最低成本”。

最短路径算法的使用场景

利用最短路径算法可以在一对节点之间找到最佳路径，衡量的指标是跃点数或者任何权重值。例如，它可以提供关于分离程度、点之间短距离或最小扩展路径的实际答案。你也可以使用这个算法简单地探索特别节点之间的连接。

使用场景可以包括：

确定位置之间的方向。在手机地图软件（比如谷歌地图）用最短路径算法或者某些变体算法来提供驾驶导航。
发现社交网络中人之间的离散距离。比如，当你看到某人在社交网站上的简介时，它会显示出图中你离他之间有多少人，也会显示你们之间的共同联系人。
找到一个演员和Kevin Bacon所出现的电影之间的逻辑距离。在Oracle of Bacon website. The Erd.s Number Project 提供了一个“和Paul Erdos的合作网络”的类似功能，其中Paul
Erdos是20世纪最有影响力的数学家之一。

在这里插入图片描述
Dijkstra的算法不支持负的权重。该算法假定，在路径上增加一个关系，只会让路径变得更长。如果有负权重，这个假设会被破坏掉。

Neo4j上的最短路径算法

Neo4j图算法库有一个内置的存储过程，我们可以使用它来计算无权重和有权重的最短路径。让我们先学习如何计算无权重的最短路径。

所有Neo4j的最短路径算法都假定基础图是无向的。你可以通过传递参数 direction: “OUTGOING” 或者direction: "INCOMING"来更改默认设置。Outgoing代表了出链，Incoming代表了入链。

为了让Neo4j的最短路径算法忽略权重，我们需要将空值作为过程的第三个参数传递，这表明在执行算法时我们不想考虑权重属性。然后，算法将假定每个关系的默认权重为1.0：

MATCH (source:Place {id: "Amsterdam"}),
(destination:Place {id: "London"})
CALL algo.shortestPath.stream(source, destination, null)
YIELD nodeId, cost
RETURN algo.getNodeById(nodeId).id AS place, cost

此查询返回以下输出：

+---------------------+
| place        | cost |
+---------------------+
| "Amsterdam" | 0.0  |
|  "Immingham" | 1.0  |
| "Doncaster" | 2.0  |
|  "London"    | 3.0  |
+---------------------+

这里的成本是累积的关系数量（或跃点数量）。这与我们在Spark中使用广度优先搜索看到的相同。

我们甚至可以通过编写一些带后置处理的Cypher来计算遵循这条路径的总距离。以下过程计算最短的无权重路径，然后计算出该路径的实际成本：

MATCH (source:Place {id: "Amsterdam"}),
(destination:Place {id: "London"})
CALL algo.shortestPath.stream(source, destination, null)
YIELD nodeId, cost
WITH collect(algo.getNodeById(nodeId)) AS path
UNWIND range(0, size(path)-1) AS index
WITH path[index] AS current, path[index+1] AS next
WITH current, next, [(current)-[r:EROAD]-(next) | r.distance][0] AS distance
WITH collect({current: current, next:next, distance: distance}) AS stops
UNWIND range(0, size(stops)-1) AS index
WITH stops[index] AS location, stops, index
RETURN location.current.id AS place,
reduce(acc=0.0,
distance in [stop in stops[0..index] | stop.distance] |
acc + distance) AS cost;

如果前面的代码感觉有点笨拙，那么请注意，最复杂的部分是如何处理数据，以包括整个遍历的成本。这有助于我们在需要累积路径成本时记住这一点。查询返回以下结果：

+----------------------+
| place        | cost  |
+----------------------+
| "Amsterdam"   | 0.0   |
| "Immingham"   | 369.0 |
| "Doncaster"   | 443.0 |
| "London"      | 720.0 |
+----------------------+

图4-6显示了从Amsterdam到London的无权重的最短路径，使我们通过最少的城市。总成本是720公里。
在这里插入图片描述
图4-6.Amsterdam和London之间的无权重最短路径，会选择访问节点数最少的路线，在地铁系统等需要较少站点的情况下可能非常有用。然而，在驾驶场景中，我们可能更感兴趣的是使用最短权重路径的总成本。

Neo4j上的加权重最短路径

我们可以执行有权重的最短路径算法，找到Amsterdam和London之间的最短路径，如下所示：

MATCH (source:Place {id: "Amsterdam"}),
(destination:Place {id: "London"})
CALL algo.shortestPath.stream(source, destination, "distance")
YIELD nodeId, cost
RETURN algo.getNodeById(nodeId).id AS place, cost

传递给此算法的参数为：
source
最短路径搜索开始的节点
destination
最短路径的终点
distance
表示一对节点之间遍历成本的关系属性的名称。
成本是两个地点之间的公里数。查询返回以下结果：

+----------------------------+
| place              | cost  |
+----------------------------+
| "Amsterdam"        | 0.0   |
| "Den Haag"         | 59.0  |
| "Hoek van Holland" | 86.0  |
| "Felixstowe"       | 293.0 |
| "Ipswich"          | 315.0 |
| "Colchester"       | 347.0 |
| "London"           | 453.0 |
+----------------------------+

最快的路线是通过Den Haag，Hoek van Holland，Felixstowe，Ipswich和Colchester！显示的成本是我们在城市中前进时的累积的距离总量。首先，我们从Amsterdam去Den Haag，成本是59km。然后我们从Den Haag到Hoek van Holland，累计花费86km，以此类推。最后，我们从Colchester到达London，总共花费453km。

请记住，无权重的最短路径的总成本为720公里，因此在计算最短路径时，我们可以考虑权重，从而节省267公里。

Apache Spark上的加权最短路径

在Apache Spark的广度优先搜索中，我们学习了如何找到两个节点之间的最短路径。这个最短路径是基于跃点数的，因此与加权最短路径有所不同，加权最短路径这将告诉我们城市之间最短的总距离。

如果我们想要找到最短的权重路径（在本例中是距离），我们需要使用cost这个属性，它用于各种类型的权重计算。这个选项不能与GraphFrame一起使用，因此我们需要使用它的aggregateMessages框架编写我们自己的加权最短路径版本。虽然Spark的大多数算法示例都使用了从库中调用算法的简单过程，但是我们可以选择编写自己的函数。有关AggregateMessages的更多信息，请参阅Message passing via AggregateMessages的AggregateMessages部分。
在这里插入图片描述
如果可行的话，我们建议利用现有的、经过测试的库。编写我们自己的函数，特别是对于更复杂的算法，需要对数据和计算有更深的理解。下面的示例应被视为参考实现，并需要在运行于更大的数据集之前进行优化。那些对编写自己的函数不感兴趣的人可以跳过这个例子。
在创建函数之前，我们将导入一些将要使用的库：

from graphframes.lib import AggregateMessages as AM
from pyspark.sql import functions as F

Aggregate_Message模块是GraphFrames库的一部分，包含一些有用的helper函数。现在我们来编写函数。我们首先创建一个用户定义函数，用于构建源和目标之间的路径：

add_path_udf = F.udf(lambda path, id: path + [id], ArrayType(StringType()))

现在，对于主函数，它计算从原点开始的最短路径，并在访问目的地后立即返回：

def shortest_path(g, origin, destination, column_name="cost"):
    if g.vertices.filter(g.vertices.id == destination).count() == 0:
        return (spark.createDataFrame(sc.emptyRDD(), g.vertices.schema)
                .withColumn("path", F.array()))
    vertices = (g.vertices.withColumn("visited", F.lit(False))
                .withColumn("distance", F.when(g.vertices["id"] == origin, 0)
                            .otherwise(float("inf")))
                .withColumn("path", F.array()))
    cached_vertices = AM.getCachedDataFrame(vertices)
    g2 = GraphFrame(cached_vertices, g.edges)
    
    while g2.vertices.filter('visited == False').first():
        current_node_id = g2.vertices.filter('visited == False').sort("distance").first().id
        msg_distance = AM.edge[column_name] + AM.src['distance']
        msg_path = add_path_udf(AM.src["path"], AM.src["id"])
        msg_for_dst = F.when(AM.src['id'] == current_node_id,
                             F.struct(msg_distance, msg_path))
        new_distances = g2.aggregateMessages(F.min(AM.msg).alias("aggMess"),
                                             sendToDst=msg_for_dst)
        new_visited_col = F.when(g2.vertices.visited | (g2.vertices.id == current_node_id),True).otherwise(False)
        new_distance_col = F.when(new_distances["aggMess"].isNotNull() &
                                  (new_distances.aggMess["col1"]
                                   < g2.vertices.distance),
                                  new_distances.aggMess["col1"]).otherwise(g2.vertices.distance)
                                  
        new_path_col = F.when(new_distances["aggMess"].isNotNull() & (new_distances.aggMess["col1"]< g2.vertices.distance), new_distances.aggMess["col2"]
                              .cast("array<string>")).otherwise(g2.vertices.path)
        new_vertices = (g2.vertices.join(new_distances, on="id",
        how="left_outer")
                                         .drop(new_distances["id"])
                                         .withColumn("visited", new_visited_col)
                                         .withColumn("newDistance", new_distance_col)
                                         .withColumn("newPath", new_path_col)
                                         .drop("aggMess", "distance", "path")
                                         .withColumnRenamed('newDistance', 'distance')
                                         .withColumnRenamed('newPath', 'path'))
        cached_new_vertices = AM.getCachedDataFrame(new_vertices)
        g2 = GraphFrame(cached_new_vertices, g2.edges)
        if g2.vertices.filter(g2.vertices.id == destination).first().visited:
            return (g2.vertices.filter(g2.vertices.id == destination)
                    .withColumn("newPath", add_path_udf("path", "id"))
                    .drop("visited", "path")
                    .withColumnRenamed("newPath", "path"))
    return (spark.createDataFrame(sc.emptyRDD(), g.vertices.schema)
            .withColumn("path", F.array()))

在这里插入图片描述
如果我们在函数中存储对任何DataFrame的引用，我们需要使用AM.getCachedDataFrame函数来缓存它们，否则在执行过程中会遇到内存泄漏。在最短路径函数中，我们使用这个函数来缓存顶点和新的顶点DataFrame。

如果我们想找到Amsterdam和Colchester之间最短的路径，我们可以这样调用这个函数：

result = shortest_path(g, "Amsterdam", "Colchester", "cost")
result.select("id", "distance", "path").show(truncate=False)

确实，经过一段时间的执行（示例代码的运行效率比较低），结果如下：

+----------+--------+------------------------------------------------------------------------+
|id        |distance|path                                                                    |
+----------+--------+------------------------------------------------------------------------+
|Colchester|347.0   |[Amsterdam, Den Haag, Hoek van Holland, Felixstowe, Ipswich, Colchester]|
+----------+--------+------------------------------------------------------------------------+

Amsterdam与Colchester之间最短路径的总距离为347公里，途经Den Haag、Hoek van Holland、Felixstowe和Ipswich。相比之下，我们使用广度优先搜索算法（参见图4-4）计算出的位置之间关系数量方面的最短路径则会经过Immingham、Doncaster和London。