1. 简介
我们在最灰度图做二值化时,需要设定一个分割阈值,我们并没有一个万能的阈值。而Otsu大津算法则是根据灰度图本身的信息,自动确定最佳阈值,实现以最佳阈值对灰度图进行二值化。
需要注意的是,大津算法并不是直接进行二值化处理,而是得到一个整型数字,也即阈值,我们得到阈值再进行二值化。
2. 原理
我们对图片进行二值化时,是希望将图片分割成两部分,暂且称之为前景和背景:

一般情况下,我们将我们感兴趣的部分称为前景,比如图中的人;对于不感兴趣的称为背景。
大津算法的思想是比较简单的,我们认为分为的前景和背景之间差异是较大的,而前景部分中的像素是相似的,背景部分中的像素是相似的:同一类中差异小,不同类中差异大。那么如果存在一个阈值,使得图像分为了前景和背景,应当符合同一类中差异最小,不同类中差异最大,这个值就是最佳阈值。根据这个最佳阈值分割的图像效果应当是最好的(即将前景和背景彻底分割开)。
那么所谓的“差异”如何表示?其实就是用方差来表示:如果单个的数据其越偏离于中心,那么,其方差值也就越大。如果同一类中方差越小,那么表示同一类中差异也小;不同类之间方差越大,表示不同类中差异越大。
方差:
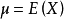
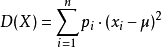
3. 详细步骤

第6步中求得方差是类间方差:
f:表示front,前景
b:表示back,背景
p
f
p_f
pf:前景像素个数/总个数,即前景占总图的比率
p
b
p_b
pb:背景像素个数/总个数,即背景占总图的比率
M
f
M_f
Mf:前景所有像素灰度值均值
M
b
M_b
Mb:背景所有像素灰度值均值
M
M
M:所有像素灰度值均值
一个典型的2个类的方差求法
实际上图像的像素个数、每个像素的值都是已知的,唯一的变量是
T
0
T_0
T0,所以实际上是求当
δ
2
δ^2
δ2最大时,
T
0
T_0
T0的值,典型的求导,反正只有255级,直接遍历,保存方差最大和对应的阈值即可
