矩阵乘法
满足结合率、分配率,但不满足交换率
-
矩阵 Am*n
有 m 行,n 列
-
矩阵 Bn*s
有 n 行,s 列
B 的行数与 A 的列数相等,这是矩阵可以相乘的前提
B 的列数可以任意
-
相乘的积矩阵 Cm*s
积C的行数 = A 的行数 m
积C的列数 = B 的列数 s
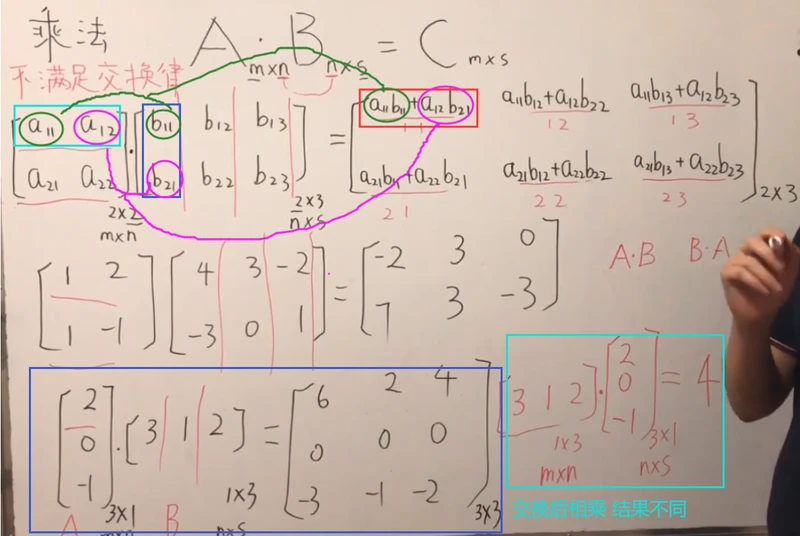
C[ i,j ] 的值等于 A 中第 i 行的值,分别与 B 中第 j 列的值相乘,再相加
如下图:
C[2,3] = A[2,1] * B[1,3] + A[2,2] * B[2,3]
系数矩阵

矩阵乘法 满足结合率、分配率,但不满足交换率 矩阵 Am*n 有 m 行,n 列 矩阵 Bn*s 有 n 行,s 列 B 的行数与 A 的列数相等 ,这是矩阵可以相乘的前提 B 的列数可以任意 相乘的积矩阵 Cm*s 积C的行数 = A 的行数 m
满足结合率、分配率,但不满足交换率
矩阵 Am*n
有 m 行,n 列
矩阵 Bn*s
有 n 行,s 列
B 的行数与 A 的列数相等,这是矩阵可以相乘的前提
B 的列数可以任意
相乘的积矩阵 Cm*s
积C的行数 = A 的行数 m
积C的列数 = B 的列数 s
C[ i,j ] 的值等于 A 中第 i 行的值,分别与 B 中第 j 列的值相乘,再相加
如下图:
C[2,3] = A[2,1] * B[1,3] + A[2,2] * B[2,3]

