PaddlePaddle 深度学习实战(第一部分)
PaddlePaddle 深度学习实战(第二部分)
PaddlePaddle 深度学习实战(第三部分)
PaddlePaddle 深度学习实战(第四部分)
PaddlePaddle 深度学习实战(第五部分)
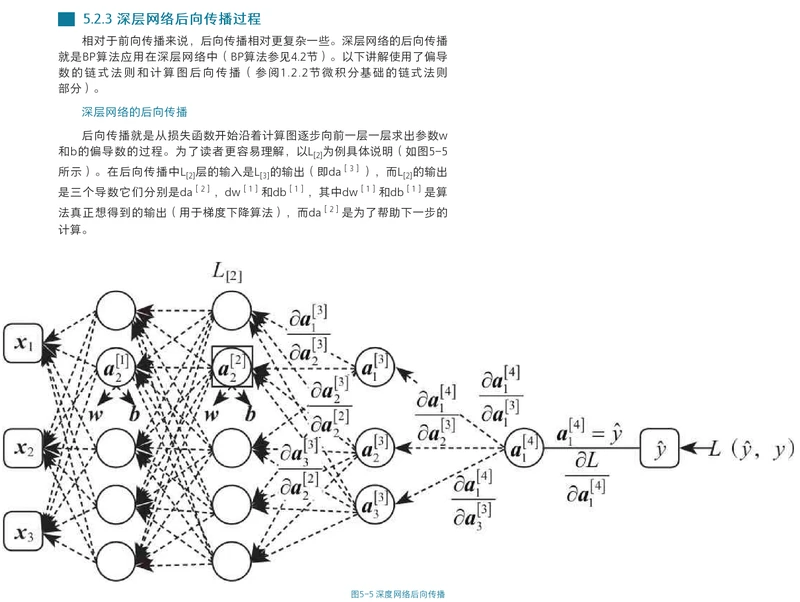
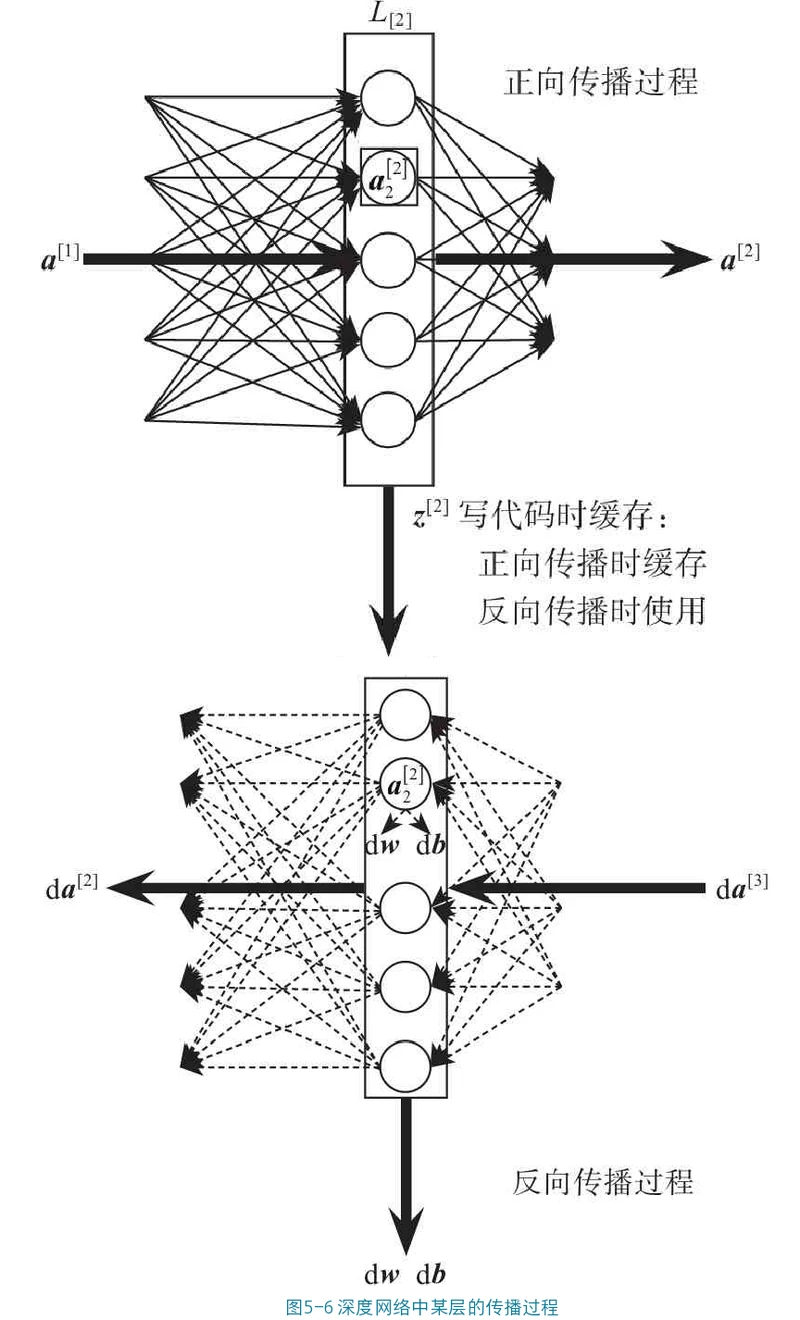
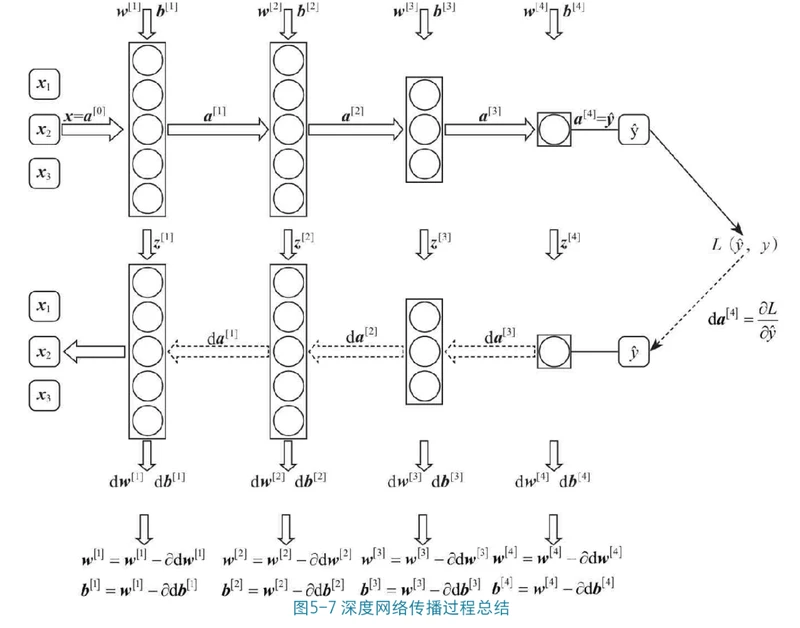
深层神经网络
深层神经网络:前向传播、反向传播、梯度下降的numpy实现+PaddlePaddle实现








import h5py
import matplotlib.pyplot as plt
import numpy as np
#传入参数layer = [12288, 20, 7, 5, 1],即[输入层节点数, 隐藏层1节点数, 隐藏层2节点数, 隐藏层3节点数, 输出层节点数]
def initialize_parameters(layer):
"""
初始化参数
Args: layer:各层所包含的节点数
Return: parameters:参数,包括w和b
"""
np.random.seed(2) # 设置随机种子
parameters = {}
# 随机初始化参数w,b初始化为0
for i in range(len(layer) - 1):
"""
第一隐藏层:w0:(20, 12288) b0:(20, 1)
第二隐藏层:w1:(7, 20) b1:(7, 1)
第三隐藏层:w2:(5, 7) b2:(5, 1)
输出层: w3:(1, 5) b3:(1, 1)
"""
parameters['w' + str(i)] = np.random.randn(layer[i + 1], layer[i]) / np.sqrt(layer[i])
parameters['b' + str(i)] = np.random.randn(layer[i + 1], 1) * 0
return parameters
def forward_calculate(X, parameters):
"""
前向计算
Args:
X: features
parameters: 参数w和b
Return:
A: 包含输入x和各层输出值a,len(A)值为5,包含输入层x+3层隐藏层输出值a+输出层输出值a
Z: 包含隐藏层和输出层的中间值z,len(Z)值为4,包含3层隐藏层中间值z+输出层中间值z
"""
A = []
A.append(X) #输入层的值
Z = []
length = int(len(parameters) / 2) #len(parameters)值为8,length值为4
# 计算隐藏层,此处计算3层隐藏层
for i in range(length - 1):
# 加权、偏移,即第一步线性函数wx+b
z = np.dot(parameters['w' + str(i)], A[i]) + parameters['b' + str(i)]
# 隐藏层输出的中间值,即线性函数结果值
Z.append(z)
# 激活,即第二步非线性函数
a = np.maximum(0, z)
#把当前这一隐藏层输出的非线性函数结果值作为下一隐藏层的输入
A.append(a)
# 计算输出层,即第一步线性函数wx+b
z = np.dot(parameters['w' + str(length - 1)], A[length - 1]) + parameters['b' + str(length - 1)]
# 输出层输出的中间值,即线性函数结果值
Z.append(z)
# 激活,即第二步非线性函数sigmoid
a = 1. / (1 + np.exp(-z))
# 输出层的输出值
A.append(a)
#len(A)值为5,包含输入层x+3层隐藏层输出值a+输出层输出值a。len(Z)值为4,包含3层隐藏层中间值z+输出层中间值z。
return A, Z

def calculate_cost(A, Y):
"""
计算Cost
Args:
A: 存储输入值和各层输出值
Y: 真实值
Return:
cost: 成本cost
"""
m = Y.shape[1] # 样本个数,Y为真实值
Y_out = A[len(A) - 1] # 取模型输出值,即模型的预测值
# 计算成本,此处使用交叉熵损失函数multi_binary_label_cross_entropy_cost
probability = np.multiply(np.log(Y_out), Y) + np.multiply(np.log(1 - Y_out), 1 - Y)
cost = -1. / m * np.sum(probability)
# 确保维度的正确性。squeeze可以对矩阵和list进行压缩/降维。
cost = np.squeeze(cost)
return cost
def update_parameters(p, dp, learning_rate):
"""
更新参数w、b
Args:
p: 参数w、b
dp: 该参数w/b的梯度
learning_rate: 学习步长/学习率
Return:
更新后的参数
"""
return p - learning_rate * dp
def backward_calculate(A, Z, parameters, Y, learning_rate):
"""
后向计算
Args:
A: 包含输入x和各层输出值a
Z: 包含隐藏层和输出层的中间值z
parameters: 参数包括w,b
Y: 标签
learning_rate: 学习步长
Return:
parameters: 更新后的参数
"""
#len(A)值为5,包含输入层x+3层隐藏层输出值a+输出层输出值a。len(Z)值为4,包含3层隐藏层中间值z+输出层中间值z。
m = A[0].shape[1] #输入层的样本数
length = int(len(parameters) / 2) #len(parameters)值为8,length值为4
"""
反向计算:计算输出层的输出值a的导数da、输出层的中间值z的导数dz,用于帮助下一步继续反向计算。
输出值指该层第二步的非线性函数的结果值a,中间值指该层的第一步线性函数的结果值z。
da = - (真实值Y/模型预测值) - ((1 - 真实值Y)/(1 - 模型预测值))
dz = 模型预测值 - 真实值Y
len(A)值为5,包含输入层x+3层隐藏层输出值a+输出层输出值a,A[4]为模型预测值,np.divide(a,b)表示a除以b
"""
# 计算模型最终输出层的输出值a的导数 da = - (真实值Y/模型预测值) - ((1 - 真实值Y)/(1 - 模型预测值))
da = - (np.divide(Y, A[length]) - np.divide(1 - Y, 1 - A[length]))
# 计算输出层的中间值z的导数 dz = 模型预测值 - 真实值Y。A[4]为模型预测值。
dz = A[length] - Y
# 反向计算:计算隐藏层的导数dw、db。length值为4,所遍历的i值分别为1/2/3。
for i in range(1, length):
"""
1.计算每层隐藏层输出值a的导数da、每层隐藏层的中间值z的导数dz。
2.输出值指该层第二步的非线性函数的结果值a,中间值指该层的第一步线性函数的结果值z。
第一隐藏层:w0:(20, 12288) b0:(20, 1)
第二隐藏层:w1:(7, 20) b1:(7, 1)
第三隐藏层:w2:(5, 7) b2:(5, 1)
输出层: w3:(1, 5) b3:(1, 1)
3.第三层隐藏层:
1.第三层隐藏层 输出值a的导数da
da = 输出层w3.T * 输出层dz。
根据 输出层中间值z = 输出层权重w * 输出层输入数据。其中输出层输入数据为第三层隐藏层输出值a,即反向推导根据输出和权重求输入。
2.第三层隐藏层 中间值z的导数dz
dz = da:把第二步非线性函数的输出值a的梯度值da赋值给第一步线性函数输出的中间值z的梯度dz
dz[Z[2] <= 0] = 0:
Z[2]为第三隐藏层中间值z,Z[2]<=0 表示把中间值z中小于等于0的值转换为True,大于0的值转换为False,最终得出[True ... False]。
dz[[True ... False]]=0 表示把dz中对应索引上为True的值都转换为0,对应索引上为False的值则保持不变,
即把dz中小于等于0的值转换为0,大于0的值则保持不变,相当于ReLU函数y=max(0,x)的作用把小于等于0的值都转换为0返回。
根据“f(第三层隐藏层中间值z) = max(0,z) = 第三层隐藏层输出值a”反推导得出第三层隐藏层中间值z的导数dz。
4.第二层隐藏层:
1.第二层隐藏层 输出值a的导数da
da = 第三层隐藏层w2.T * 第三层隐藏层dz。
根据 第三层隐藏层中间值z = 第三层隐藏层权重w * 第三层隐藏层输入数据。
其中第三层隐藏层输入数据为第二层隐藏层输出值a,即反向推导根据输出和权重求输入。
2.第二层隐藏层 中间值z的导数dz
dz = da:把第二步非线性函数的输出值a的梯度值da赋值给第一步线性函数输出的中间值z的梯度dz
dz[Z[1] <= 0] = 0:
Z[1]为第二隐藏层中间值z,Z[1]<=0 表示把中间值z中小于等于0的值转换为True,大于0的值转换为False,最终得出[True ... False]。
dz[[True ... False]]=0 表示把dz中对应索引上为True的值都转换为0,对应索引上为False的值则保持不变,
即把dz中小于等于0的值转换为0,大于0的值则保持不变,相当于ReLU函数y=max(0,x)的作用把小于等于0的值都转换为0返回。
根据“f(第二层隐藏层中间值z) = max(0,z) = 第二层隐藏层输出值a”反推导得出第二层隐藏层中间值z的导数dz。
5.第一层隐藏层:
1.第一层隐藏层 输出值a的导数da
da = 第二层隐藏层w1.T * 第二层隐藏层dz。
根据 第二层隐藏层中间值z = 第二层隐藏层权重w * 第二层隐藏层输入数据。
其中第二层隐藏层输入数据为第一层隐藏层输出值a,即反向推导根据输出和权重求输入。
2.第一层隐藏层 中间值z的导数dz
dz = da:把第二步非线性函数的输出值a的梯度值da赋值给第一步线性函数输出的中间值z的梯度dz
dz[Z[0] <= 0] = 0:
Z[0]为第一隐藏层中间值z,Z[0]<=0 表示把中间值z中小于等于0的值转换为True,大于0的值转换为False,最终得出[True ... False]。
dz[[True ... False]]=0 表示把dz中对应索引上为True的值都转换为0,对应索引上为False的值则保持不变,
即把dz中小于等于0的值转换为0,大于0的值则保持不变,相当于ReLU函数y=max(0,x)的作用把小于等于0的值都转换为0返回。
根据“f(第一层隐藏层中间值z) = max(0,z) = 第一层隐藏层输出值a”反推导得出第一层隐藏层中间值z的导数dz。
"""
da = np.dot(parameters['w' + str(length - i)].T, dz)
dz = da
dz[Z[length - i - 1] <= 0] = 0
"""
len(A)值为5,包含输入层x+3层隐藏层输出值a+输出层输出值a。
len(Z)值为4,包含3层隐藏层中间值z+输出层中间值z。
第三层隐藏层:
dw=dot(dz,A[2].T)/m。A[2]为第二层隐藏层输出值a,即第三层隐藏层第一步线性函数的输入数据为第二层隐藏层输出值a。
db=dot(sum(dz))/m
第二层隐藏层:
dw=dot(dz,A[1].T)/m。A[1]为第一层隐藏层输出值a,即第二层隐藏层第一步线性函数的输入数据为第一层隐藏层输出值a。
db=dot(sum(dz))/m
第一层隐藏层:
dw=dot(dz,A[0].T)/m。A[0]为输入层x,即第一层隐藏层第一步线性函数的输入数据为输入层x。
db=dot(sum(dz))/m
"""
#计算参数w、b的梯度值
dw = 1. / m * np.dot(dz, A[length - i - 1].T)
db = 1. / m * np.sum(dz, axis=1, keepdims=True)
#更新参数w、b规则:w -= learning_rate学习率 * dw梯度值。b -= learning_rate学习率 * db梯度值。
parameters['w' + str(length - i - 1)] = update_parameters(parameters['w' + str(length - i - 1)], dw, learning_rate)
parameters['b' + str(length - i - 1)] = update_parameters(parameters['b' + str(length - i - 1)], db, learning_rate)
return parameters
def plot_costs(costs, learning_rate):
"""
把cost图形化输出
Args:
costs: 训练迭代过程中的cost
learning_rate: 学习步长
Return:
"""
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('Iterations (per hundreds)')
plt.title("learning rate =" + str(learning_rate))
plt.show()
plt.savefig('costs.png')
def deep_neural_network(X, Y, layer, iteration_nums, learning_rate=0.0075):
"""
深层神经网络模型计算(包含前向计算和后向计算)
Args:
X: 输入值
Y: 真实值
layer: 各层大小
iteration_nums: 迭代次数
learning_rate: 学习率
Return:
parameters: 模型训练所得参数,用于预测
"""
# np.random.seed(1)
costs = []
# 参数初始化
parameters = initialize_parameters(layer)
# 训练
for i in range(0, iteration_nums):
# 正向计算
# len(A)值为5,包含输入层x+3层隐藏层输出值a+输出层输出值a。
# len(Z)值为4,包含3层隐藏层中间值z+输出层中间值z。
A, Z = forward_calculate(X, parameters)
# 计算成本函数
Cost = calculate_cost(A, Y)
# 反向计算并更新参数
parameters = backward_calculate(A, Z, parameters, Y, learning_rate)
# 每100次训练打印一次成本函数
if i % 100 == 0:
print "Cost after iteration %i: %f" % (i, Cost)
costs.append(Cost)
# plot_costs(costs, learning_rate)
return parameters
def calc_accuracy(predictions, Y):
"""
准确率计算
Args:
predictions: 预测结果
Y: 标签即label
Return:
accuracy: 计算准确率
"""
Y = np.squeeze(Y)
right = 0
for i in range(len(predictions)):
if predictions[i] == Y[i]:
right += 1
accuracy = (right / float(len(predictions))) * 100
return accuracy
def predict_image(parameters, X, Y):
"""
使用模型进行预测来预测图片是否为猫(1 cat or 0 non-cat)
Args:
parameters: 包含权值和偏移量
X: 数据,形状为(px_num * px_num * 3, number of examples)
Y: 标签
Return:
accuracy: 准确率
"""
# m为数据个数
m = X.shape[1]
A = []
A.append(X)
Z = []
predictions = []
# 预测结果,即前向传播过程
A, Z = forward_calculate(X, parameters)
# 取输出值Y_out,即A的最后一组数
Y_out = A[len(A) - 1]
# 将连续值Y_out转化为二分类结果0或1
for i in range(m):
if Y_out[0, i] >= 0.5:
predictions.append(1)
elif Y_out[0, i] < 0.5:
predictions.append(0)
return calc_accuracy(predictions, Y)
def load_data_sets():
"""
用于从两个.h5文件中分别加载训练数据和测试数据
Return:
train_x_ori: 原始训练数据集
train_y: 原始训练数据标签
test_x_ori: 原始测试数据集
test_y: 原始测试数据标签
classes(cat/non-cat): 分类list
"""
train_data = h5py.File('datasets/train_images.h5', "r")
# train images features
train_x_ori = np.array(train_data["train_set_x"][:])
# train images labels
train_y_ori = np.array(train_data["train_set_y"][:])
test_data = h5py.File('datasets/test_images.h5', "r")
# test images features
test_x_ori = np.array(test_data["test_set_x"][:])
# test images labels
test_y_ori = np.array(test_data["test_set_y"][:])
# the list of classes
classes = np.array(test_data["list_classes"][:])
train_y_ori = train_y_ori.reshape((1, train_y_ori.shape[0]))
test_y_ori = test_y_ori.reshape((1, test_y_ori.shape[0]))
result = [train_x_ori, train_y_ori, test_x_ori,test_y_ori, classes]
return result
import utils
def main():
train_X, train_Y, test_X, test_Y, classes = utils.load_data_sets()
# 获取数据相关信息
train_num = train_X.shape[0] #训练样本数为209,train_X.shape为(209, 64, 64, 3)
test_num = test_X.shape[0] #测试样本数为50,test_X.shape为(50, 64, 64, 3)
# 本例中num_px=64
px_num = train_X.shape[1] #64
# 转换数据形状
data_dim = px_num * px_num * 3 #64*64*3=12288,即为一个样本(一张图片)的特征维度,即总像素点数量
train_X = train_X.reshape(train_num, data_dim).T #train_X.shape为(12288, 209),即(特征维度,样本大小)
test_X = test_X.reshape(test_num, data_dim).T #test_X.shape为(12288, 50),即(特征维度,样本大小)
# 归一化
train_X = train_X / 255.
test_X = test_X / 255.
# 输入层节点数12288、第一隐藏层节点数20、第二隐藏层节点数7、第三隐藏层节点数5、输出层节点数1
layer = [12288, 20, 7, 5, 1]
parameters = utils.deep_neural_network(train_X, train_Y, layer, 2500)
print 'Train Accuracy:', utils.predict_image(parameters, train_X, train_Y), '%'
print 'Test Accuracy:', utils.predict_image(parameters, test_X, test_Y), '%'
if __name__ == '__main__':
main()

"""
使用paddle框架实现深层神经网络识别猫的问题,关键步骤如下:
1.载入数据和预处理:load_data()
2.定义train()和test()用于读取训练数据和测试数据,分别返回一个reader
3.初始化
4.配置网络结构和设置参数:
- 定义成本函数cost
- 创建parameters
- 定义优化器optimizer
5.定义event_handler
6.定义trainer
7.开始训练
8.预测infer()并输出准确率train_accuracy和test_accuracy
9.展示学习曲线plot_costs()
"""
import matplotlib
#from paddle.v2.plot import Ploter语句引入了PaddlePaddle的绘图工具包,其内部也是调用了matplotlib包。
#在默认设置下,运行绘图代码时可能会遇到“no display name and no$DISPLAY environment variable”的问题。
#这是因为绘图工具函数的默认后端为一些需要图形用户接口(GUI)的后端,而运行的当前环境不满足。
#为此,可加入import matplotlib和matplotlib.use('Agg')语句重新指定不需要GUI的后端,从而解决该问题。
matplotlib.use('Agg')
import matplotlib.pyplot as plt
import numpy as np
import paddle.v2 as paddle
import utils
TRAINING_SET = None
TEST_SET = None
DATA_DIM = None
def load_data():
"""
载入数据,数据项包括:
train_x_ori:原始训练数据集
train_y:原始训练数据标签
test_x_ori:原始测试数据集
test_y:原始测试数据标签
classes(cat/non-cat):分类list
"""
global TRAINING_SET, TEST_SET, DATA_DIM
train_x_ori, train_y, test_x_ori, test_y, classes = utils.load_data_sets()
m_train = train_x_ori.shape[0] #训练样本数为209
m_test = test_x_ori.shape[0] #测试样本数为50
num_px = train_x_ori.shape[1] #64
# 定义纬度,一张图的总像素值即64*64*3,即12288
DATA_DIM = num_px * num_px * 3
# 数据展开,注意此处为了方便处理,没有加上.T的转置操作
train_x_flatten = train_x_ori.reshape(m_train, -1) #(209, 64*64*3)
test_x_flatten = test_x_ori.reshape(m_test, -1) #(50, 64*64*3)
# 归一化
train_x = train_x_flatten / 255.
test_x = test_x_flatten / 255.
TRAINING_SET = np.hstack((train_x, train_y.T))
TEST_SET = np.hstack((test_x, test_y.T))
def read_data(data_set):
"""
读取训练数据或测试数据,服务于train()和test()
Args:
data_set: 要获取的数据集
Return:
reader: 用于获取训练数据集及其标签的生成器generator
"""
def reader():
"""
一个reader
Return:
data[:-1], data[-1:] : 使用yield返回生成器(generator),
data[:-1]表示前n-1个元素,也就是训练数据,data[-1:]表示最后一个元素,也就是对应的标签
"""
for data in data_set:
yield data[:-1], data[-1:]
return reader
def train():
"""
定义一个reader来获取训练数据集及其标签
Return: read_data: 用于获取训练数据集及其标签的reader
"""
global TRAINING_SET
return read_data(TRAINING_SET)
def test():
"""
定义一个reader来获取测试数据集及其标签
Return: read_data: 用于获取测试数据集及其标签的reader
"""
global TEST_SET
return read_data(TEST_SET)
def network_config():
"""
搭建浅层神经网络和配置网络参数
Return:
image: 输入层,DATADIM维稠密向量
y_predict: 输出层,Sigmoid作为激活函数
y_label: 标签数据,1维稠密向量
cost: 损失函数
parameters: 模型参数
optimizer: 优化器
feeding: 数据映射,python字典
"""
# 输入层,paddle.layer.data表示数据层,name=’image’:名称为image,
# type=paddle.data_type.dense_vector(DATA_DIM):数据类型为DATADIM维稠密向量
image = paddle.layer.data(name='image', type=paddle.data_type.dense_vector(DATA_DIM))
# 隐藏层1,paddle.layer.fc表示全连接层,input=image: 该层输入数据为image
# size=20:神经元个数,act=paddle.activation.Relu():激活函数为Relu()
hidden_layer_1 = paddle.layer.fc(input=image, size=20, act=paddle.activation.Relu())
# 隐藏层2,paddle.layer.fc表示全连接层,input=h1: 该层输入数据为h1
# size=7:神经元个数,act=paddle.activation.Relu():激活函数为Relu()
hidden_layer_2 = paddle.layer.fc(input=hidden_layer_1, size=7, act=paddle.activation.Relu())
# 隐藏层3,paddle.layer.fc表示全连接层,input=h2: 该层输入数据为h2
# size=5:神经元个数,act=paddle.activation.Relu():激活函数为Relu()
hidden_layer_3 = paddle.layer.fc(input=hidden_layer_2, size=5, act=paddle.activation.Relu())
# 输出层,paddle.layer.fc表示全连接层,input=h3: 该层输入数据为h3
# size=1:神经元个数,act=paddle.activation.Sigmoid():激活函数为Sigmoid()
y_predict = paddle.layer.fc(input=hidden_layer_3, size=1, act=paddle.activation.Sigmoid())
# 标签数据,paddle.layer.data表示数据层,name=’label’:名称为label
# type=paddle.data_type.dense_vector(1):数据类型为1维稠密向量
y_label = paddle.layer.data(name='label', type=paddle.data_type.dense_vector(1))
# 定义成本函数为交叉熵损失函数multi_binary_label_cross_entropy_cost
cost = paddle.layer.multi_binary_label_cross_entropy_cost(input=y_predict, label=y_label)
# 利用cost创建parameters
parameters = paddle.parameters.create(cost)
# 创建optimizer,并初始化momentum和learning_rate
# 加入动量项Momentum,可以加速更新过程,比如当接近局部最小时,通过震荡作用,跳出局部最小继续下降到全局最小。
# 训练过程在更新权重时采用动量优化器 Momentum ,比如momentum=0.9 代表动量优化每次保持前一次速度的0.9倍。
optimizer = paddle.optimizer.Momentum(momentum=0, learning_rate=0.000075)
# 数据层和数组索引映射,用于trainer训练时喂数据
feeding = {
'image': 0,
'label': 1}
data = [image, y_predict, y_label, cost, parameters, optimizer, feeding]
return data
def get_data(data_creator):
"""
使用参数data_creator来获取测试数据
Args:
data_creator: 数据来源,可以是train()或者test()
Return:
result: 包含测试数据(image)和标签(label)的python字典
"""
data_creator = data_creator
data_image = []
data_label = []
for item in data_creator():
data_image.append((item[0],))
data_label.append(item[1])
result = {
"image": data_image,
"label": data_label
}
return result
def calc_accuracy(probs, data):
"""
根据数据集来计算准确度accuracy
Args:
probs: 数据集的预测结果,调用paddle.infer()来获取
data: 数据集
Return:
calc_accuracy -- 训练准确度
"""
right = 0
total = len(data['label'])
for i in range(len(probs)):
if float(probs[i][0]) > 0.5 and data['label'][i] == 1:
right += 1
elif float(probs[i][0]) < 0.5 and data['label'][i] == 0:
right += 1
accuracy = (float(right) / float(total)) * 100
return accuracy
def infer(y_predict, parameters):
"""
预测并输出模型准确率
Args:
y_predict: 输出层,DATADIM维稠密向量
parameters: 训练完成的模型参数
"""
# 获取测试数据和训练数据,用来验证模型准确度
train_data = get_data(train())
test_data = get_data(test())
# 根据train_data和test_data预测结果,output_layer表示输出层,parameters表示模型参数,input表示输入的测试数据
probs_train = paddle.infer(
output_layer=y_predict,
parameters=parameters,
input=train_data['image']
)
probs_test = paddle.infer(
output_layer=y_predict,
parameters=parameters,
input=test_data['image']
)
# 计算train_accuracy和test_accuracy
print("train_accuracy: {} %".format(calc_accuracy(probs_train, train_data)))
print("test_accuracy: {} %".format(calc_accuracy(probs_test, test_data)))
def plot_costs(costs):
"""
利用costs展示模型的训练曲线
Args: costs: 记录了训练过程的cost变化的list,每一百次迭代记录一次
"""
#确保维度的正确性,可以对矩阵和list进行压缩/降维,比如把list的[[1,2,3]]转换为[1,2,3]
costs = np.squeeze(costs)
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate = 0.000075")
plt.show()
plt.savefig('costs.png')

def main():
"""
定义神经网络结构,训练、预测、检验准确率并打印学习曲线
"""
global DATA_DIM
# 初始化,设置是否使用gpu,trainer数量表示仅使用一个线程进行训练
paddle.init(use_gpu=False, trainer_count=1)
# 载入数据
load_data()
# 配置网络结构和设置参数
image, y_predict, y_label, cost, parameters, optimizer, feeding = network_config()
# 记录成本cost
costs = []
# 处理事件
def event_handler(event):
"""
事件处理器,可以根据训练过程的信息作相应操作
Args: event -- 事件对象,包含event.pass_id, event.batch_id, event.cost等信息
"""
if isinstance(event, paddle.event.EndIteration):
if event.pass_id % 100 == 0:
print("Pass %d, Batch %d, Cost %f" % (event.pass_id, event.batch_id, event.cost))
costs.append(event.cost)
# with open('params_pass_%d.tar' % event.pass_id, 'w') as f:
# parameters.to_tar(f)
# 构造trainer,SGD定义一个随机梯度下降,配置三个参数cost、parameters、update_equation,它们分别表示成本函数、参数和更新公式。
trainer = paddle.trainer.SGD(cost=cost, parameters=parameters, update_equation=optimizer)
"""
模型训练
paddle.reader.shuffle(train(), buf_size=5000):表示trainer从train()这个reader中读取了buf_size=5000大小的数据并打乱顺序
paddle.batch(reader(), batch_size=256):表示从打乱的数据中再取出batch_size=256大小的数据进行一次迭代训练
feeding:用到了之前定义的feeding索引,将数据层image和label输入trainer
event_handler:事件管理机制,可以自定义event_handler,根据事件信息作相应的操作
num_passes:定义训练的迭代次数
"""
trainer.train(
reader=paddle.batch(
paddle.reader.shuffle(train(), buf_size=5000),
batch_size=256),
feeding=feeding,
event_handler=event_handler,
num_passes=3000)
# 预测
infer(y_predict, parameters)
# 展示学习曲线
plot_costs(costs)
if __name__ == '__main__':
main()

Jupyter文件中的内容
Numpy实现深层神经网络
在该实验中我们将介绍如何使用Python及Numpy lib库实现深层神经网络模型来识别猫。本小节代码与第三章Pyhton版本代码大体一致,
区别在于增加了3层隐藏层并设置不同节点数。
图片处理
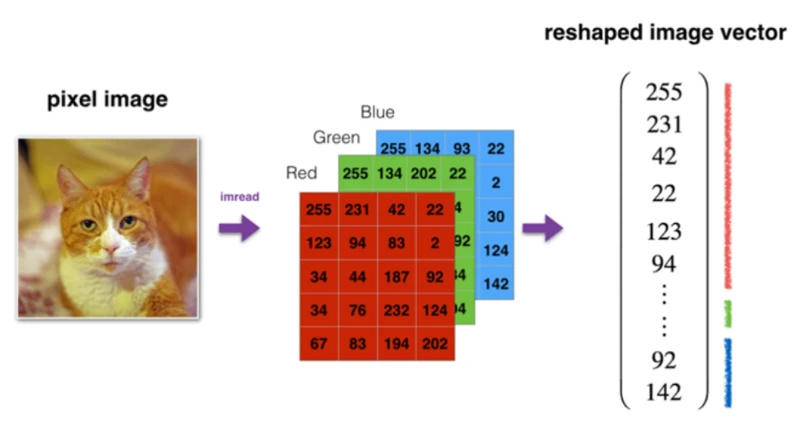
由于识别猫问题涉及到图片处理指示,这里对计算机如何保存图片做一个简单的介绍。在计算机中,图片被存储为三个独立的矩阵,
分别对应图3-6中的红、绿、蓝三个颜色通道,如果图片是64*64像素的,就会有三个64*64大小的矩阵,要把这些像素值放进一个特征向量中,
需要定义一个特征向量X,将三个颜色通道中的所有像素值都列出来。如果图片是64*64大小的,那么特征向量X的总纬度就是64*64*3,也就是12288维。
这样一个12288维矩阵就是Logistic回归模型的一个训练数据。
"""
使用python及numpy库来实现深层神经网络识别猫案例,关键步骤如下:
1.载入数据和预处理:load_data()
2.初始化模型参数(Parameters)
3.循环:
a)计算成本(Cost)
b)计算梯度(Gradient)
c)更新参数(Gradient Descent)
4.利用模型进行预测
5.分析预测结果
6.定义model函数来按顺序将上述步骤合并
"""
import matplotlib
import numpy as np
matplotlib.use('Agg')
import matplotlib.pyplot as plt
import scipy
import h5py
# 定义Sigmoid激活函数
def sigmoid(Z):
"""
使用Sigmoid函数激活
Arguments:
Z -- numpy数组
Returns:
A -- sigmoid(z)的计算值, 与Z维度相同
cache -- 包含Z值,用于后向传播中计算Z的梯度dZ
"""
#前向计算:sigmoid(每层第一步线性映射函数输出的中间值Z) = 每层第二步非线性映射激活函数输出值A
A = 1 / (1 + np.exp(-Z))
#cache即前向计算中每层第一步线性映射函数输出的中间值Z,用于反向传播中计算中间值Z的梯度dZ
cache = Z
return A, cache
# Sigmoid后向传播计算
def sigmoid_backward(dA, cache):
"""
使用Sigmoid函数激活的反向计算
Arguments:
dA -- 激活后的数值的梯度,即每层第二步非线性映射激活函数输出值A的梯度dA
cache -- 包含Z值,即每层第一步线性映射函数输出的中间值Z,用于后向传播中计算Z的梯度dZ
Returns:
dZ -- Z的梯度,即每层第一步线性映射函数输出的中间值Z的梯度dZ
"""
#cache即前向计算中每层第一步线性映射函数输出的中间值Z
Z = cache
#使用前向计算中每层第一步线性映射函数输出的中间值Z来实现:sigmoid(每层第一步线性映射函数输出的中间值Z) = 每层第二步非线性映射激活函数输出值A
#此处sigmoid返回值s也即这一层的第二步非线性映射激活函数输出值A
s = 1 / (1 + np.exp(-Z))
#A的梯度值dA * A * (1 - A) = 第一步线性映射函数输出的中间值Z的梯度dZ
dZ = dA * s * (1 - s)
assert (dZ.shape == Z.shape) #第一步线性映射函数输出的中间值Z 和 其梯度dZ的形状相同
return dZ
# 定义Relu激活函数
def relu(Z):
"""
使用Relu函数激活:A = max(0,Z) 把每层的第一步线性函数输出的中间值Z中小于等于0的值都转换为0返回,大于0则保持不变
Arguments:
Z -- 线性计算的输出值,即每层的第一步线性函数输出的中间值Z
Returns:
A -- Relu激活后的值,维度与Z相同,即每层的第二步非线性函数输出的值A
cache -- 包含Z值,即每层第一步线性映射函数输出的中间值Z,用于后向传播中计算Z的梯度dZ
"""
# Relu激活:A = max(0,Z)的作用把小于等于0的值都转换为0返回,大于0则保持不变
A = np.maximum(0, Z)
assert(A.shape == Z.shape) #第一步线性映射函数输出的中间值Z 和 第二步非线性函数输出的值A的形状相同
#cache即前向计算中每层第一步线性映射函数输出的中间值Z,用于反向传播中计算中间值Z的梯度dZ
cache = Z
return A, cache
#Relu后向传播计算
def relu_backward(dA, cache):
"""
使用Relu函数激活的后向计算
Arguments:
dA -- 激活后的数值的梯度,即每层第二步非线性映射激活函数输出值A的梯度dA
cache -- 包含Z值,即每层第一步线性映射函数输出的中间值Z,用于后向传播中计算Z的梯度dZ
Returns:
dZ -- Z的梯度,即每层第一步线性映射函数输出的中间值Z的梯度dZ
"""
Z = cache
#把第二步非线性函数的输出值a的梯度值da赋值给第一步线性函数输出的中间值z的梯度dz
dZ = np.array(dA, copy=True)
#Z<=0 表示把中间值Z中小于等于0的值转换为True,大于0的值转换为False,最终得出[True ... False]。
#dZ[[True ... False]]=0 表示把dZ中对应索引上为True的值都转换为0,对应索引上为False的值则保持不变,
#即把dZ中小于等于0的值转换为0,大于0的值则保持不变,相当于ReLU函数y=max(0,x)的作用把小于等于0的值都转换为0返回。
#根据“f(第三层隐藏层中间值Z) = max(0,Z) = 第三层隐藏层输出值A”反推导得出第三层隐藏层中间值Z的导数dZ。
dZ[Z <= 0] = 0 # 如果Z<0,则置0即可
assert (dZ.shape == Z.shape) #第一步线性映射函数输出的中间值Z 和 其梯度dZ的形状相同
return dZ
#加载数据
def load_data():
"""
加载数据
"""
train_dataset = h5py.File('datasets/train_catvnoncat.h5', "r")
train_set_x_orig = np.array(train_dataset["train_set_x"][:]) # 训练特征
train_set_y_orig = np.array(train_dataset["train_set_y"][:]) # 训练标签
test_dataset = h5py.File('datasets/test_catvnoncat.h5', "r")
test_set_x_orig = np.array(test_dataset["test_set_x"][:]) # 测试特征
test_set_y_orig = np.array(test_dataset["test_set_y"][:]) # 测试标签
classes = np.array(test_dataset["list_classes"][:]) # class列表
#train_set_y_orig (209,)
#test_set_y_orig (50,)
train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))
test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))
#train_set_x_orig (209, 64, 64, 3)
#train_set_y_orig (1, 209)
#test_set_x_orig (50, 64, 64, 3)
#test_set_y_orig (1, 50)
dataset = [train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes]
return dataset
#初始化参数
def initialize_parameters(n_x, n_h, n_y):
"""
Argument:
n_x -- 输入层节点数
n_h -- 隐藏层节点数
n_y -- 输出层节点数
Returns:
parameters -- 一个字典,包含:
W1 -- 权重矩阵,维度是 (n_h, n_x)
b1 -- 偏移值向量,维度是 (n_h, 1)
W2 -- 权重矩阵,维度是 (n_y, n_h)
b2 -- 偏移值向量,维度是 (n_y, 1)
"""
np.random.seed(1)
W1 = np.random.randn(n_h, n_x)*0.01
b1 = np.zeros((n_h, 1))
W2 = np.random.randn(n_y, n_h)*0.01
b2 = np.zeros((n_y, 1))
assert(W1.shape == (n_h, n_x))
assert(b1.shape == (n_h, 1))
assert(W2.shape == (n_y, n_h))
assert(b2.shape == (n_y, 1))
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
#深层网络的参数初始化
def initialize_parameters_deep(layer_dims):
"""
Arguments:
layer_dims -- 一个list,包含神经网络各层节点数
Returns:
parameters -- 一个字典,包含所有参数: "W1", "b1", ..., "WL", "bL":
Wl -- 权重矩阵,维度是 (layer_dims[l], layer_dims[l-1])
bl -- 偏移值向量,维度是 (layer_dims[l], 1)
"""
np.random.seed(1)
parameters = {}
#传入参数layer_dims= [12288, 20, 7, 5, 1],即[输入层节点数, 隐藏层1节点数, 隐藏层2节点数, 隐藏层3节点数, 输出层节点数]
L = len(layer_dims) # 网络层数为5
"""
第一隐藏层:w1:(20, 12288) b0:(20, 1)
第二隐藏层:w2:(7, 20) b1:(7, 1)
第三隐藏层:w3:(5, 7) b2:(5, 1)
输出层: w4:(1, 5) b3:(1, 1)
"""
#for i in range(1, 4) 所遍历的i值分别为1/2/3/4
for l in range(1, L):
parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l - 1]) / np.sqrt(layer_dims[l - 1])
parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))
assert(parameters['W' + str(l)].shape == (layer_dims[l], layer_dims[l - 1]))
assert(parameters['b' + str(l)].shape == (layer_dims[l], 1))
return parameters
#前向传播的线性计算
def linear_forward(A, W, b):
"""
完成前向传播各层的线性计算
Arguments:
A -- 上一层的输出值,作为本层输入值
W -- 权重矩阵
b -- 偏移值向量
Returns:
Z -- 激活计算的输入
cache -- 一个字典,存储了"A", "W" and "b" 用作后向计算
"""
#前向计算:dot(当前层的权重W,上一层的输出值A)+ 当前层的偏置b = 这一层的第一步线性函数输出的中间值Z
Z = W.dot(A) + b
assert(Z.shape == (W.shape[0], A.shape[1]))
cache = (A, W, b) #cache 包含了前向计算中当前层第一步线性函数所接收的上一层的输出值A、当前层的权重W和偏置b
return Z, cache
#线性计算与激活
def linear_activation_forward(A_prev, W, b, activation):
"""
完成前向传播中各层的线性计算和激活计算
Arguments:
A_prev -- 上一层的输出值,作为本层输入
W -- 权重矩阵
b -- 偏移值向量
activation -- 激活函数选择
Returns:
A -- 激活后的输出值
cache -- 一个字典存储"linear_cache" 和"activation_cache";用作后向传播计算
"""
if activation == "sigmoid":
# 输入: "A_prev, W, b". Outputs: "A, activation_cache".
#前向计算中每层的第一步线性函数:dot(当前层的权重W,上一层的输出值A_prev)+ 当前层的偏置b = 这一层的第一步线性函数输出的中间值Z
Z, linear_cache = linear_forward(A_prev, W, b)
#前向计算中每层的第二步非线性映射激活函数:sigmoid(每层第一步线性映射函数输出的中间值Z) = 每层第二步非线性映射激活函数输出值A
A, activation_cache = sigmoid(Z)
elif activation == "relu":
# 输入: "A_prev, W, b". Outputs: "A, activation_cache".
#前向计算中每层的第一步线性函数:dot(当前层的权重W,上一层的输出值A_prev)+ 当前层的偏置b = 这一层的第一步线性函数输出的中间值Z
Z, linear_cache = linear_forward(A_prev, W, b)
#前向计算中每层的第二步非线性映射激活函数:max(0,第一步线性函数输出的中间值Z) = 第二步非线性映射激活函数输出值A
A, activation_cache = relu(Z)
assert (A.shape == (W.shape[0], A_prev.shape[1]))
#linear_cache 包含了前向计算中当前层第一步线性函数所接收的上一层的输出值A、当前层的权重W和偏置b
#activation_cache 包含了前向计算中每层第一步线性映射函数输出的中间值Z,用于反向传播中计算中间值Z的梯度dZ
cache = (linear_cache, activation_cache)
return A, cache
#L层模型前向传播
def L_model_forward(X, parameters):
"""
完成L层模型的前向传播的计算
Arguments:
X -- 输入值
parameters -- 参数
Returns:
AL -- 模型最终输出
caches -- 包含linear_relu_forward()和linear_sigmoid_forward()的每个cache,每一个cache又包含linear_cache、activation_cache
"""
caches = []
A = X
L = len(parameters) // 2 # 神经网络层数
# L层网络的前向传播计算,即实现L层的隐藏层实现前向计算
for l in range(1, L):
A_prev = A
#L层的隐藏层实现前向计算:计算每层的第一步线性函数+第二步非线性映射激活函数relu 得出模型中每层隐藏层的输出A
A, cache = linear_activation_forward(A_prev, parameters['W' + str(l)], parameters['b' + str(l)], activation="relu")
caches.append(cache)
# 在输出层完成线性计算和激活,即实现输出层第一步线性函数+第二步非线性映射激活函数sigmoid 得出模型最终输出层的输出AL
AL, cache = linear_activation_forward(A, parameters['W' + str(L)], parameters['b' + str(L)], activation="sigmoid")
caches.append(cache)
assert(AL.shape == (1, X.shape[1]))
# 返回模型最终输出预测值AL、cache包含linear_cache和activation_cache
return AL, caches
#计算成本函数
def compute_cost(AL, Y):
"""
完成成本函数计算
Arguments:
AL -- 模型输出值
Y -- 真实值
Returns:
cost -- 成本值
"""
m = Y.shape[1]
# 根据AL和Y计算成本值,此处使用交叉熵损失函数multi_binary_label_cross_entropy_cost
cost = (1. / m) * (-np.dot(Y, np.log(AL).T) - np.dot(1 - Y, np.log(1 - AL).T))
cost = np.squeeze(cost) # To make sure your cost's shape is what we expect (e.g. this turns [[17]] into 17).
assert(cost.shape == ())
return cost
#线性计算的后向传播
def linear_backward(dZ, cache):
"""
完成某一层的后向传播的线性计算部分
Arguments:
dZ -- 线性计算值的梯度
cache -- 包含前向传播的(A_prev, W, b)值
Returns:
dA_prev --前一层输出值的梯度
dW -- 本层权重梯度
db -- 本层偏移值梯度
"""
#前向计算中当前层第一步线性函数所接收的上一层的输出值A_prev、当前层的权重W、当前层的偏置b
A_prev, W, b = cache
m = A_prev.shape[1] #上一层的输出值A_prev的样本数m
#dot(前向计算中第一步线性映射函数输出的中间值Z的梯度dZ, 前向计算中当前层第一步线性函数所接收的上一层的输出值A_prev.T) / m = 当前层权重W的梯度dW
dW = 1. / m * np.dot(dZ, A_prev.T)
#sum(前向计算中第一步线性映射函数输出的中间值Z的梯度dZ) / m = 当前层偏置b的梯度db
db = 1. / m * np.sum(dZ, axis=1, keepdims=True)
#dot(当前层的权重W.T, 前向计算中第一步线性映射函数输出的中间值Z的梯度dZ) = 前向计算中当前层第一步线性函数所接收的上一层输出值A_prev的梯度dA_prev
dA_prev = np.dot(W.T, dZ)
assert (dA_prev.shape == A_prev.shape) #前向计算中当前层第一步线性函数所接收的上一层输出值A_prev和其梯度dA_prev的形状相同
assert (dW.shape == W.shape) #当前层权重W和其梯度dW的形状相同
assert (db.shape == b.shape) #当前层偏置b和其梯度db的形状相同
#返回 前向计算中当前层第一步线性函数所接收的上一层输出值A_prev的梯度dA_prev、当前层权重W的梯度dW、当前层偏置b的梯度db
return dA_prev, dW, db
#线性计算和激活的后向传播计算
def linear_activation_backward(dA, cache, activation):
"""
完成线性计算和激活的后向传播计算
Arguments:
dA -- 本层输出值梯度
cache --包含 (linear_cache, activation_cache)
activation -- 记录激活函数
Returns:
dA_prev -- 上一层输出值的梯度
dW -- 本层权重梯度
db -- 本层偏移值梯度
"""
#linear_cache 包含了前向计算中当前层第一步线性函数所接收的上一层的输出值A、当前层的权重W和偏置b
#activation_cache 包含了前向计算中每层第一步线性映射函数输出的中间值Z,用于反向传播中计算中间值Z的梯度dZ
linear_cache, activation_cache = cache
if activation == "relu":
"""
如果该层的前向计算为第一步线性映射函数+第二步非线性映射激活函数relu的话,那么该层的反向计算顺序如下:
第一步:非线性映射激活函数relu的反向计算
根据 前向计算中第二步非线性映射激活函数输出值A的梯度dA 和 前向计算中第一步线性映射函数输出的中间值Z 计算出 Z的梯度dZ
第二步:线性映射函数的反向计算
根据 前向计算中第一步线性映射函数输出的中间值Z的梯度dZ 和 前向计算中当前层第一步线性函数所接收的上一层输出值A、当前层的权重W和偏置b
计算出 前向计算中当前层第一步线性函数所接收的上一层输出值A的梯度dA_prev、当前层权重W的梯度dW、当前层偏置b的梯度db
"""
dZ = relu_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
elif activation == "sigmoid":
"""
如果该层的前向计算为第一步线性映射函数+第二步非线性映射激活函数sigmoid的话,那么该层的反向计算顺序如下:
第一步:非线性映射激活函数sigmoid的反向计算
根据 前向计算中第二步非线性映射激活函数输出值A的梯度dA 和 前向计算中第一步线性映射函数输出的中间值Z 计算出 Z的梯度dZ
第二步:线性映射函数的反向计算
根据 前向计算中第一步线性映射函数输出的中间值Z的梯度dZ 和 前向计算中当前层第一步线性函数所接收的上一层输出值A、当前层的权重W和偏置b
计算出 前向计算中当前层第一步线性函数所接收的上一层输出值A的梯度dA_prev、当前层权重W的梯度dW、当前层偏置b的梯度db
"""
dZ = sigmoid_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
#返回 前向计算中当前层第一步线性函数所接收的上一层输出值A的梯度dA_prev、当前层权重W的梯度dW、当前层偏置b的梯度db
return dA_prev, dW, db
#L层神经网络模型后向传播
def L_model_backward(AL, Y, caches):
"""
完成L层神经网络模型后向传播计算
Arguments:
AL -- 模型最终输出层的输出值
Y -- 真实值
caches -- 包含Relu和Sigmoid激活函数的linear_activation_forward()中每一个cache,每一个cache又包含linear_cache、activation_cache。
linear_cache 包含了前向计算中当前层第一步线性函数所接收的上一层的输出值A、当前层的权重W和偏置b
activation_cache 包含了前向计算中每层第一步线性映射函数输出的中间值Z,用于反向传播中计算中间值Z的梯度dZ
Returns:
grads -- 包含所有梯度的字典
grads["dA" + str(l)] = ...
grads["dW" + str(l)] = ...
grads["db" + str(l)] = ...
"""
grads = {}
L = len(caches) #模型的层数为4:3层隐藏层+1个输出层
m = AL.shape[1]
Y = Y.reshape(AL.shape) # after this line, Y is the same shape as AL
"""
反向计算:计算模型最终输出层的输出值A的导数 da,用于帮助下一步继续反向计算。
输出值指该层第二步的非线性函数的结果值a,中间值指该层的第一步线性函数的结果值z。
da = - (真实值Y/模型预测值AL) - ((1 - 真实值Y)/(1 - 模型预测值AL))
np.divide(a,b)表示a除以b
"""
# 计算模型最终输出层的输出值A的导数 dAL = - (真实值Y/模型预测值AL) - ((1 - 真实值Y)/(1 - 模型预测值AL))
# 初始化 后向传播计算
dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
# L层神经网络梯度. Inputs: "AL, Y, caches". Outputs: "grads["dAL"], grads["dWL"], grads["dbL"]
# caches[3] 为取出的最后一层输出层的linear_cache、activation_cache
current_cache = caches[L - 1]
# 传入 模型输出层的输出值A的导数 dAL、current_cache所包含的输出层的linear_cache、activation_cache,
# 计算出 前向计算中当前输出层第一步线性函数所接收的上一层隐藏层输出值A的梯度dA_prev、当前输出层权重W的梯度dW、当前输出层偏置b的梯度db
# 存储到字典中的分别是 grads["dA4"], grads["dW4"], grads["db4"]
grads["dA" + str(L)], grads["dW" + str(L)], grads["db" + str(L)] = linear_activation_backward(dAL, current_cache, activation="sigmoid")
# 计算 前向计算中每层隐藏层第一步线性函数所接收的上一层隐藏层输出值A的梯度dA_prev、每层隐藏层权重W的梯度dW、每层隐藏层偏置b的梯度db
# for i in reversed(range(3)) 遍历出的i值分别为 2/1/0
for l in reversed(range(L - 1)):
# 第L层: (RELU -> LINEAR) 梯度
# 获取 前向计算中每层隐藏层的linear_cache、activation_cache
# linear_cache 包含了前向计算中当前隐藏层第一步线性函数所接收的上一层隐藏层的输出值A、当前隐藏层的权重W和偏置b
# activation_cache 包含了前向计算中每层隐藏层第一步线性映射函数输出的中间值Z,用于反向传播中计算中间值Z的梯度dZ
#caches[2]/caches[1]/caches[0] 表示分别获取的是第三隐藏层、第二隐藏层、第一隐藏层的linear_cache、activation_cache
current_cache = caches[l]
#每次分别传入的是grads["dA4"]/grads["dA3"]/grads["dA2"]
#grads["dA4"]:前向计算中输出层第一步线性函数所接收的上一层第三隐藏层输出值A的梯度dA_prev
#grads["dA3"]:前向计算中第三隐藏层第一步线性函数所接收的上一层第二隐藏层输出值A的梯度dA_prev
#grads["dA2"]:前向计算中第二隐藏层第一步线性函数所接收的上一层第一隐藏层输出值A的梯度dA_prev
dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA" + str(l + 2)], current_cache, activation="relu")
grads["dA" + str(l + 1)] = dA_prev_temp #存储到字典中的分别是 grads["dA3"]、grads["dA2"]、grads["dA1"]
grads["dW" + str(l + 1)] = dW_temp #存储到字典中的分别是 grads["dW3"]、 grads["dW2"]、 grads["dW1"]
grads["db" + str(l + 1)] = db_temp #存储到字典中的分别是 grads["db3"]、grads["db2"]、grads["db1"]
"""
grads["dW4"]、grads["dW3"]、grads["dW2"]、 grads["dW1"]:分别表示输出层/第三隐藏层/第二隐藏层/第一隐藏层 权重W的梯度dW
grads["db4"]、grads["db3"]、grads["db2"]、grads["db1"]:分别表示输出层/第三隐藏层/第二隐藏层/第一隐藏层 偏置b的梯度db
grads["dA4"]、grads["dA3"]、grads["dA2"]、grads["dA1"]:
grads["dA4"]:前向计算中输出层第一步线性函数所接收的上一层第三隐藏层输出值A的梯度dA_prev
grads["dA3"]:前向计算中第三隐藏层第一步线性函数所接收的上一层第二隐藏层输出值A的梯度dA_prev
grads["dA2"]:前向计算中第二隐藏层第一步线性函数所接收的上一层第一隐藏层输出值A的梯度dA_prev
grads["dA1"]:前向计算中第一隐藏层第一步线性函数所接收的上一层输出值x的梯度dA_prev
"""
return grads
#参数更新
def update_parameters(parameters, grads, learning_rate):
"""
#根据梯度完成参数更新
Arguments:
parameters -- 包含所有参数的字典
grads -- 包含梯度的字典
Returns:
parameters -- 一个字典,包含所有更新后的参数
parameters["W" + str(l)] = ...
parameters["b" + str(l)] = ...
"""
# number of layers in the neural network
L = len(parameters) // 2 #L为4
"""
第一隐藏层:w1:(20, 12288) b0:(20, 1)
第二隐藏层:w2:(7, 20) b1:(7, 1)
第三隐藏层:w3:(5, 7) b2:(5, 1)
输出层: w4:(1, 5) b3:(1, 1)
"""
# 使用循环更新每个参数
# for i in range(4) 所遍历的i分别为0/1/2/3
for l in range(L):
"""
parameters["W1"] = parameters["W1"] - learning_rate * grads["dW1"]
parameters["W2"] = parameters["W2"] - learning_rate * grads["dW2"]
parameters["W3"] = parameters["W3"] - learning_rate * grads["dW3"]
parameters["W4"] = parameters["W4"] - learning_rate * grads["dW4"]
"""
parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * grads["dW" + str(l + 1)]
parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * grads["db" + str(l + 1)]
return parameters
#预测
def predict(X, y, parameters):
"""
用训练后的L层模型预测结果
Arguments:
X -- 输入值
y --真实标签集
parameters -- 训练后的参数
Returns:
p -- 对输入值X的预测
"""
m = X.shape[1] #样本数
n = len(parameters) // 2 # 4
p = np.zeros((1, m)) #存储0/1结果的预测标签集
# 前向传播计算
# 返回模型最终输出预测概率值probas、caches包含linear_cache和activation_cache
probas, caches = L_model_forward(X, parameters)
# 将预测值转换为0/1,即将预测概率值大于0.5的赋值为1,反之赋值为0
for i in range(0, probas.shape[1]):
if probas[0, i] > 0.5:
p[0, i] = 1
else:
p[0, i] = 0
# 打印结果
# print ("predictions: " + str(p))
# print ("true labels: " + str(y))
#sum(p == y) 表示把预测标签集p和真实标签集中的每个对应索引上的值进行对比,相同返回1,然后计算总和再除以样本数,得出准确率
print(str(float(np.sum(p == y)) / float(m)))
return p
#打印未识别的图片
def print_mislabeled_images(classes, X, y, p):
"""
画出未识别的图片
X -- 数据
y -- 真实值
p -- 预测值
"""
a = p + y
mislabeled_indices = np.asarray(np.where(a == 1))
plt.rcParams['figure.figsize'] = (40.0, 40.0) # set default size of plots
num_images = len(mislabeled_indices[0])
for i in range(num_images):
index = mislabeled_indices[1][i]
plt.subplot(2, num_images, i + 1)
plt.imshow(X[:, index].reshape(64, 64, 3), interpolation='nearest')
plt.axis('off')
plt.title("Prediction: " + classes[int(p[0, index])]
.decode("utf-8") + " \n Class: " + classes[y[0, index]].decode("utf-8"))
"""
train_set_x_orig (209, 64, 64, 3)
train_set_y_orig (1, 209)
test_set_x_orig (50, 64, 64, 3)
test_set_y_orig (1, 50)
"""
#加载数据
train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = load_data()
m_train = train_set_x_orig.shape[0] #训练样本数为209
m_test = test_set_x_orig.shape[0] #测试样本数为50
num_px = train_set_x_orig.shape[1] #64
#reshape(m_train, -1)即为(209, 64*64*3),然后转置为(12288, 209),即(特征维度,样本大小)
train_set_x_flatten = train_set_x_orig.reshape(m_train, -1).T
#reshape(m_test, -1)即为(50, 64*64*3),(12288, 50),即(特征维度,样本大小)
test_set_x_flatten = test_set_x_orig.reshape(m_test, -1).T
# 归一化
train_set_x = train_set_x_flatten / 255.
test_set_x = test_set_x_flatten / 255.
# L层神经网络模型
def L_layer_model(X, Y, layers_dims, learning_rate=0.0075, num_iterations=3000, print_cost=False):
"""
完成L层神经网络模型(包含前向以及后向传播)
Arguments:
X -- 输入值
Y -- 真实值
layers_dims -- 存有各层节点数的list
learning_rate -- 学习率
num_iterations -- 训练次数
print_cost -- 如果为真,每100次打印一次cost值
Returns:
parameters -- 训练后的参数
"""
np.random.seed(1)
costs = [] # keep track of cost
# 初始化参数
parameters = initialize_parameters_deep(layers_dims)
# 训练
for i in range(0, num_iterations):
# 前向传播计算
# 返回模型最终输出预测概率值AL、caches包含linear_cache和activation_cache
AL, caches = L_model_forward(X, parameters)
# 计算成本
cost = compute_cost(AL, Y)
# 后向传播
grads = L_model_backward(AL, Y, caches)
# 更新参数
parameters = update_parameters(parameters, grads, learning_rate)
# 每100次训练打印cost
if print_cost and i % 100 == 0:
print ("Cost after iteration %i: %f" % (i, cost))
if print_cost and i % 100 == 0:
costs.append(cost)
# 绘制cost
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
plt.savefig("costs.png")
return parameters
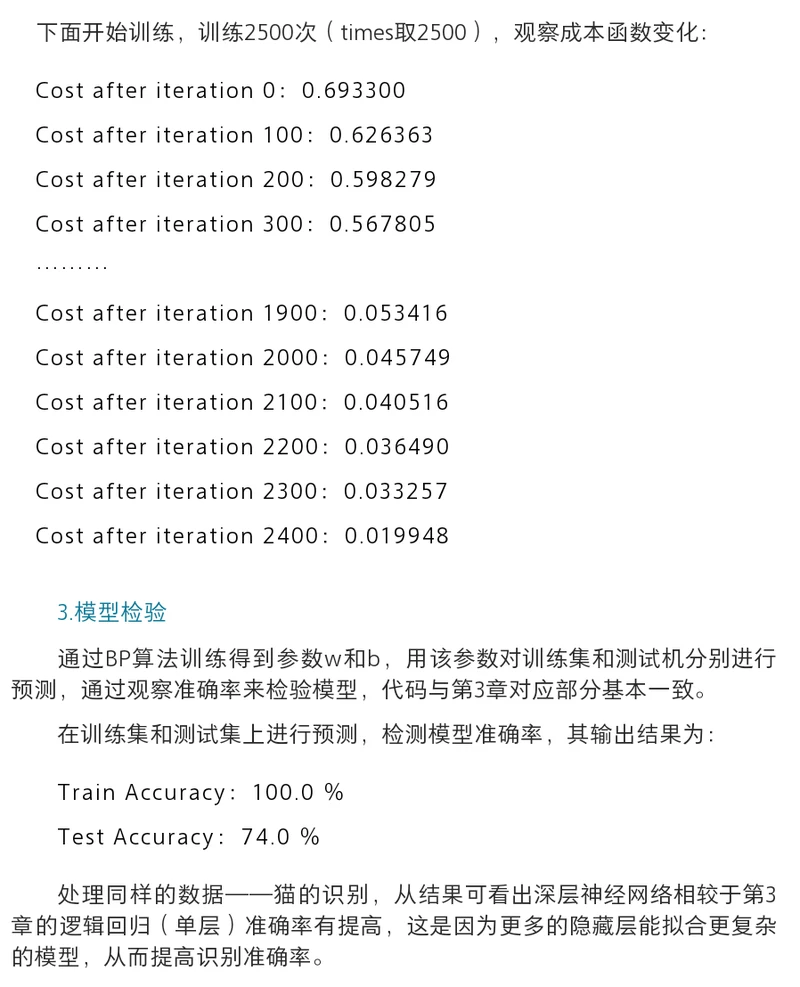
下面开始训练,训练2500次,观察成本函数变化
#设置神经网络规模,5个数字分别表示从输入层到隐藏层到输出层各层节点数
layers_dims = [12288, 20, 7, 5, 1]
parameters = dnn_app_utils_v2.L_layer_model(train_x, train_y, layers_dims, num_iterations = 2500, print_cost = True)
"""
用于载入数据,目标数据源为两个.h5文件,分别为:
train_catvnoncat.h5:训练数据集(猫图片)
test_catvnoncat.h5:测试数据集(猫图片)
"""
import numpy as np
import h5py
def load_dataset():
"""
用于从两个.h5文件中分别加载训练数据和测试数据
Return:
train_set_x_orig -- 原始训练数据集
train_set_y -- 原始训练数据标签
test_set_x_orig -- 原始测试数据集
test_set_y -- 原始测试数据标签
classes(cat/non-cat) -- 分类list
"""
train_dataset = h5py.File('datasets/train_catvnoncat.h5', "r")
train_set_x_orig = np.array(train_dataset["train_set_x"][:]) # your train set features
train_set_y_orig = np.array(train_dataset["train_set_y"][:]) # your train set labels
test_dataset = h5py.File('datasets/test_catvnoncat.h5', "r")
test_set_x_orig = np.array(test_dataset["test_set_x"][:]) # your test set features
test_set_y_orig = np.array(test_dataset["test_set_y"][:]) # your test set labels
classes = np.array(test_dataset["list_classes"][:]) # the list of classes
train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))
test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))
dataset = [train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes]
return dataset
1.引用库
首先,载入几个需要用到的库,它们分别是:
numpy:一个python的基本库,用于科学计算
matplotlib.pyplot:用于生成图,在验证模型准确率和展示成本变化趋势时会使用到
h5py:用于处理hdf5文件数据
dnn_app_utils_v2:包含了一些有用的工具函数
import numpy as np
import matplotlib.pyplot as plt
import h5py
import dnn_app_utils_v2
2.数据预处理
这里简单介绍数据集及其结构。数据集以hdf5文件的形式存储,包含了如下内容:
训练数据集:包含了m_train个图片的数据集,数据的标签(Label)分为cat(y=1)和non-cat(y=0)两类。
测试数据集:包含了m_test个图片的数据集,数据的标签(Label)同上。
单个图片数据的存储形式为(num_x, num_x, 3),其中num_x表示图片的长或宽(数据集图片的长和宽相同),数字3表示图片的三通道(RGB)。
在代码中使用一行代码来读取数据,读者暂不需要了解数据的读取过程,只需调用load_dataset()方法,并存储五个返回值,以便后续的使用。
train_x_orig, train_y, test_x_orig, test_y, classes = dnn_app_utils_v2.load_data()
#数据预处理
train_x_flatten = train_x_orig.reshape(train_x_orig.shape[0], -1).T # The "-1" makes reshape flatten the remaining dimensions
test_x_flatten = test_x_orig.reshape(test_x_orig.shape[0], -1).T
#归一化
train_x = train_x_flatten/255.
test_x = test_x_flatten/255.
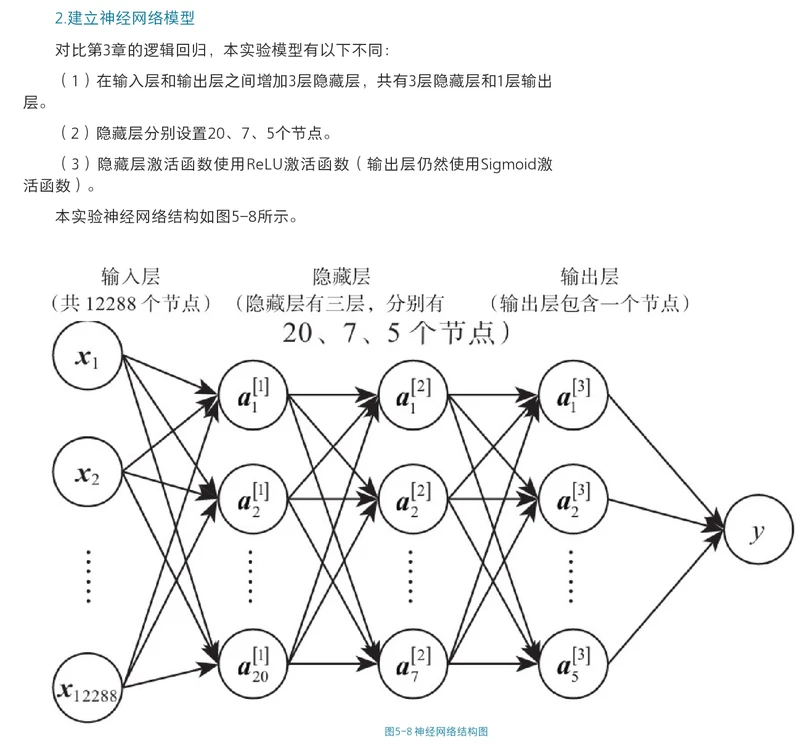
3.建立神经网络模型
对比“浅层神经网络”的网络结构,本小节神经网络模型有以下不同:
增加2层隐藏层,共有3层隐藏层和1层输出层;
第一层设置20个节点,第二层7个,第三层5个;
隐藏层激活函数使用Relu激活函数。
在dnn_app_utils_v2文件中已包含下列函数,在实现神经网络模型中将直接调用(下列函数在第四章Python代码部分均有实现,
根据网络结构不同略有差异):
初始化参数 initialize_parameters_deep(layer_dims)
正向传播 L_model_forward(X, parameters)
成本函数 compute_cost(AL, Y)
反向传播 L_model_backward(AL, Y, caches)
参数更新 update_parameters(parameters, grads, learning_rate)
#设置神经网络规模,5个数字分别表示从输入层到隐藏层到输出层各层节点数
layers_dims = [12288, 20, 7, 5, 1]
#定义函数:L层神经网络模型
def L_layer_model(X, Y, layers_dims, learning_rate = 0.0075, num_iterations = 3000, print_cost=False):
"""
L层神经网络正向传播: [加权偏移->RELU激活]*(L-1)->加权激活->SIGMOID激活.
参数:
X -- 输入值,维度为 (样本个数, 像素num_px * num_px * 3)
Y -- 真实值(0表示不是猫,1表示是猫),维度为 (1, 样本个数)
layers_dims -- 各层节点数
learning_rate -- 学习率
num_iterations -- 训练次数
print_cost -- 参数设置True,则每100次训练打印一次成本函数值
返回值:
parameters -- 模型训练所得参数,用于预测
"""
np.random.seed(1)
costs = []
#参数初始化
parameters = dnn_app_utils_v2.initialize_parameters_deep(layers_dims)
#训练
for i in range(0, num_iterations):
#正向传播: [加权偏移 -> RELU激活]*(L-1) -> 加权偏移后 -> SIGMOID激活
AL, caches = dnn_app_utils_v2.L_model_forward(X, parameters)
#计算成本函数
cost = dnn_app_utils_v2.compute_cost(AL, Y)
#反向传播
grads = dnn_app_utils_v2.L_model_backward(AL, Y, caches)
#更新参数
parameters = dnn_app_utils_v2.update_parameters(parameters, grads, learning_rate)
#每100次训练打印一次成本函数
if print_cost and i % 100 == 0:
print ("Cost after iteration %i: %f" %(i, cost))
if print_cost and i % 100 == 0:
costs.append(cost)
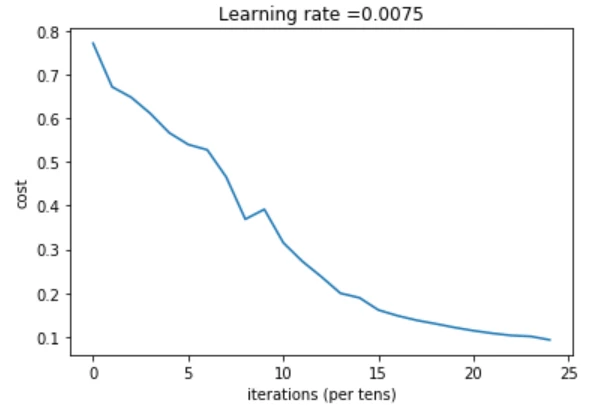
#绘制损失函数变化折线图
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters
下面开始训练,训练2500次,观察成本函数变化
parameters = dnn_app_utils_v2.L_layer_model(train_x, train_y, layers_dims, num_iterations = 2500, print_cost = True)
Cost after iteration 0: 0.771749
Cost after iteration 100: 0.672053
Cost after iteration 200: 0.648263
Cost after iteration 300: 0.611507
Cost after iteration 400: 0.567047
Cost after iteration 500: 0.540138
Cost after iteration 600: 0.527930
Cost after iteration 700: 0.465477
Cost after iteration 800: 0.369126
Cost after iteration 900: 0.391747
Cost after iteration 1000: 0.315187
Cost after iteration 1100: 0.272700
Cost after iteration 1200: 0.237419
Cost after iteration 1300: 0.199601
Cost after iteration 1400: 0.189263
Cost after iteration 1500: 0.161189
Cost after iteration 1600: 0.148214
Cost after iteration 1700: 0.137775
Cost after iteration 1800: 0.129740
Cost after iteration 1900: 0.121225
Cost after iteration 2000: 0.113821
Cost after iteration 2100: 0.107839
Cost after iteration 2200: 0.102855
Cost after iteration 2300: 0.100897
Cost after iteration 2400: 0.092878
4.在训练集和测试集上进行预测,检测模型准确率,训练集和测试集准确率分别为0.986和0.8:
print(‘Train Accuracy’)
pred_train = predict(train_x, train_y, parameters)
print(‘Test Accuracy’)
pred_test = predict(test_x, test_y, parameters)
从准确率看,相比于第三章的逻辑回归(本章节处理的数据与第三章相同),深层神经网络准确率提高了不少,这是因为深层神经网络提供更多隐藏层,
使得神经网络能够拟合更复杂的模型,识别图片准确率更高。
Paddlepaddle实现浅层神经网络回归
在该实验中,我们将使用PaddlePaddle实现深层神经网络,解决识别猫的问题,使用的数据与“Paddlepaddle实现Logistic回归”中一致。
该版本代码与第三章PaddlePaddle部分代码大体一致,区别在于增加了隐藏层并设置不同隐藏层节点,隐藏层激活函数换为Relu激活函数,同时修改训练次数和学习率。
1.引用库
首先,载入几个需要用到的库,它们分别是:
numpy:一个python的基本库,用于科学计算
dnn_utils:定义了一些工具函数
paddle.v2:paddle深度学习平台
matplotlib.pyplot:用于生成图,在验证模型准确率和展示成本变化趋势时会使用到
import matplotlib
import numpy as np
import paddle.v2 as paddle
import matplotlib.pyplot as plt
import dnn_utils
TRAINING_SET = None
TEST_SET = None
DATADIM = None
2.数据预处理
数据与“Paddlepaddle实现浅层神经网络”中一致,包含了如下内容:
训练数据集:包含了m_train个图片的数据集,数据的标签(Label)分为cat(y=1)和non-cat(y=0)两类。
测试数据集:包含了m_test个图片的数据集,数据的标签(Label)同上。
# 载入数据(cat/non-cat)
def load_data():
"""
载入数据,数据项包括:
train_set_x_orig:原始训练数据集
train_set_y:原始训练数据标签
test_set_x_orig:原始测试数据集
test_set_y:原始测试数据标签
classes(cat/non-cat):分类list
"""
global TRAINING_SET, TEST_SET, DATADIM
train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = dnn_utils.load_dataset()
m_train = train_set_x_orig.shape[0]
m_test = test_set_x_orig.shape[0]
num_px = train_set_x_orig.shape[1]
# 定义纬度
DATADIM = num_px * num_px * 3
# 数据展开,注意此处为了方便处理,没有加上.T的转置操作
train_set_x_flatten = train_set_x_orig.reshape(m_train, -1)
test_set_x_flatten = test_set_x_orig.reshape(m_test, -1)
# 归一化
train_set_x = train_set_x_flatten / 255.
test_set_x = test_set_x_flatten / 255.
TRAINING_SET = np.hstack((train_set_x, train_set_y.T))
TEST_SET = np.hstack((test_set_x, test_set_y.T))
3.构造reader
构造两个reader()函数来分别读取训练数据集TRAINING_SET和测试数据集TEST_SET,需要注意的是,yield关键字的作用类似return关键字,
但不同指出在于yield关键字让reader()变成一个生成器(Generator),生成器不会创建完整的数据集列表,而是在每次循环时计算下一个值,
这样不仅节省内存空间,而且符合reader的定义,也即一个真正的读取器。
# 读取训练数据或测试数据,服务于train()和test()
def read_data(data_set):
"""
一个reader
Args: data_set -- 要获取的数据集
Return: reader -- 用于获取训练数据集及其标签的生成器generator
"""
def reader():
"""
一个reader
Return:
data[:-1], data[-1:] -- 使用yield返回生成器(generator),
data[:-1]表示前n-1个元素,也就是训练数据,data[-1:]表示最后一个元素,也就是对应的标签
"""
for data in data_set:
yield data[:-1], data[-1:]
return reader
# 获取训练数据集
def train():
"""
定义一个reader来获取训练数据集及其标签
Return: read_data -- 用于获取训练数据集及其标签的reader
"""
global TRAINING_SET
return read_data(TRAINING_SET)
# 获取测试数据集
def test():
"""
定义一个reader来获取测试数据集及其标签
Return: read_data -- 用于获取测试数据集及其标签的reader
"""
global TEST_SET
return read_data(TEST_SET)
4.配置网络结构和设置参数
开始配置网络结构,这是本章与Logistic回归的不同之处,本章节实现双层神经网络,增加了一层隐藏层,隐藏层设置7个节点,激活函数使用Relu,其余不变。
1.损失函数
在这里使用PaddlePaddle提供的交叉熵损失函数,cost = paddle.layer.multi_binary_label_cross_entropy_cost(input=y_predict, label=y_label)
定义了成本函数,并使用y_predict与label计算成本。定义了成本函数之后,使用PaddlePaddle提供的简单接口
parameters=paddle.parameters.create(cost)来创建和初始化参数。
2.optimizer
参数创建完成后,定义参数优化器optimizer= paddle.optimizer.Momentum(momentum=0, learning_rate=0.000075),
使用Momentum作为优化器,并设置动量momentum为零,学习率为0.00002。注意,读者暂时无需了解Momentum的含义,只需要学会使用即可。
3.其它配置
feeding={‘image’:0, ‘label’:1}是数据层名称和数组索引的映射,用于在训练时输入数据。
# 配置网络结构和设置参数
def netconfig():
"""
配置网络结构和设置参数
Return:
image -- 输入层,DATADIM维稠密向量
y_predict -- 输出层,Sigmoid作为激活函数
y_label -- 标签数据,1维稠密向量
cost -- 损失函数
parameters -- 模型参数
optimizer -- 优化器
feeding -- 数据映射,python字典
"""
# 输入层,paddle.layer.data表示数据层,name=’image’:名称为image,
# type=paddle.data_type.dense_vector(DATADIM):数据类型为DATADIM维稠密向量
image = paddle.layer.data(name='image', type=paddle.data_type.dense_vector(DATADIM))
# 隐藏层1,paddle.layer.fc表示全连接层,input=image: 该层输入数据为image
# size=20:神经元个数,act=paddle.activation.Relu():激活函数为Relu()
h1 = paddle.layer.fc(input=image, size=20, act=paddle.activation.Relu())
# 隐藏层2,paddle.layer.fc表示全连接层,input=h1: 该层输入数据为h1
# size=7:神经元个数,act=paddle.activation.Relu():激活函数为Relu()
h2 = paddle.layer.fc(input=h1, size=7, act=paddle.activation.Relu())
# 隐藏层3,paddle.layer.fc表示全连接层,input=h2: 该层输入数据为h2
# size=5:神经元个数,act=paddle.activation.Relu():激活函数为Relu()
h3 = paddle.layer.fc(input=h2, size=5, act=paddle.activation.Relu())
# 输出层,paddle.layer.fc表示全连接层,input=h3: 该层输入数据为h3
# size=1:神经元个数,act=paddle.activation.Sigmoid():激活函数为Sigmoid()
y_predict = paddle.layer.fc(input=h3, size=1, act=paddle.activation.Sigmoid())
# 标签数据,paddle.layer.data表示数据层,name=’label’:名称为label
# type=paddle.data_type.dense_vector(1):数据类型为1维稠密向量
y_label = paddle.layer.data(name='label', type=paddle.data_type.dense_vector(1))
# 定义成本函数为交叉熵损失函数multi_binary_label_cross_entropy_cost
cost = paddle.layer.multi_binary_label_cross_entropy_cost(input=y_predict, label=y_label)
# 利用cost创建parameters
parameters = paddle.parameters.create(cost)
# 创建optimizer,并初始化momentum和learning_rate
# 加入动量项Momentum,可以加速更新过程,比如当接近局部最小时,通过震荡作用,跳出局部最小继续下降到全局最小。
# 训练过程在更新权重时采用动量优化器 Momentum ,比如momentum=0.9 代表动量优化每次保持前一次速度的0.9倍。
optimizer = paddle.optimizer.Momentum(momentum=0, learning_rate=0.000075)
# 数据层和数组索引映射,用于trainer训练时喂数据
feeding = {
'image': 0,
'label': 1}
data = [image, y_predict, y_label, cost, parameters, optimizer, feeding]
return data
5.训练过程
接下来进入训练过程。
1.初始化
首先进行最基本的初始化操作,paddle.init(use_gpu=False, trainer_count=1) 表示不使用gpu进行训练并且仅使用一个trainer进行训练,
load_data()用于获取并预处理数据
# 初始化,trainer数量表示仅使用一个线程进行训练
paddle.init(use_gpu=False, trainer_count=1)
# 获取数据并预处理
load_data()
# 配置网络结构和设置参数
image, y_predict, y_label, cost, parameters, optimizer, feeding = netconfig()
# 记录成本cost
costs = []
2.模型训练
上述内容进行了初始化并配置了网络结构,接下来利用上述配置进行模型训练。
首先定义一个随机梯度下降trainer,配置三个参数cost、parameters、update_equation,它们分别表示成本函数、参数和更新公式。
再利用trainer.train()即可开始真正的模型训练:
paddle.reader.shuffle(train(), buf_size=5000)表示trainer从train()这个reader中读取了buf_size=5000大小的数据并打乱顺序
paddle.batch(reader(), batch_size=256)表示从打乱的数据中再取出batch_size=256大小的数据进行一次迭代训练
参数feeding用到了之前定义的feeding索引,将数据层image和label输入trainer,也就是训练数据的来源。
参数event_handler是事件管理机制,读者可以自定义event_handler,根据事件信息作相应的操作。
参数num_passes=5000表示迭代训练5000次后停止训练。
def event_handler(event):
"""
事件处理器,可以根据训练过程的信息作相应操作
Args: event -- 事件对象,包含event.pass_id, event.batch_id, event.cost等信息
"""
if isinstance(event, paddle.event.EndIteration):
if event.pass_id % 100 == 0:
print("Pass %d, Batch %d, Cost %f" % (event.pass_id, event.batch_id, event.cost))
costs.append(event.cost)
with open('params_pass_%d.tar' % event.pass_id, 'w') as f:
parameters.to_tar(f)
# 构造trainer,SGD定义一个随机梯度下降,配置三个参数cost、parameters、update_equation,
# 它们分别表示成本函数、参数和更新公式。
trainer = paddle.trainer.SGD(cost=cost, parameters=parameters, update_equation=optimizer)
"""
模型训练
paddle.reader.shuffle(train(), buf_size=5000):表示trainer从train()这个reader中读取了buf_size=5000大小的数据并打乱顺序
paddle.batch(reader(), batch_size=256):表示从打乱的数据中再取出batch_size=256大小的数据进行一次迭代训练
feeding:用到了之前定义的feeding索引,将数据层image和label输入trainer
event_handler:事件管理机制,可以自定义event_handler,根据事件信息作相应的操作
num_passes:定义训练的迭代次数
"""
trainer.train(
reader=paddle.batch(
paddle.reader.shuffle(train(), buf_size=5000),
batch_size=256),
feeding=feeding,
event_handler=event_handler,
num_passes=3000)
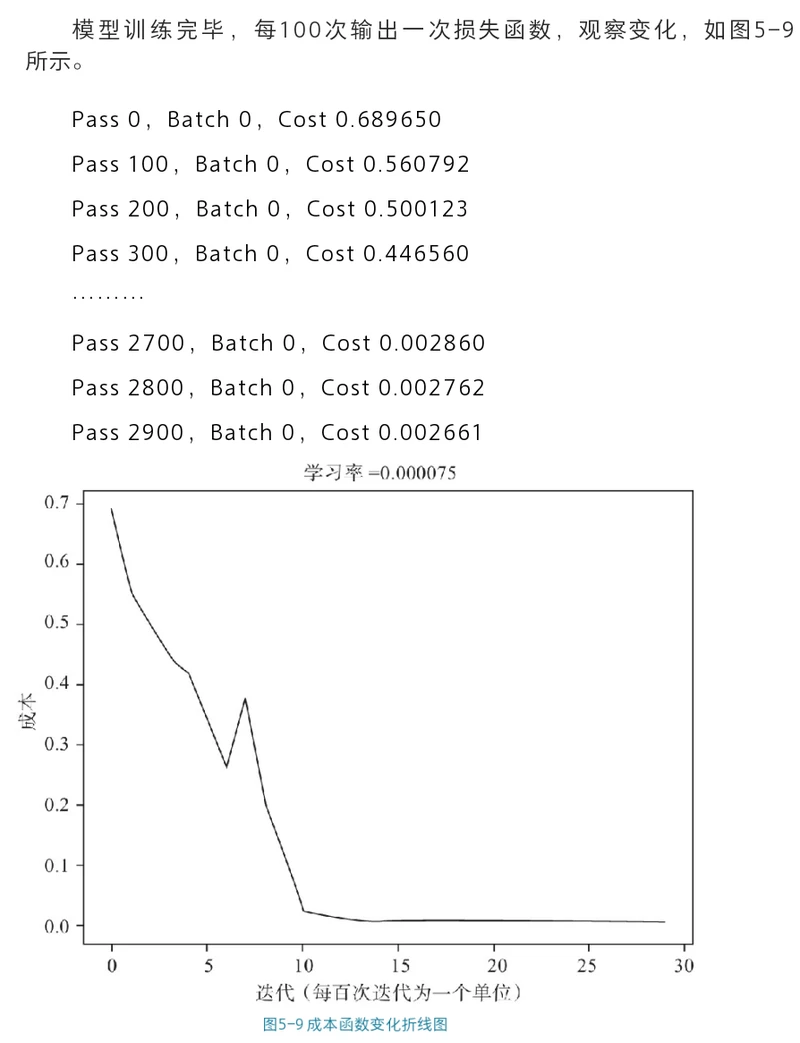
Pass 0, Batch 0, Cost 0.689650
Pass 100, Batch 0, Cost 0.560792
Pass 200, Batch 0, Cost 0.500123
Pass 300, Batch 0, Cost 0.446560
Pass 400, Batch 0, Cost 0.423323
Pass 500, Batch 0, Cost 0.340073
Pass 600, Batch 0, Cost 0.264567
Pass 700, Batch 0, Cost 0.378781
Pass 800, Batch 0, Cost 0.200616
Pass 900, Batch 0, Cost 0.127956
Pass 1000, Batch 0, Cost 0.022886
Pass 1100, Batch 0, Cost 0.014010
Pass 1200, Batch 0, Cost 0.010211
Pass 1300, Batch 0, Cost 0.008157
Pass 1400, Batch 0, Cost 0.006822
Pass 1500, Batch 0, Cost 0.005900
Pass 1600, Batch 0, Cost 0.005245
Pass 1700, Batch 0, Cost 0.004771
Pass 1800, Batch 0, Cost 0.004403
Pass 1900, Batch 0, Cost 0.004099
Pass 2000, Batch 0, Cost 0.003858
Pass 2100, Batch 0, Cost 0.003668
Pass 2200, Batch 0, Cost 0.003501
Pass 2300, Batch 0, Cost 0.003354
Pass 2400, Batch 0, Cost 0.003217
Pass 2500, Batch 0, Cost 0.003094
Pass 2600, Batch 0, Cost 0.002978
Pass 2700, Batch 0, Cost 0.002870
Pass 2800, Batch 0, Cost 0.002766
Pass 2900, Batch 0, Cost 0.002668
3.模型检验
1.模型训练完成后,接下来检验模型的准确率。
首先定义get_data()函数来帮助我们读取训练数据和测试数据。
# 获取data
def get_data(data_creator):
"""
使用参数data_creator来获取测试数据
Args: data_creator -- 数据来源,可以是train()或者test()
Return: result -- 包含测试数据(image)和标签(label)的python字典
"""
data_creator = data_creator
data_image = []
data_label = []
for item in data_creator():
data_image.append((item[0],))
data_label.append(item[1])
result = {
"image": data_image,
"label": data_label
}
return result
2.获得数据之后,我们就可以开始利用paddle.infer()来进行预测,参数output_layer 表示输出层,参数parameters表示模型参数,
参数input表示输入的测试数据。
# 获取测试数据和训练数据,用来验证模型准确度
train_data = get_data(train())
test_data = get_data(test())
# 根据train_data和test_data预测结果,output_layer表示输出层,parameters表示模型参数,input表示输入的测试数据
probs_train = paddle.infer(output_layer=y_predict, parameters=parameters, input=train_data['image'])
probs_test = paddle.infer(output_layer=y_predict, parameters=parameters, input=test_data['image'])
3.获得检测结果probs_train和probs_test之后,我们将结果转化为二分类结果并计算预测正确的结果数量,
定义calc_accuracy()来分别计算训练准确度和测试准确度。
# 计算准确度
def calc_accuracy(probs, data):
"""
根据数据集来计算准确度accuracy
Args:
probs -- 数据集的预测结果,调用paddle.infer()来获取
data -- 数据集
Return:
calc_accuracy -- 训练准确度
"""
right = 0
total = len(data['label'])
for i in range(len(probs)):
if float(probs[i][0]) > 0.5 and data['label'][i] == 1:
right += 1
elif float(probs[i][0]) < 0.5 and data['label'][i] == 0:
right += 1
accuracy = (float(right) / float(total)) * 100
return accuracy
4.调用上述两个函数并输出
# 计算train_accuracy和test_accuracy
print("train_accuracy: {} %".format(calc_accuracy(probs_train, train_data)))
print("test_accuracy: {} %".format(calc_accuracy(probs_test, test_data)))
#train_accuracy: 100.0 %
#test_accuracy: 80.0 %
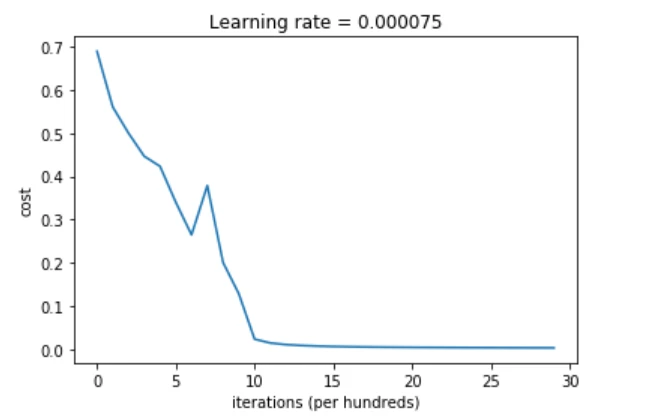
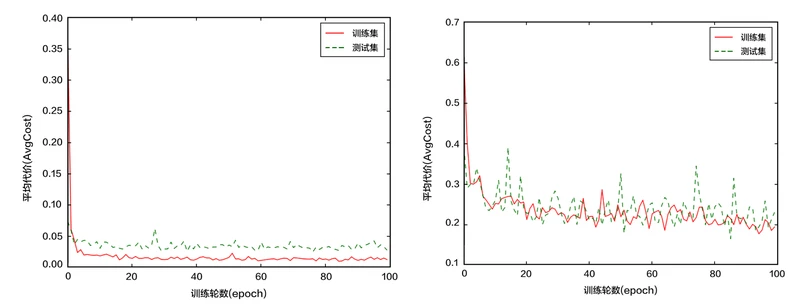
5.学习曲线
可以输出成本的变化情况,利用学习曲线对模型进行分析。
读者可以看到图中成本在刚开始收敛较快,随着迭代次数变多,收敛速度变慢,最终收敛到一个较小值。
#确保维度的正确性,可以对矩阵和list进行压缩/降维,比如把list的[[1,2,3]]转换为[1,2,3]
costs = np.squeeze(costs)
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate = 0.000075")
plt.show()
卷积神经网络



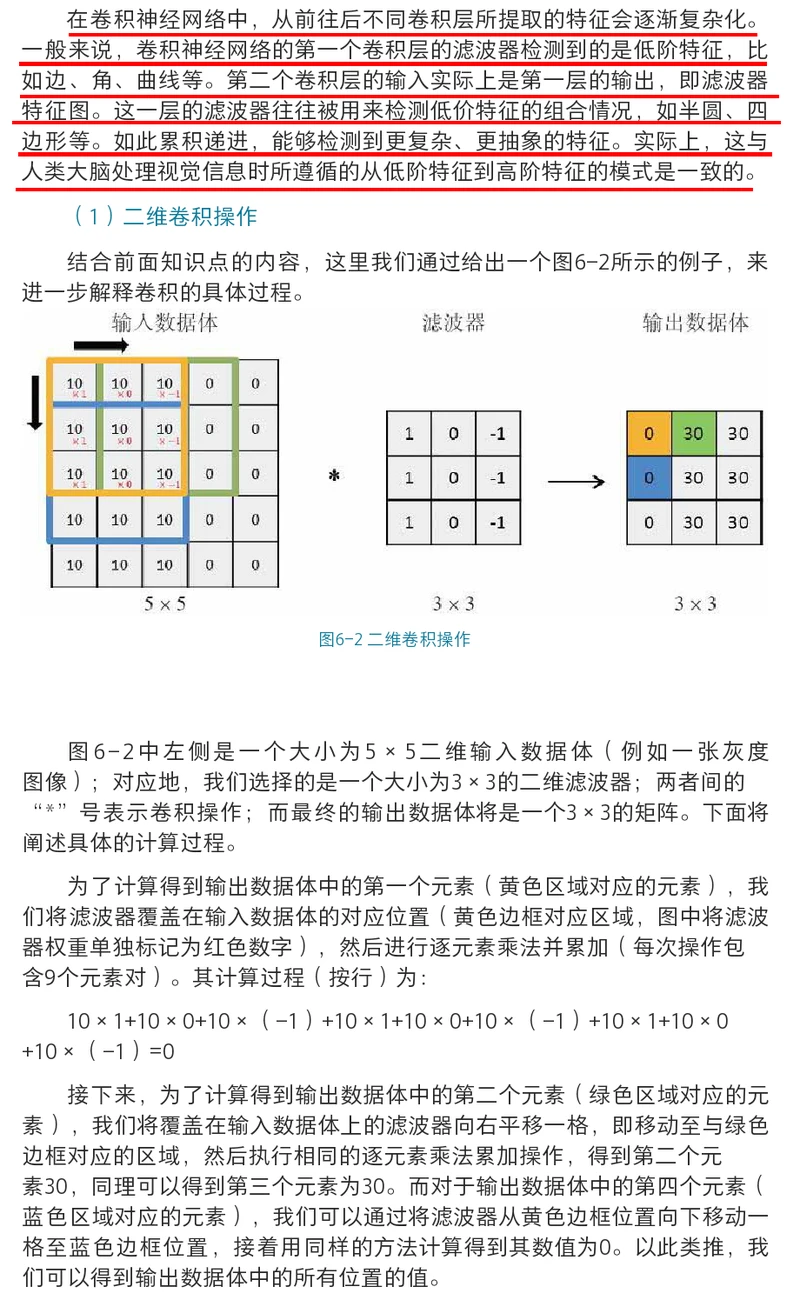
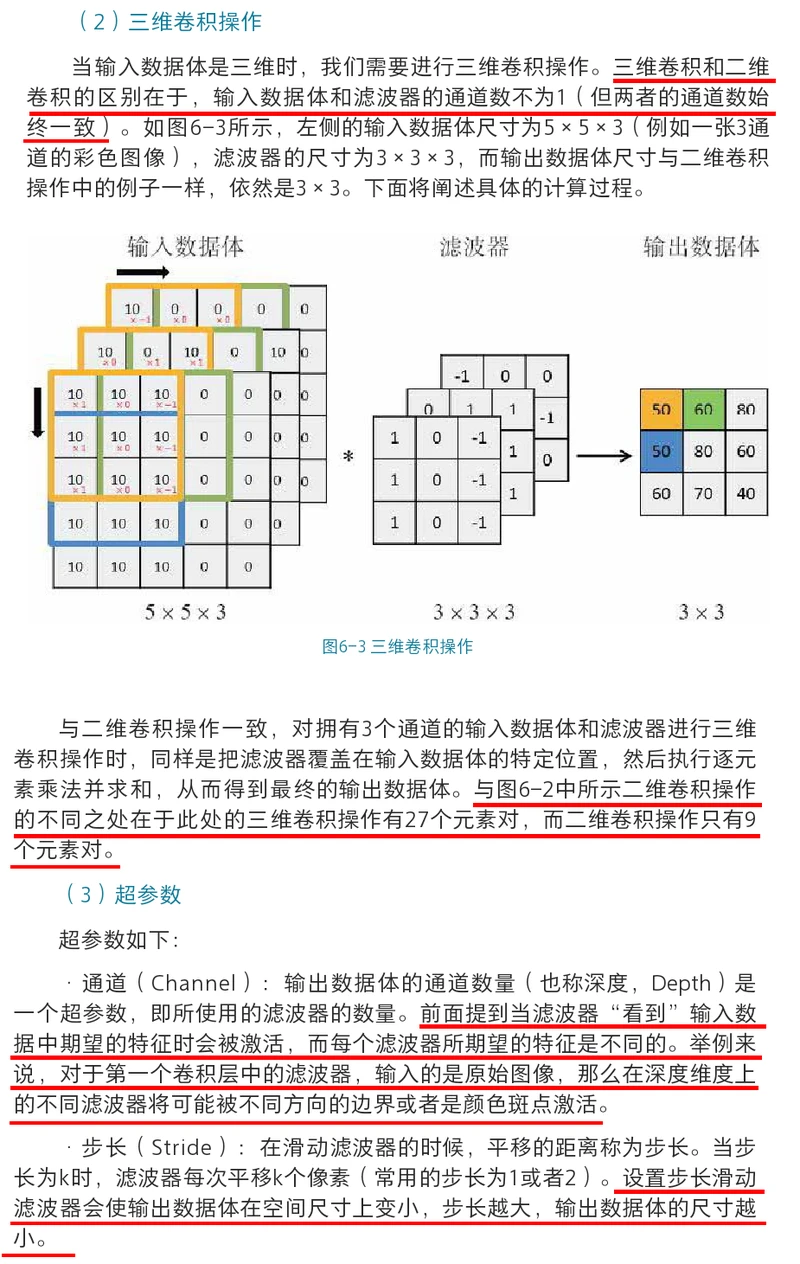
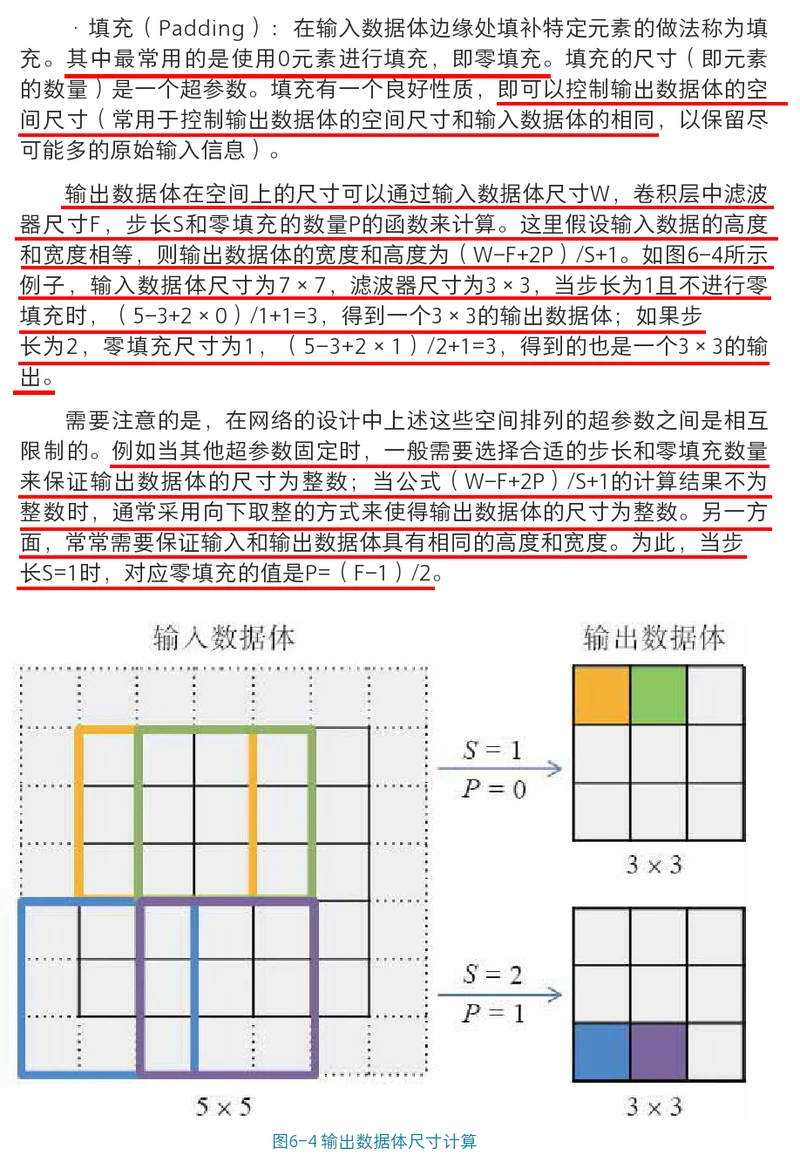

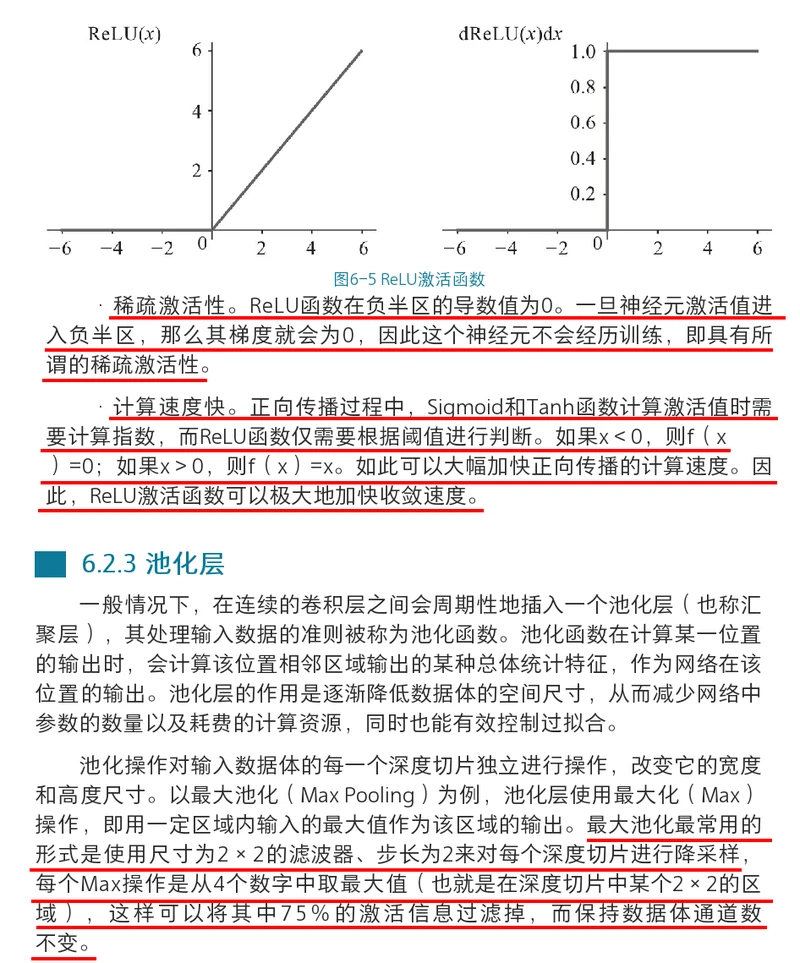

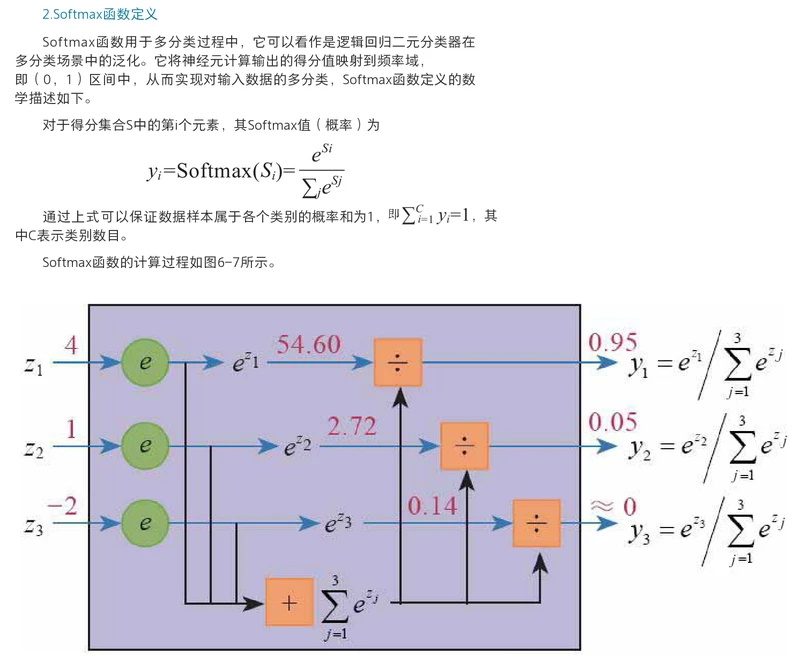

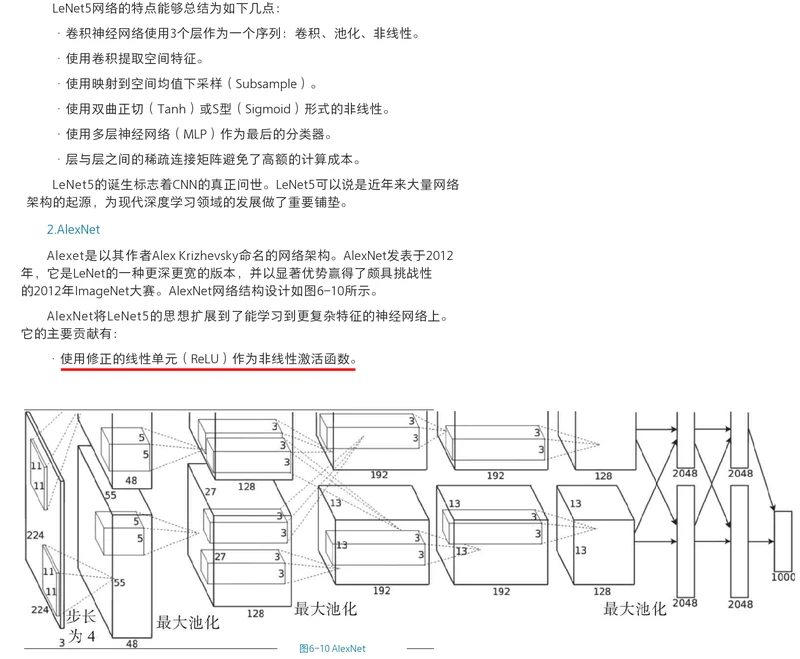
1.输入图像尺寸227*227*3。
2.第一个卷积层的卷积核组的形状应为96*3*11*11。
输出通道数为96,输入通道数为3,单个二维卷积核形状为11*11,步长为3,填充为0。
3.卷积层卷积运算输出单个二维特征图的的运算公式:
假如输入图像的长和宽相等,卷积核的长和宽相等。
(W-F+2P)/S+1:(输入图像长或宽 - 卷积核长或宽 + 2*填充值) / 步长 +1
4.第一个卷积层输出的单个二维特征图的尺寸为(227 - 11 + 2*0) /4 +1 = 55。
第一个卷积层输出的总特征图尺寸为55*55*96。特征图的输出通道数等于卷积核的输出通道数。
第一个卷积层输出的总特征图就拥有55*55*96=290400个神经元。
5.假如不使用卷积网络,则不具有参数共享特征,而使用全连接网络的话,那么举例当特征图的55*55*96=290400个神经元要和一个形状为11*11*3的卷积核进行全连接时,
则每个神经元就要学习11*11*3=363个权重w和1个偏差b,特征图产生的总共要学习的参数数量就有290400*(363+1)=105705600。
6.假如使用卷积网络,则具有参数共享特征,特征图尺寸为55*55*96,那么举例当特征图的55*55*96=290400个神经元要和一个形状为11*11*3的输出通道数为1的卷积核进行全连接时,
每个二维特征图中所有的55*55=3025个神经元都使用相同的363+1个参数,即每个二维特征图都使用不同的363+1个参数,则最后卷积输出一个包含96个神经元的特征图,
产生的总共要学习的参数数量就有96*(363+1)=34944。
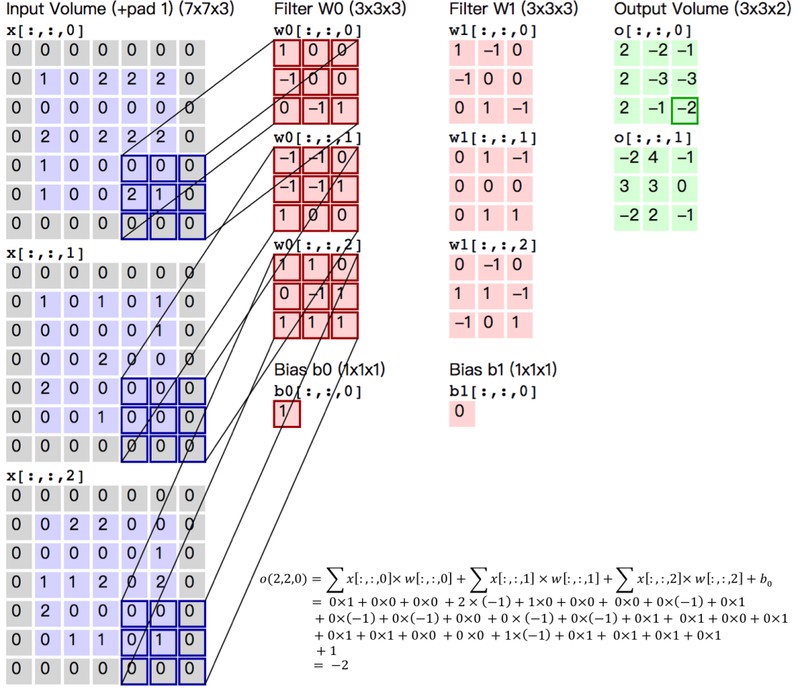


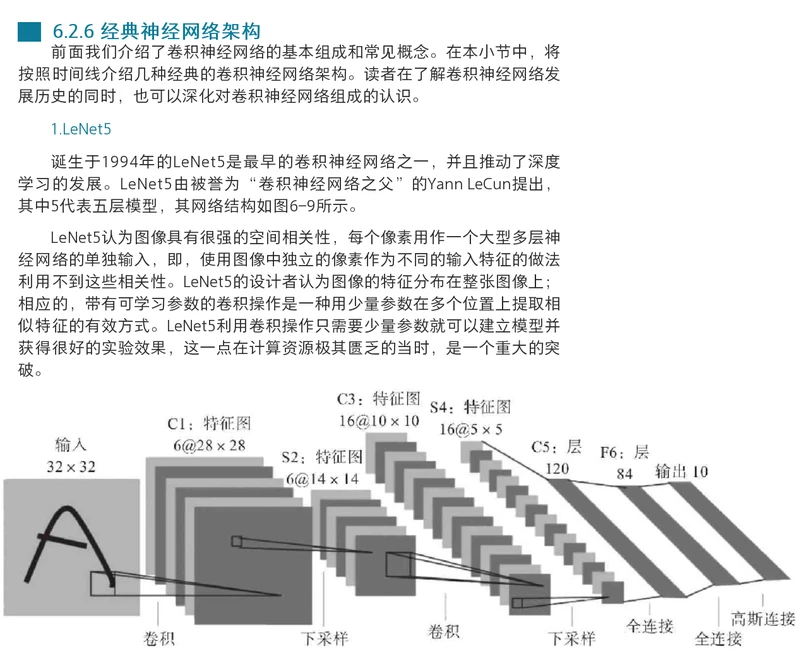




"""
使用paddle框架实现逻辑数字识别案例,关键步骤如下:
1.定义分类器网络结构
2.初始化
3.配置网络结构
4.定义成本函数cost
5.定义优化器optimizer
6.定义事件处理函数
7.进行训练
8.利用训练好的模型进行预测
"""
import os
import matplotlib
#from paddle.v2.plot import Ploter语句引入了PaddlePaddle的绘图工具包,其内部也是调用了matplotlib包。
#在默认设置下,运行绘图代码时可能会遇到“no display name and no$DISPLAY environment variable”的问题。
#这是因为绘图工具函数的默认后端为一些需要图形用户接口(GUI)的后端,而运行的当前环境不满足。
#为此,可加入import matplotlib和matplotlib.use('Agg')语句重新指定不需要GUI的后端,从而解决该问题。
matplotlib.use('Agg')
import numpy as np
import paddle.v2 as paddle
from paddle.v2.plot import Ploter
from PIL import Image
def softmax_regression(img):
"""
定义softmax分类器:只通过一层简单的以softmax为激活函数的全连接层,可以得到分类的结果
Args: img -- 输入的原始图像数据
Return: predict_image -- 分类的结果
"""
predict = paddle.layer.fc(input=img, size=10, act=paddle.activation.Softmax())
return predict
def multilayer_perceptron(img):
"""
定义多层感知机分类器:
含有两个隐藏层(即全连接层)的多层感知器
其中两个隐藏层的激活函数均采用ReLU,输出层的激活函数用Softmax
Args: img -- 输入的原始图像数据
Return: predict_image -- 分类的结果
"""
# 第一个全连接层
hidden1 = paddle.layer.fc(input=img, size=128, act=paddle.activation.Relu())
# 第二个全连接层
hidden2 = paddle.layer.fc(input=hidden1, size=64, act=paddle.activation.Relu())
# 第三个全连接层,需要注意输出尺寸为10,,对应0-9这10个数字
predict = paddle.layer.fc(input=hidden2, size=10, act=paddle.activation.Softmax())
return predict
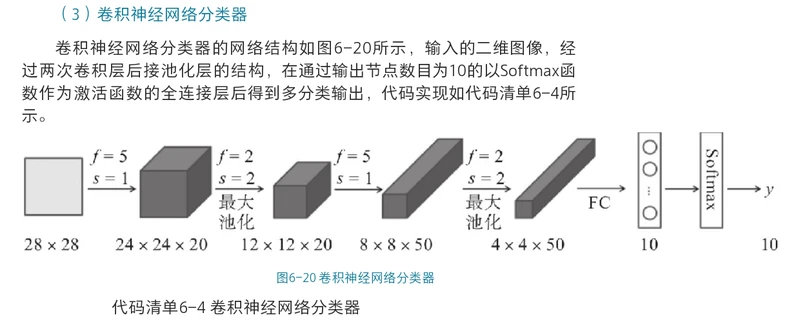
def convolutional_neural_network(img):
"""
定义卷积神经网络分类器:
输入的二维图像,经过两个卷积层+池化层的组合,使用以softmax为激活函数的全连接层作为输出层
Args: img -- 输入的原始图像数据
Return: predict_image -- 分类的结果
"""
# 第一个 卷积层+池化层的组合
conv_pool_1 = paddle.networks.simple_img_conv_pool(
input=img,
filter_size=5, #卷积核大小为5*5
num_filters=20, #卷积核输出通道数为20
num_channel=1, #卷积核输入通道数为1
pool_size=2, #池化层大小为2*2
pool_stride=2, #池化层步幅为2
act=paddle.activation.Relu())
# 第二个 卷积层+池化层的组合
conv_pool_2 = paddle.networks.simple_img_conv_pool(
input=conv_pool_1,
filter_size=5, #卷积核大小为5*5
num_filters=50, #卷积核输出通道数为50
num_channel=20, #卷积核输入通道数为20
pool_size=2, #池化层大小为2*2
pool_stride=2, #池化层步幅为2
act=paddle.activation.Relu())
# 全连接层
predict = paddle.layer.fc(input=conv_pool_2, size=10, act=paddle.activation.Softmax())
return predict

def network_config():
"""
配置网络结构
Return:
images -- 输入层
label -- 标签数据
predict_image -- 输出层
cost -- 损失函数
parameters -- 模型参数
optimizer -- 优化器
"""
# 输入层
# paddle.layer.data:表示数据层
# name=’pixel’:名称为pixel,对应输入图片特征
# type=paddle.data_type.dense_vector(784):数据类型为784维(输入图片的尺寸为28*28)稠密向量
images = paddle.layer.data(name='pixel', type=paddle.data_type.dense_vector(784))
# 标签层
# paddle.layer.data:表示数据层
# name=’label’:名称为label,对应输入图片的类别标签
# type=paddle.data_type.dense_vector(10):数据类型为10维(对应0-9这10个数字)稠密向量
label = paddle.layer.data(name='label', type=paddle.data_type.integer_value(10))
# 选择分类器:卷积神经网络分类器、多层感知机分类器、softmax分类器
# 在此之前已经定义了3种不同的分类器,在下面的代码中,我们可以通过保留某种方法的调用语句、注释掉其余两种,以选择特定的分类器
predict = convolutional_neural_network(images) #卷积神经网络分类器
# predict_image = softmax_regression(images) #softmax分类器
# predict_image = multilayer_perceptron(images) #多层感知机分类器
# 定义成本函数,paddle.layer.classification_cost()函数内部采用的是交叉熵损失函数
cost = paddle.layer.classification_cost(input=predict, label=label)
# 利用cost创建参数parameters
parameters = paddle.parameters.create(cost)
# 创建优化器optimizer,下面列举了2种常用的优化器,不同类型优化器选一即可
# 创建Momentum优化器,并设置学习率(learning_rate)、动量(momentum)和正则化项(regularization)
# 加入动量项Momentum,可以加速更新过程,比如当接近局部最小时,通过震荡作用,跳出局部最小继续下降到全局最小。
# 训练过程在更新权重时采用动量优化器 Momentum ,比如momentum=0.9 代表动量优化每次保持前一次速度的0.9倍。
optimizer = paddle.optimizer.Momentum(
learning_rate=0.01 / 128.0,
momentum=0.9,
regularization=paddle.optimizer.L2Regularization(rate=0.0005 * 128))
# 创建Adam优化器,并设置参数beta1、beta2、epsilon
# optimizer = paddle.optimizer.Adam(beta1=0.9, beta2=0.99, epsilon=1e-06)
config_data = [predict, cost, parameters, optimizer]
return config_data


# 绘图相关标注
TRAIN_TITLE_COST = "Train cost"
TEST_TITLE_COST = "Test cost"
TRAIN_TITLE_ERROR = "Train error rate"
TEST_TITLE_ERROR = "Test error rate"
def plot_init():
"""
绘图初始化函数:初始化绘图相关变量
Return:
cost_ploter -- 用于绘制cost曲线的变量
error_ploter -- 用于绘制error_rate曲线的变量
"""
# 绘制cost曲线所做的初始化设置
cost_ploter = Ploter(TRAIN_TITLE_COST, TEST_TITLE_COST)
# 绘制error_rate曲线所做的初始化设置
error_ploter = Ploter(TRAIN_TITLE_ERROR, TEST_TITLE_ERROR)
ploter = [cost_ploter, error_ploter]
return ploter
def load_image(image_file):
"""
定义读取输入图片的函数:
读取指定路径下的图片,将其处理成分类网络输入数据对应形式的数据,如数据维度等
Args: file -- 输入图片的文件路径
Return: im_data -- 分类网络输入数据对应形式的数据
"""
im_data = Image.open(image_file).convert('L')
im_data = im_data.resize((28, 28), Image.ANTIALIAS)
im_data = np.array(im_data).astype(np.float32).flatten()
im_data = im_data / 255.0
return im_data
def infer(predict, parameters, image_file):
"""
定义判断输入图片类别的函数:
读取并处理指定路径下的图片,然后调用训练得到的模型进行类别预测
Args:
predict_image -- 输出层
parameters -- 模型参数
image_file -- 输入图片的文件路径
"""
# 读取并预处理要预测的图片
test_data = []
cur_dir = os.path.dirname(os.path.realpath(__file__))
test_data.append((load_image(cur_dir + image_file),))
# 利用训练好的分类模型,对输入的图片类别进行预测
probs = paddle.infer(output_layer=predict, parameters=parameters, input=test_data)
#np.argsort(-x) 对数组x中的元素值按照从大到小(降序)的方式返回其元素索引值
lab = np.argsort(-probs)
print "Label of image/infer_3.png is: %d" % lab[0][0]
WITH_GPU = os.getenv('WITH_GPU', '0') != '0' #False
STEP = 0
def main():
"""
主函数:定义神经网络结构,训练模型并打印学习曲线、预测测试数据类别
"""
# 初始化,设置是否使用gpu,trainer数量表示仅使用一个线程进行训练
paddle.init(use_gpu=WITH_GPU, trainer_count=1)
# 定义神经网络结构
predict, cost, parameters, optimizer = network_config()
# 构造trainer,配置三个参数cost、parameters、update_equation,它们分别表示成本函数、参数和更新公式
trainer = paddle.trainer.SGD(cost=cost, parameters=parameters, update_equation=optimizer)
# 初始化绘图变量
cost_ploter, error_ploter = plot_init()
# lists用于存储训练的中间结果,包括cost和error_rate信息,初始化为空
lists = []
def event_handler_plot(event):
"""
定义event_handler_plot事件处理函数:
事件处理器,可以根据训练过程的信息做相应操作:包括绘图和输出训练结果信息
Args:event -- 事件对象,包含event.pass_id, event.batch_id, event.cost等信息
"""
global STEP
if isinstance(event, paddle.event.EndIteration):
# 每训练100次(即100个batch),添加一个绘图点
if STEP % 100 == 0:
cost_ploter.append(TRAIN_TITLE_COST, STEP, event.cost)
# 绘制cost图像,保存图像为‘train_test_cost.png’
cost_ploter.plot('./train_test_cost')
error_ploter.append(TRAIN_TITLE_ERROR, STEP, event.metrics['classification_error_evaluator'])
# 绘制error_rate图像,保存图像为‘train_test_error_rate.png’
error_ploter.plot('./train_test_error_rate')
STEP += 1
# 每训练100个batch,输出一次训练结果信息
if event.batch_id % 100 == 0:
print "Pass %d, Batch %d, Cost %f, %s" % (event.pass_id, event.batch_id, event.cost, event.metrics)
if isinstance(event, paddle.event.EndPass):
# 保存parameters参数保存到文件中
with open('params_pass_%d.tar' % event.pass_id, 'w') as param_f:
trainer.save_parameter_to_tar(param_f)
# 利用测试数据进行测试
result = trainer.test(reader=paddle.batch(paddle.dataset.mnist.test(), batch_size=128))
print "Test with Pass %d, Cost %f, %s\n" % (event.pass_id, result.cost, result.metrics)
# 添加测试数据的cost和error_rate绘图数据
cost_ploter.append(TEST_TITLE_COST, STEP, result.cost)
error_ploter.append(TEST_TITLE_ERROR, STEP, result.metrics['classification_error_evaluator'])
# 存储测试数据的cost和error_rate数据
lists.append((event.pass_id, result.cost, result.metrics['classification_error_evaluator']))
# 训练模型:
# paddle.reader.shuffle(paddle.dataset.mnist.train(), buf_size=8192):
# 表示trainer从paddle.dataset.mnist.train()这个reader中 读取了buf_size=8192大小的数据并打乱顺序
# paddle.batch(reader(), batch_size=128):表示从打乱的数据中再取出batch_size=128大小的数据进行一次迭代训练
# event_handler:事件处理函数,可以自定义event_handler,根据事件信息做相应的操作,下方代码中选择的是event_handler_plot函数
# num_passes:定义训练的迭代次数
trainer.train(
reader=paddle.batch(
paddle.reader.shuffle(paddle.dataset.mnist.train(), buf_size=8192),
batch_size=128),
event_handler=event_handler_plot,
num_passes=10)
# 在多次迭代中,找到在测试数据上表现最好的一组参数,并输出相应信息
best = sorted(lists, key=lambda list: float(list[1]))[0]
print 'Best pass is %s, testing Avgcost is %s' % (best[0], best[1])
print 'The classification accuracy is %.2f%%' % (100 - float(best[2]) * 100)
# 预测输入图片的类型
infer(predict, parameters, '/image/infer_3.png')
if __name__ == '__main__':
main()

"""
使用PaddlePaddle框架实现数字识别案例的预测任务,关键步骤如下:
1.定义分类器网络结构
2.读取训练好的模型参数
3.预测结果
"""
import os
import numpy as np
import paddle.v2 as paddle
from PIL import Image
#False
WITH_GPU = os.getenv('WITH_GPU', '0') != '0'
def softmax_regression(img):
"""
定义softmax分类器:
只通过一层简单的以softmax为激活函数的全连接层,可以得到分类的结果
Args: img -- 输入的原始图像数据
Return: predict_image -- 分类的结果
"""
predict = paddle.layer.fc(input=img, size=10, act=paddle.activation.Softmax())
return predict
def multilayer_perceptron(img):
"""
定义多层感知机分类器:
含有两个隐藏层(即全连接层)的多层感知器
其中两个隐藏层的激活函数均采用ReLU,输出层的激活函数用Softmax
Args: img -- 输入的原始图像数据
Return: predict_image -- 分类的结果
"""
# 第一个全连接层
hidden1 = paddle.layer.fc(input=img, size=128, act=paddle.activation.Relu())
# 第二个全连接层
hidden2 = paddle.layer.fc(input=hidden1, size=64, act=paddle.activation.Relu())
# 第三个全连接层,需要注意输出尺寸为10,,对应0-9这10个数字
predict = paddle.layer.fc(input=hidden2, size=10, act=paddle.activation.Softmax())
return predict
def convolutional_neural_network(img):
"""
定义卷积神经网络分类器:
输入的二维图像,经过两个卷积层+池化层的组合,使用以softmax为激活函数的全连接层作为输出层
Args: img -- 输入的原始图像数据
Return: predict_image -- 分类的结果
"""
# 第一个 卷积层+池化层的组合
conv_pool_1 = paddle.networks.simple_img_conv_pool(
input=img,
filter_size=5, #卷积核大小为5*5
num_filters=20, #卷积核输出通道数为20
num_channel=1, #卷积核输入通道数为1
pool_size=2, #池化层大小为2*2
pool_stride=2, #池化层步幅为2
act=paddle.activation.Relu())
# 第二个 卷积层+池化层的组合
conv_pool_2 = paddle.networks.simple_img_conv_pool(
input=conv_pool_1,
filter_size=5, #卷积核大小为5*5
num_filters=50, #卷积核输出通道数为50
num_channel=20, #卷积核输入通道数为20
pool_size=2, #池化层大小为2*2
pool_stride=2, #池化层步幅为2
act=paddle.activation.Relu())
# 全连接层
predict = paddle.layer.fc(input=conv_pool_2, size=10, act=paddle.activation.Softmax())
return predict
def network_config():
"""
配置网络结构
Return: predict_image -- 输出层
"""
# 输入层
# paddle.layer.data表示数据层,name=’pixel’:名称为pixel,对应输入图片特征
# type=paddle.data_type.dense_vector(784):数据类型为784维(输入图片的尺寸为28*28)稠密向量
images = paddle.layer.data(name='pixel', type=paddle.data_type.dense_vector(784))
# 选择分类器:卷积神经网络分类器、多层感知机分类器、softmax分类器
# 在此之前已经定义了3种不同的分类器,在下面的代码中,我们可以通过保留某种方法的调用语句、注释掉其余两种,以选择特定的分类器
predict = convolutional_neural_network(images) # 卷积神经网络分类器
# predict_image = softmax_regression(images) #softmax分类器
# predict_image = multilayer_perceptron(images) #多层感知机分类器
return predict
def load_image(image_file):
"""
定义读取输入图片的函数:
读取指定路径下的图片,将其处理成分类网络输入数据对应形式的数据,如数据维度等
Args: file -- 输入图片的文件路径
Return: img_data -- 分类网络输入数据对应形式的数据
"""
img_data = Image.open(image_file).convert('L')
img_data = img_data.resize((28, 28), Image.ANTIALIAS)
img_data = np.array(img_data).astype(np.float32).flatten()
img_data = img_data / 255.0
return img_data
def main():
"""
定义网络结构、读取模型参数并预测结果
"""
paddle.init(use_gpu=WITH_GPU)
# 定义神经网络结构
predict = network_config()
# 读取模型参数
if not os.path.exists('params_pass_9.tar'):
print "Params file doesn't exists."
return
with open('params_pass_9.tar', 'r') as param_f:
parameters = paddle.parameters.Parameters.from_tar(param_f)
# 读取并预处理要预测的图片
test_data = []
cur_dir = os.path.dirname(os.path.realpath(__file__))
test_data.append((load_image(cur_dir + '/image/infer_3.png'),))
# 利用训练好的分类模型,对输入的图片类别进行预测
probs = paddle.infer(output_layer=predict, parameters=parameters, input=test_data)
lab = np.argsort(-probs)
print "Label of image/infer_3.png is: %d" % lab[0][0]
if __name__ == '__main__':
main()

Jupyter文件中的内容



配置说明
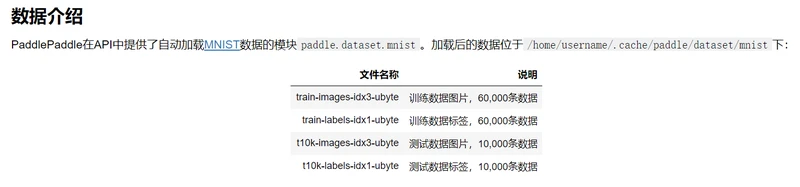
1.首先,加载PaddlePaddle的V2 api包。
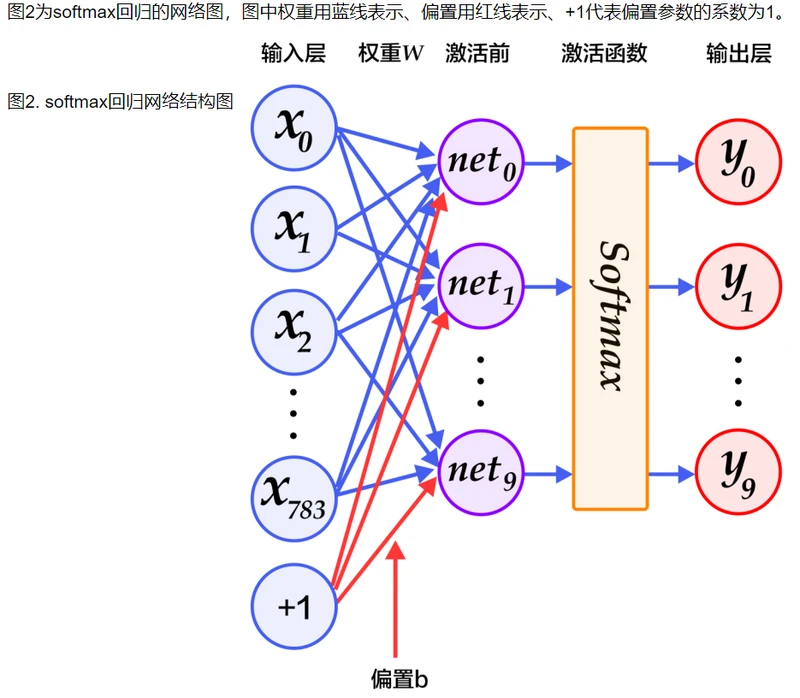
2.定义softmax分类器
def softmax_regression(img):
"""
定义softmax分类器:只通过一层简单的以softmax为激活函数的全连接层,可以得到分类的结果
Args: img -- 输入的原始图像数据
Return: predict_image -- 分类的结果
"""
predict = paddle.layer.fc(input=img, size=10, act=paddle.activation.Softmax())
return predict
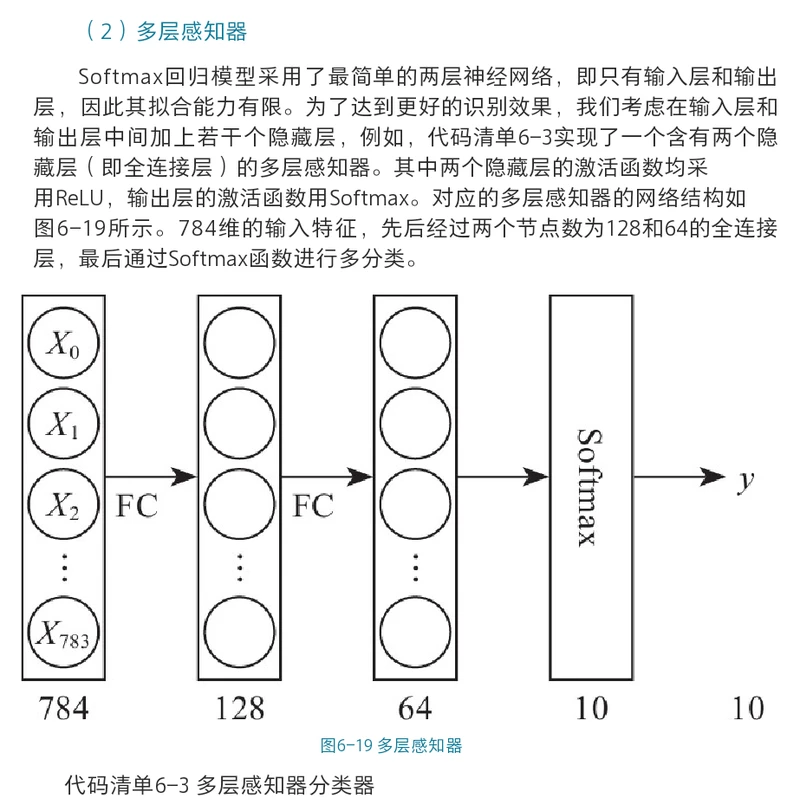
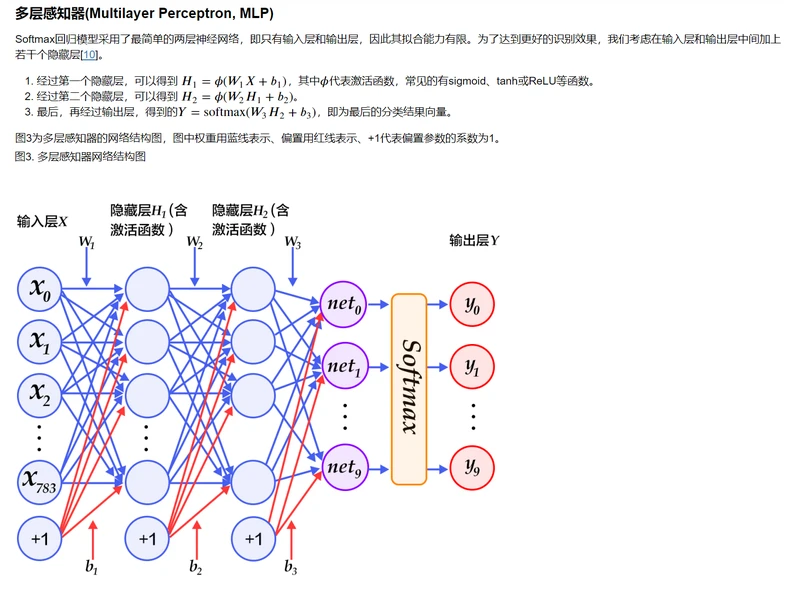
3.多层感知器:下面代码实现了一个含有两个隐藏层(即全连接层)的多层感知器。其中两个隐藏层的激活函数均采用ReLU,输出层的激活函数用Softmax。
def multilayer_perceptron(img):
# 第一个全连接层,激活函数为ReLU
hidden1 = paddle.layer.fc(input=img, size=128, act=paddle.activation.Relu())
# 第二个全连接层,激活函数为ReLU
hidden2 = paddle.layer.fc(input=hidden1, size=64, act=paddle.activation.Relu())
# 以softmax为激活函数的全连接输出层,输出层的大小必须为数字的个数10
predict = paddle.layer.fc(input=hidden2, size=10, act=paddle.activation.Softmax())
return predict
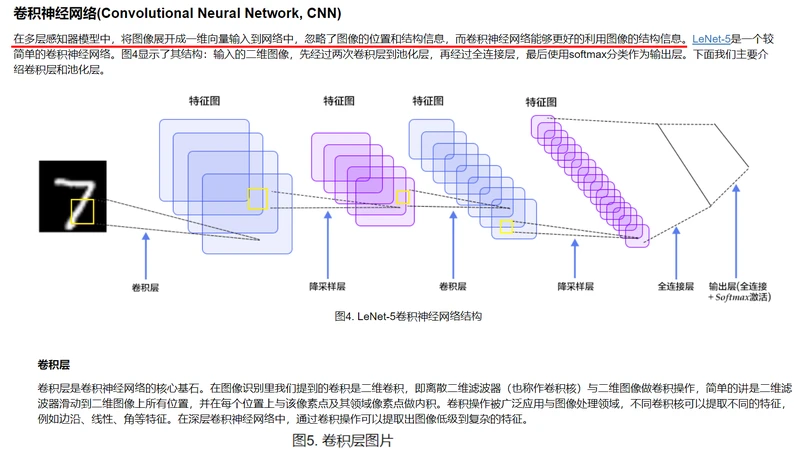
4.卷积神经网络LeNet-5: 输入的二维图像,首先经过两次卷积层到池化层的组合,再经过全连接层,最后使用以softmax为激活函数的全连接层作为输出层。
def convolutional_neural_network(img):
# 第一个 卷积层+池化层的组合
conv_pool_1 = paddle.networks.simple_img_conv_pool(
input=img,
filter_size=5, #卷积核大小为5*5
num_filters=20, #卷积核输出通道数为20
num_channel=1, #卷积核输入通道数为1
pool_size=2, #池化层大小为2*2
pool_stride=2, #池化层步幅为2
act=paddle.activation.Relu())
# 第二个 卷积层+池化层的组合
conv_pool_2 = paddle.networks.simple_img_conv_pool(
input=conv_pool_1,
filter_size=5, #卷积核大小为5*5
num_filters=50, #卷积核输出通道数为50
num_channel=20, #卷积核输入通道数为20
pool_size=2, #池化层大小为2*2
pool_stride=2, #池化层步幅为2
act=paddle.activation.Relu())
# 以softmax为激活函数的全连接输出层,输出层的大小必须为数字的个数10
predict = paddle.layer.fc(input=conv_pool_2, size=10, act=paddle.activation.Softmax())
return predict
5.接着,通过layer.data调用来获取数据,然后调用分类器(这里我们提供了三个不同的分类器)得到分类结果。
训练时,对该结果计算其损失函数,分类问题常常选择交叉熵损失函数。
# 该模型运行在单个CPU上
paddle.init(use_gpu=False, trainer_count=1)
images = paddle.layer.data(name='pixel', type=paddle.data_type.dense_vector(784))
label = paddle.layer.data(name='label', type=paddle.data_type.integer_value(10))
# predict = softmax_regression(images) # Softmax回归
# predict = multilayer_perceptron(images) #多层感知器
predict = convolutional_neural_network(images) #LeNet5卷积神经网络
cost = paddle.layer.classification_cost(input=predict, label=label)
6.然后,指定训练相关的参数。
训练方法(optimizer):代表训练过程在更新权重时采用动量优化器 Momentum ,其中参数0.9代表动量优化每次保持前一次速度的0.9倍。
训练速度(learning_rate):迭代的速度,与网络的训练收敛速度有关系。
正则化(regularization):是防止网络过拟合的一种手段,此处采用L2正则化。
parameters = paddle.parameters.create(cost)
# 加入动量项Momentum,可以加速更新过程,比如当接近局部最小时,通过震荡作用,跳出局部最小继续下降到全局最小。
# 训练过程在更新权重时采用动量优化器 Momentum ,比如momentum=0.9 代表动量优化每次保持前一次速度的0.9倍。
optimizer = paddle.optimizer.Momentum(
learning_rate=0.1 / 128.0,
momentum=0.9,
regularization=paddle.optimizer.L2Regularization(rate=0.0005 * 128))
trainer = paddle.trainer.SGD(cost=cost, parameters=parameters, update_equation=optimizer)
7.下一步,我们开始训练过程。paddle.dataset.movielens.train() 和 paddle.dataset.movielens.test()分别做训练和测试数据集。
这两个函数各自返回一个reader——PaddlePaddle中的reader是一个Python函数,每次调用的时候返回一个Python yield generator。
下面shuffle是一个reader decorator,它接受一个reader A,返回另一个reader B —— reader B 每次读入buffer_size条训练数据到一个buffer里,
然后随机打乱其顺序,并且逐条输出。
batch是一个特殊的decorator,它的输入是一个reader,输出是一个batched reader —— 在PaddlePaddle里,一个reader每次yield一条训练数据,
而一个batched reader每次yield一个mini batch。
event_handler_plot可以用来在训练过程中画图如下: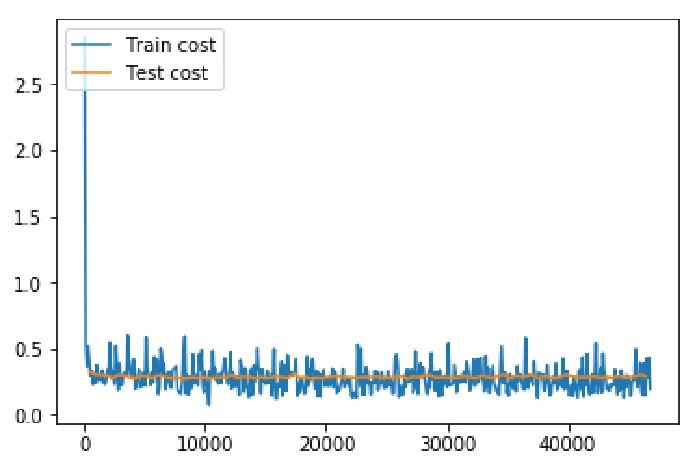
from paddle.v2.plot import Ploter
train_title = "Train cost"
test_title = "Test cost"
cost_ploter = Ploter(train_title, test_title)
step = 0
# event_handler to plot a figure
def event_handler_plot(event):
global step
if isinstance(event, paddle.event.EndIteration):
if step % 100 == 0:
cost_ploter.append(train_title, step, event.cost)
cost_ploter.plot()
step += 1
if isinstance(event, paddle.event.EndPass):
# save parameters
with open('params_pass_%d.tar' % event.pass_id, 'w') as f:
parameters.to_tar(f)
result = trainer.test(reader=paddle.batch(paddle.dataset.mnist.test(), batch_size=128))
cost_ploter.append(test_title, step, result.cost)
event_handler 用来在训练过程中输出训练结果
lists = []
def event_handler(event):
if isinstance(event, paddle.event.EndIteration):
if event.batch_id % 100 == 0:
print "Pass %d, Batch %d, Cost %f, %s" % (event.pass_id, event.batch_id, event.cost, event.metrics)
if isinstance(event, paddle.event.EndPass):
# save parameters
with open('params_pass_%d.tar' % event.pass_id, 'w') as f:
parameters.to_tar(f)
result = trainer.test(reader=paddle.batch(paddle.dataset.mnist.test(), batch_size=128))
print "Test with Pass %d, Cost %f, %s\n" % (event.pass_id, result.cost, result.metrics)
lists.append((event.pass_id, result.cost, result.metrics['classification_error_evaluator']))
trainer.train(
reader=paddle.batch(
paddle.reader.shuffle(paddle.dataset.mnist.train(), buf_size=8192),
batch_size=128),
event_handler=event_handler_plot,
num_passes=5)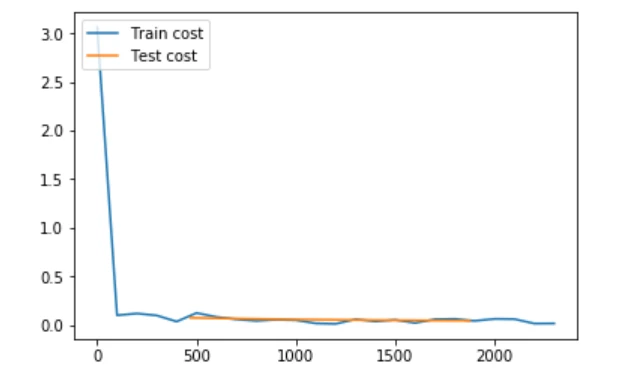
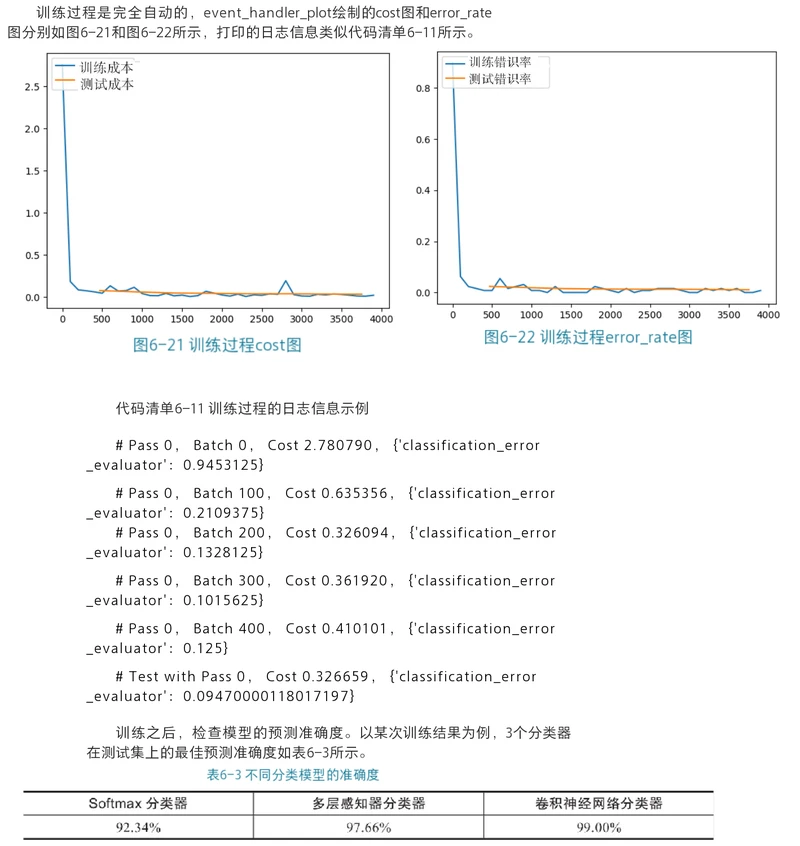
训练过程是完全自动的,event_handler里打印的日志类似如下所示:
# Pass 0, Batch 0, Cost 2.780790, {'classification_error_evaluator': 0.9453125}
# Pass 0, Batch 100, Cost 0.635356, {'classification_error_evaluator': 0.2109375}
# Pass 0, Batch 200, Cost 0.326094, {'classification_error_evaluator': 0.1328125}
# Pass 0, Batch 300, Cost 0.361920, {'classification_error_evaluator': 0.1015625}
# Pass 0, Batch 400, Cost 0.410101, {'classification_error_evaluator': 0.125}
# Test with Pass 0, Cost 0.326659, {'classification_error_evaluator': 0.09470000118017197}
训练之后,检查模型的预测准确度。用 MNIST 训练的时候,一般 softmax回归模型的分类准确率为约为 92.34%,多层感知器为97.66%,
卷积神经网络可以达到 99.20%。
2.应用模型
可以使用训练好的模型对手写体数字图片进行分类,下面程序展示了如何使用paddle.infer接口进行推断。
from PIL import Image
import numpy as np
import os
def load_image(file):
im = Image.open(file).convert('L')
im = im.resize((28, 28), Image.ANTIALIAS)
im = np.array(im).astype(np.float32).flatten()
im = im / 255.0
return im
test_data = []
cur_dir = os.getcwd()
test_data.append((load_image(cur_dir + '/image/infer_3.png'),))
probs = paddle.infer(output_layer=predict, parameters=parameters, input=test_data)
lab = np.argsort(-probs) # probs and lab are the results of one batch data
print "Label of image/infer_3.png is: %d" % lab[0][0] #Label of image/infer_3.png is: 3

