目录
1 背景
2 浅水运动
3 二维浅水方程的推导
3.1 连续性方程
3.2 运动方程
4 总结
1 背景
在前面的文章中,我们介绍了适用于不可压缩牛顿流体的N-S方程。在实际的水动力学模拟中,除非我们需要研究具体的流动形态,在一般的河道水动力学模拟中,我们多关注水深、流速、流量的变化,且水深相对较浅,因此采用二维数学模型即可。
在本文中,我们介绍如何从三维模型沿水深积分平均获得二维模型。
2 浅水运动
浅水运动具有以下特点:
- 缓变流,具有自由表面;
- 以重力为主要驱动力,水流与固壁之间及水流内部的摩擦力为主要耗散力;
- 水平流速沿垂线近似均匀分布,不考虑实际存在的对数或者指数形式的垂线流速分布;
- 水平运动尺度远大于垂直运动尺度,垂向加速度可以忽略,水压力接近静压分布(波长比水深大得多)。
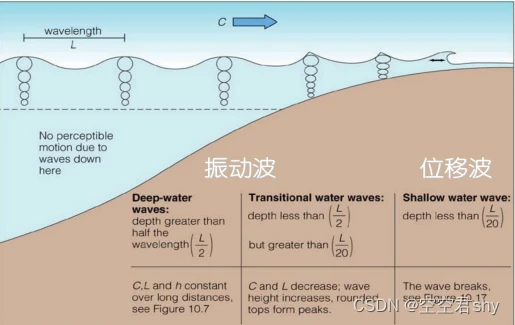
具体来说,需要满足下面几条要求:
- 水深相对较浅 (如内陆河道中,而非海洋中);
- 水底坡度较缓;
- 水面渐变且坡度较缓;
- 无明显垂直环流。
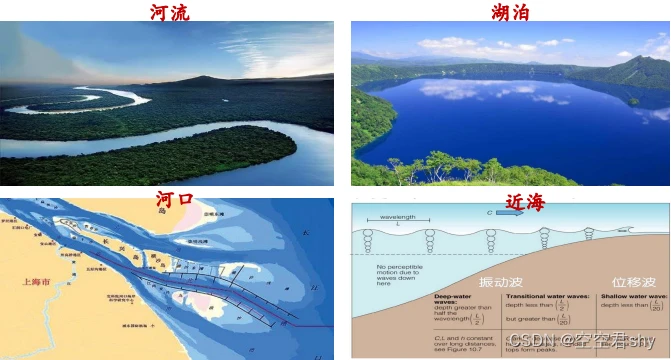
满足浅水假设的水体有:河流、湖泊、近海与河口等。
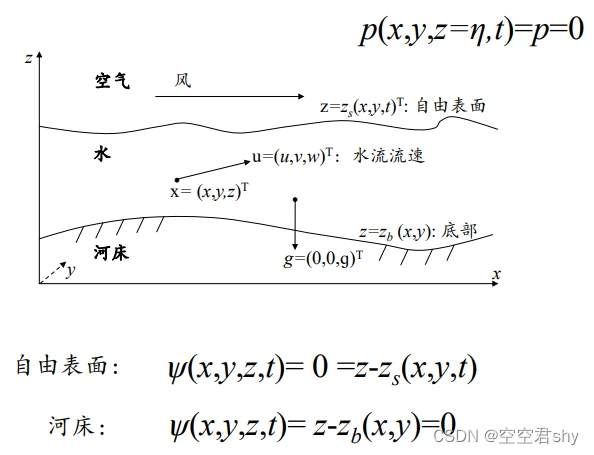
3 二维浅水方程的推导
前面的文章中我们介绍过,对N-S方程进行雷诺平均得到RANS方程如下
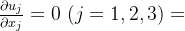
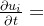
其中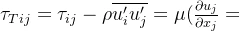
上面式子中的ui与压力p均为时均值。
接下来我们对物理量在水深方向进行积分平均
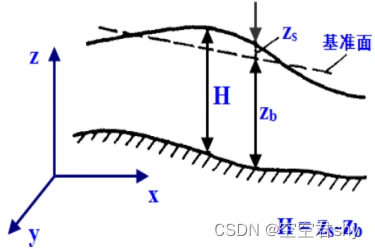
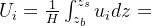
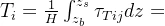
引入牛顿-莱布尼兹公式
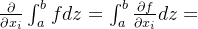
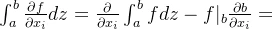
引入自由表面的运动学条件
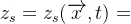
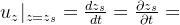
引入底部运动学条件
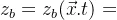
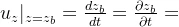
3.1 连续性方程
对连续性方程沿水深方向进行积分
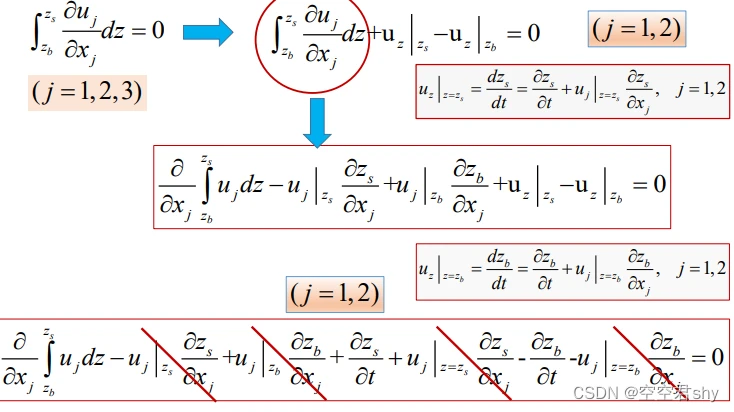
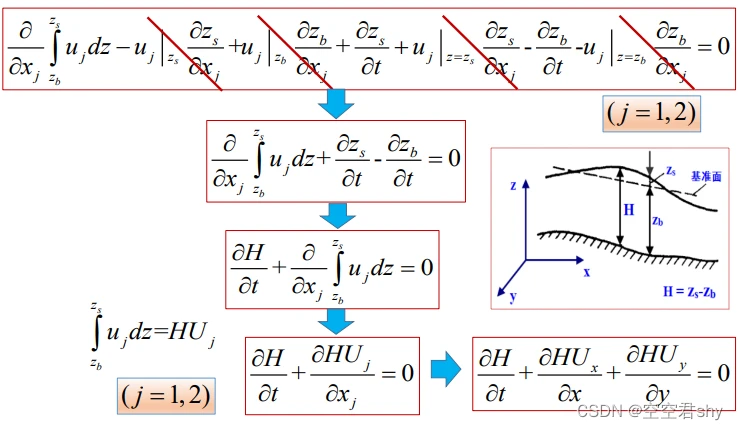
得到二维水流连续性方程为
其中h为水深,ux为沿x方向流速,uy为沿y方向流速。
3.2 运动方程
运动方程沿水深方向进行积分
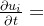
该方程左边第一项为非定常项,第二项为对流项,右边第二项为压力项,第三项为扩散项。扩散项包括粘性扩散和紊动扩散。下面根据每一项进行积分平均。
首先是非定常项:
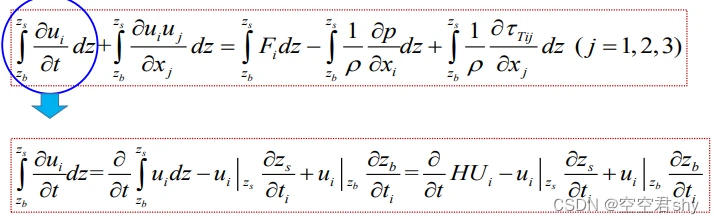
压力项沿垂线平均:

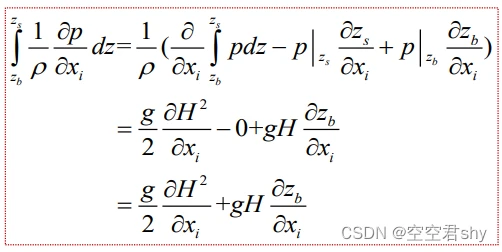
扩散项沿垂线平均:


对流项沿垂线平均:

在这一步后,若不引入动量修正系数,将流速沿水深方向分布不均匀的项单独列出,则是常见的二次流项。 关于二次流项如何计算,目前已经有很多相关研究,常用的是将其视为旋流强度的函数。在关注二次流的情况下,如研究河段的曲率较大时,我们需要单独考虑二次流项。若河段较为顺直,二次流并不明显时,我们可以引入动量修正系数,将该问题进行化简。
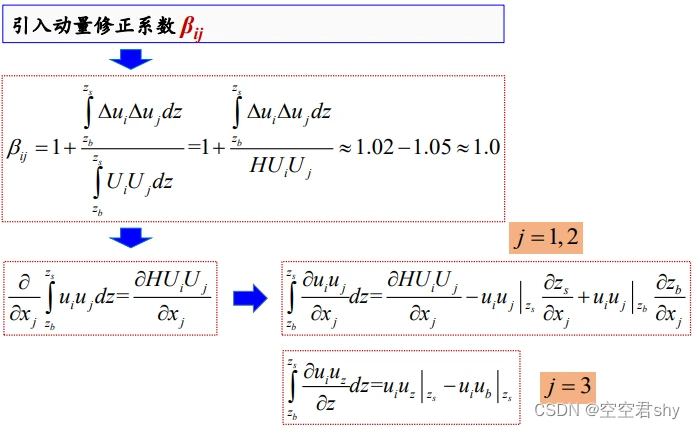
综上,我们便得到了二维浅水方程的运动方程
其中τs为风应力,如果计算工况风应力较小的话可以忽略该项;τb为河床阻力项,可以用曼宁公式进行计算。
其中Tij为切应力,包括粘性切应力和紊动切应力。由于分子之间粘性切应力比较小,常常可以忽略,仅保留紊动切应力。类似于粘性切应力的表达,采用二维的可莫哥洛夫假设,紊动切应力写为
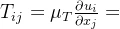 , μ为u紊动动力粘滞系数。
, μ为u紊动动力粘滞系数。
4 总结
以上我们就从三维的雷诺平均方程(RANS方程)出发得到了二维浅水方程。该方程广泛应用于河道、河口、湖泊的水动力学模拟。
还应注意,上面的方程建立的前提是密度变化可以忽略,前面的文章中我们也介绍过,对于含沙水流而言,质量含沙量低于200kg/m³时我们可以忽略密度的变化,若为高含沙水流则不应忽略。在使用时应当注意。

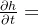
![\frac{\partial }{\partial t}hu_x + \frac{\partial hu_xu_x}{x} + \frac{\partial hu_xu_y}{\partial y} = -\frac{g}{2}\frac{\partial h^2}{\partial x}-gh\frac{\partial z_b}{\partial x} + \frac{1}{\rho}[\frac{\partial (hT_{xx})}{\partial x} + \frac{\partial (hT_{xy})}{\partial y}] + \tau _{sx} -\tau _{bx}](https://yyzqsoft.com/uploads/202407/04/12e7c7be7e5e6ed6.webp)
![\frac{\partial }{\partial t}hu_y + \frac{\partial hu_yu_x}{x} + \frac{\partial hu_yu_y}{\partial y} = -\frac{g}{2}\frac{\partial h^2}{\partial y}-gh\frac{\partial z_b}{\partial y} + \frac{1}{\rho}[\frac{\partial (hT_{yy})}{\partial y} + \frac{\partial (hT_{yx})}{\partial x}] + \tau _{sy} -\tau _{by}](https://yyzqsoft.com/uploads/202407/04/50ad5c32e21db821.webp)