
投资小课堂由开课啦????
1、期权类型与到期盈亏
2、定价模型与平价关系式
3、期权价格和相关变量的关系
期权的希腊字母主要包括 Delta、 Gamma、 Theta、Vega 和 Rho,每个希腊字母都是用来度量期权头寸的某种特定风险,金融机构通过管理期权的这些希腊字母数值,从而使期权的风险控制在可承受的范围之内。
一、期权的 Delta
期权的 Delta 被定义为期权价格变动与基础资产价格变动的比率,也就是期权价格与基础资产价格之间关系曲线的切线斜率。比如,期权Dela值等于0.6就意味着当基础资产价格变化一个很小的金额时,相应的期权价格变化约等于基础资产价格变化的60%。
Delta的计算
def delta_option(S,K,sigma,r,T,optype, positype):
'''计算欧式期权的Delta值
S 基础资产价格
K 行权价
sigma 基础资产价格百分比变化的波动率
r 无风险收益率
T 期权剩余时间(年)
optype 期权类型;'call'看涨,'put'看跌
positype 期权头寸方向;'long'多头,'short'空头
'''
d1 = (np.log(S/K) + (r+pow(sigma,2)/2)*T) / (sigma*np.sqrt(T))
if optype=='call':
if positype=='long':
delta = norm.cdf(d1)
else:
delta = -norm.cdf(d1)
else:
if positype=='long':
delta = norm.cdf(d1)-1
else:
delta = 1-norm.cdf(d1)
return delta
例1:
以某只股票的期权为例,假设股票当前价格是5元/股,执行价格6元,波动率24%,无风险收益4%,剩余时间为6个月,计算看涨期权多头的方式为:
delta_option(S=5, K=6, sigma=0.24, r=0.04, T=0.5, optype='call', positype='long')
# 输出
>>> 0.1917034562582849
基础资产价格与Delta的关系
仍用例1股票为例,观察股票价格与Delta的关系
S_list = np.linspace(4.0, 8.0, 100)
Delta_call = delta_option(S_list, K=6, sigma=0.24, r=0.04, T=0.5, optype='call', positype='long')
Delta_put = delta_option(S_list, K=6, sigma=0.24, r=0.04, T=0.5, optype='put', positype='long')
plt.figure(figsize=(8,6))
plt.plot(S_list, Delta_call, 'b-', label='看涨期权多头', lw=2.5)
plt.plot(S_list, Delta_put, 'r-', label='看跌期权多头', lw=2.5)
plt.xlabel('股票价格', fontsize=13)
plt.ylabel('Delta', fontsize=13, rotation=90)
plt.xticks(fontsize=13)
plt.yticks(fontsize=13)
plt.ylim(-1.0, 1.0)
plt.title('股票价格与期权多头Delta的关系', fontsize=14)
plt.legend(fontsize=13)
plt.grid('True');
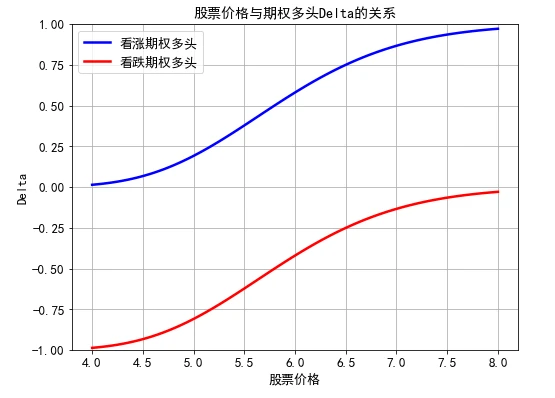
上图显示了看涨与看跌期权的 Delta值与基础资产价格之间的变化关系。从图中可以梳理出3个特征:一是当基础资产价格增大的时候,期权的Dela值会增加;二是曲线的斜率始终是正的,用后面讨论的期权 Gamma值来描述就是期权的 Gamma值始终为正;三是当基础资产价格小于期权执行价格(6元/股)时,随着基础资产价格的增大,曲线的斜率递增;相反,当基础资产价格大于执行价格时,曲线的斜率递减。
期权期限与期权Delta的关系
仍用例1股票为例,观察期权期限与Delta的关系
T_list = np.linspace(0.1, 5.0, 100)
Delta_call1 = delta_option(S=7, K=6, sigma=0.24, r=0.04, T=T_list, optype='call', positype='long')
Delta_call2 = delta_option(S=6, K=6, sigma=0.24, r=0.04, T=T_list, optype='call', positype='long')
Delta_call3 = delta_option(S=5, K=6, sigma=0.24, r=0.04, T=T_list, optype='call', positype='long')
plt.figure(figsize=(8,6))
plt.plot(T_list, Delta_call1, 'b-', label='实值看涨期权多头', lw=2.5)
plt.plot(T_list, Delta_call2, 'r-', label='平值看涨期权多头', lw=2.5)
plt.plot(T_list, Delta_call3, 'g-', label='虚值看涨期权多头', lw=2.5)
plt.xlabel('期权期限', fontsize=13)
plt.ylabel('Delta', fontsize=13, rotation=90)
plt.xticks(fontsize=13)
plt.yticks(fontsize=13)
plt.title('期权期限与期权多头Delta的关系', fontsize=14)
plt.legend(fontsize=13)
plt.grid('True');
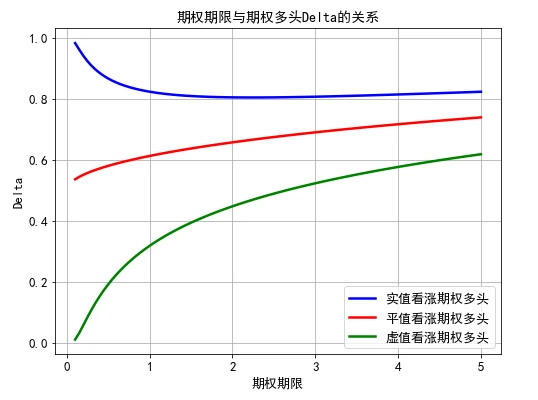
上图中有3条曲线,由上往下的第1条曲线表示实值看涨期权多头的Delta值与期权期限之间的关系,这条曲线的特点是随着期权期限的增加,实值看涨期权的 Delta值是先递减然后再缓慢递增;第2条曲线、第3条曲线分别表示平值、虚值看涨期权多头的Delta值与期权期限之间的关系,显然平值、虚值期权的 Delta值均是期权期限的递增函数,但是虚值期权 Delta值的边际增量则大于平价期权。期权空头的希腊字母可以通过对期权多头的希腊字母取相反数直接得到,再此就不再赘述。
二、期权的Gamma
期权的 Gamma(r)是指期权Delta值的变化与基础资产价格变化的比率。Gamma是期权价值关于基础资产价格的二阶偏导数。比如,期权 Gamma等于0.3,这就意味着当基础资产价格变化时,相应期权Delta值的变化约等于基础资产价格变化的30%。
Gamma的计算
def gamma_option(S,K,sigma,r,T):
'''计算欧式期权的gamma值
S 期权基础资产的价格
K 期权行权价
sigma 基础资产价格百分比变化的波动率
r 无风险收益率
T 期权合约剩余时间(年)
'''
d1 = (np.log(S/K) + (r+pow(sigma,2)/2)*T) / (sigma*np.sqrt(T))
return np.exp(-pow(d1,2)/2) / (S*sigma*np.sqrt(2*np.pi*T))
还是以例1的股票为例子,计算其Gamma值
gamma_option(S=5,K=6,sigma=0.24, r=0.04, T=0.5)
# 输出
>>> 0.32156316870552004
基础资产价格与Gamma的关系
用例1股票为例,观察股票价格与Gamma的关系
S_list = np.linspace(4.0, 8.0, 100)
gamma_list1 = gamma_option(S=S_list, K=6, sigma=0.24, r=0.04, T=0.5)
plt.figure(figsize=(8,6))
plt.plot(S_list, gamma_list1, 'b-', lw=2.5)
plt.xlabel('股票价格', fontsize=13)
plt.ylabel('Gamma', fontsize=13, rotation=90)
plt.xticks(fontsize=13)
plt.yticks(fontsize=13)
plt.title('股票价格与Gamma的关系', fontsize=14)
# plt.legend(fontsize=13)
plt.grid('True');
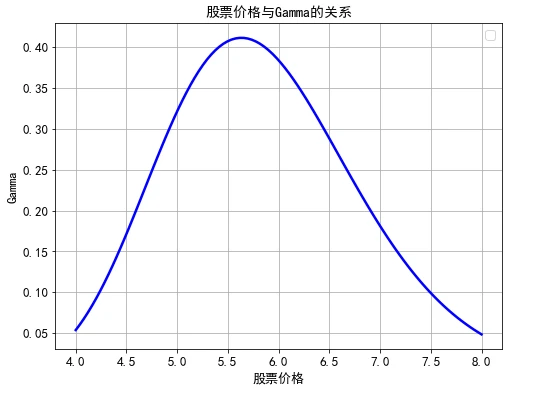
上图中的曲线展示了期权的 Gamma与基础资产价格之间的变化关系,这条曲线比较接近于正态分布曲线,并且该曲线可以分为两段,第1段是基础资产价格显著小于期权执行价格,也就是看涨期权是深度虚值、看跌期权是深度实值,期权Gamma是基础资产价格的递增函数;第2段是基础资产价格略小于和大于期权执行价格,期权 Gamma是基础资产价格的递减函数。此外,当期权接近于平价期权时,也就是基础资产价格接近于期权执行价格时,期权 Gamma值最大。
期权期限与Gamma的关系
仍用例1股票为例,观察期权期限与Gamma的关系
T_list = np.linspace(0.1, 5.0, 100)
gamma1 = gamma_option(S=7, K=6, sigma=0.24, r=0.04, T=T_list)
gamma2 = gamma_option(S=6, K=6, sigma=0.24, r=0.04, T=T_list)
gamma3 = gamma_option(S=5, K=6, sigma=0.24, r=0.04, T=T_list)
plt.figure(figsize=(8,6))
plt.plot(T_list, gamma1, 'b-', label='实值看涨期权多头', lw=2.5)
plt.plot(T_list, gamma2, 'r-', label='平值看涨期权多头', lw=2.5)
plt.plot(T_list, gamma3, 'g-', label='虚值看涨期权多头', lw=2.5)
plt.xlabel('期权期限', fontsize=13)
plt.ylabel('Gamma', fontsize=13, rotation=90)
plt.xticks(fontsize=13)
plt.yticks(fontsize=13)
plt.ylim(0, 0.9)
plt.title('期权期限与Gamma的关系', fontsize=14)
plt.legend(fontsize=13)
plt.grid('True');
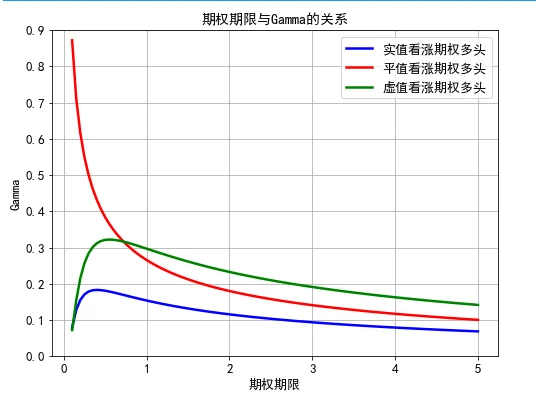
上图显示了平价期权、虚值期权和实值期权的 Gamma与期权期限的关系。图中有3条曲线,从上往下的第1条是平价期权,第2条是虚值期权,第3条是实值期权。对于平价期权而言, Gamma是期权期限的递减函数;同时,期限短的平价期权 Gamma很高,这意味着越接近合约到期日,平价期权的 Delta值对于基础资产价格变动越敏感。此外,无论对于虚值期权还是实值期权,当期权期限比较短时, Gamma是期限的递增函数;当期限拉长时,Gamma则变成了期限的递减函数。
三、期权的Theta
期权的 Theta 定义为在其他条件不变时,期权价值变化与时间变化的比率。Theta有时也被称为期权的时间损耗( time decay),在其他条件不变的情况下,不论是看涨期权还是看跌期权,通常距离期权到期日越远,期权价值是越高的;距离期权到期日越近,期权价值则是越低的。所以在期权领域有这样一句话:“对于期权的多头而言,时间流逝是敌人,对于期权的空头而言,时间流逝是密友“
Theta的计算
def theta_option(S,K,sigma,r,T,optype):
'''计算欧式期权的Theta值
S 期权基础资产的价格
K 期权行权价
sigma 基础资产价格百分比变化的波动率
r 无风险收益率
T 期权合约剩余时间(年)
optype 期权类型;'call'看涨,'put'看跌
'''
d1 = (np.log(S/K) + (r + pow(sigma,2)/2)*T) / (sigma*np.sqrt(T))
d2 = d1 - sigma*np.sqrt(T)
theta_call = -(S*sigma*np.exp(-pow(d1,2)/2)) / (2*np.sqrt(2*np.pi*T)) - r*K*np.exp(-r*T)*norm.cdf(d2)
if optype=='call':
theta = theta_call
else:
theta = theta_call + r*K*np.exp(-r*T)
return theta
还是以例1的股票为例子,计算其Theta值
theta_option(S=5, K=6, sigma=0.24, r=0.04, T=0.5, optype='call')
# 输出
>>> -0.2665440940041926
# 日历天Theta
theta_option(S=5, K=6, sigma=0.24, r=0.04, T=0.5, optype='call') / 365
# 交易日Theta
theta_option(S=5, K=6, sigma=0.24, r=0.04, T=0.5, optype='call') / 252
需要注意的是,在布莱克-斯科尔斯默顿模型中,时间是以年为单位的。但是,在计算Thea时, 时间则是以天为单位。因此 Theta表示了在其他变量不变的情况下,过了1天以后期权价值的变化。
在实践中,可以计算“每日历天”的 Theta或“每交易目”的 Theta。其中,“每日历天”的 Theta就是计算以日历天数衡量的 Theta,计算 Theta的公式必须除以365。“每交易日”的 Theta则是计算以交易日天数衡量的 Theta,计算 Theta的公式则是除以252,一般一年的交易日天数通常是252天
基础资产价格与Theta的关系
用例1股票为例,观察股票价格与Theta的关系
S_list = np.linspace(4.0, 8.0, 100)
theta_list1 = theta_option(S_list, K=6, sigma=0.24, r=0.04, T=0.5, optype='call')
theta_list2 = theta_option(S_list, K=6, sigma=0.24, r=0.04, T=0.5, optype='put')
plt.figure(figsize=(8,6))
plt.plot(S_list, theta_list1, 'b-', label='看涨期权', lw=2.5)
plt.plot(S_list, theta_list2, 'r-', label='看跌期权', lw=2.5)
plt.xlabel('股票价格', fontsize=13)
plt.ylabel('Theta', fontsize=13, rotation=90)
plt.xticks(fontsize=13)
plt.yticks(fontsize=13)
# plt.ylim(-1.0, 1.0)
plt.title('股票价格与期权Theta的关系', fontsize=14)
plt.legend(fontsize=13)
plt.grid('True');
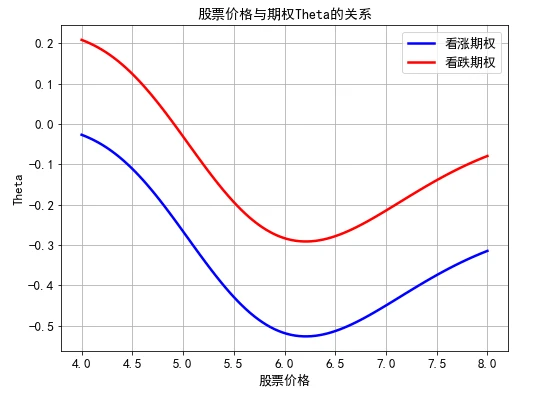
上图显示了看涨、看跌股票期权的 Theta与基础资产价格之间关系的曲线。从图中可以得到如下4个结论:第一,无论是看涨期权还是看跌期权, Theta与基础资产价格之间关系的曲线形状是很相似的;第二,在期权行权价格(6元/股)附近,也就是接近于平价期权的时候,无论是看涨期权还是看跌期权, Theta是负值并且绝对值很大,这就意味着期权的价值对时间的变化非常敏感;第三,当基础资产价格大于执行价格时, Theta的绝对值处于下降阶段;第四,当基础资产价格小于执行价格时,对于看跌期权而言,随着基础资产价格不断减小,期权 Theta将由负转正并趋近于某一个正数,而看涨期权的 Theta则趋近于零。
期权期限与Theta的关系
仍用例1股票为例,观察期权期限与Theta的关系
T_list = np.linspace(0.1, 5.0, 100)
theta1 = theta_option(S=7, K=6, sigma=0.24, r=0.04, T=T_list, optype='call')
theta2 = theta_option(S=6, K=6, sigma=0.24, r=0.04, T=T_list, optype='call')
theta3 = theta_option(S=5, K=6, sigma=0.24, r=0.04, T=T_list, optype='call')
plt.figure(figsize=(8,6))
plt.plot(T_list, theta1, 'b-', label='实值看涨期权多头', lw=2.5)
plt.plot(T_list, theta2, 'r-', label='平价看涨期权多头', lw=2.5)
plt.plot(T_list, theta3, 'g-', label='虚值看涨期权多头', lw=2.5)
plt.xlabel('期权期限', fontsize=13)
plt.ylabel('Theta', fontsize=13, rotation=90)
plt.xticks(fontsize=13)
plt.yticks(fontsize=13)
plt.title('期权期限与期权Theta的关系', fontsize=14)
plt.legend(fontsize=13)
plt.grid('True');
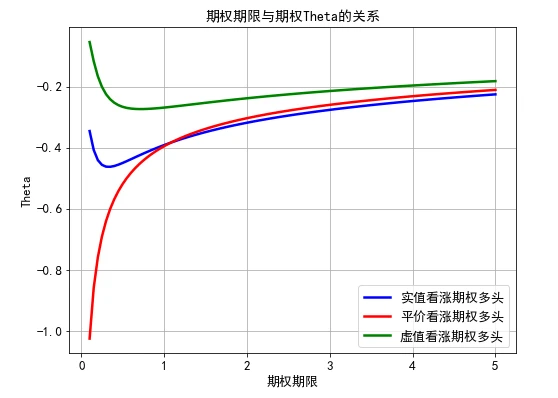
上图显示了实值看涨期权、平价看涨期权、虚值看涨期权的 Theta随期权期限变化的规律。图中有3条曲线,从上往下依次是虚值、实值以及平价期权。从图中可以得到以下3个结论:一是当期权期限越短(即越临近期权到期日),平价期权的Thea绝对值越大,并且与实值期权、虚值期权在Thea上的差异也是最大的。对此,可以利用直觉来理解这一点,因为当期权是平价时,期权到期时行权的不确定性最大,所以平价期权的价值对时间的敏感性就很大;二是平价期权的Thea值是期权期限的递增函数,相反,虚值期权和实值期权的 Theta值在期权期限较短时是期限的递减函数,在期限较长时则是期限的递增函数;三是当期权期限不断变长时,实值期权、平价期权、虚值期权的 Theta将会趋近。
前文链接????
1、期权类型与到期盈亏(投资必知必会)
2、定价模型与平价关系式(投资必知必会)
3、期权价格和相关变量的关系(投资必知必会)

