题目描述

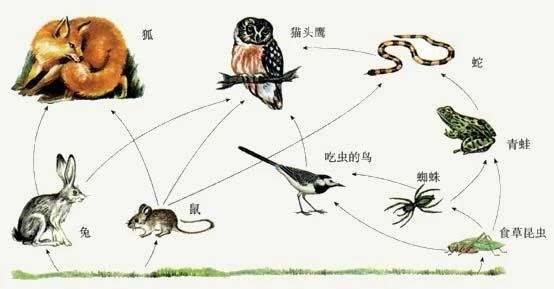
如图所示为某生态系统的食物网示意图，据图回答此题。

现在给你 n n 个物种和 m m 条能量流动关系，求其中的食物链条数。

物种的名称为从 1 1 到 n n 的编号。

m m 条能量流动关系形如

a1 b1 a2 b2 a3 b3 … … am−1 bm−1 am bm  a 1   b 1   a 2   b 2   a 3   b 3   …   …   a m − 1   b m − 1   a m   b m  

其中 ai bi a i   b i 表示能量从物种 ai a i 流向物种 bi b i 。注意单独的一种孤立生物不算一条食物链。

输入格式

第一行两个整数 n n 和 m m ,接下来 m m 行每行两个整数 ai bi a i   b i 描述 m m 条能量流动关系。

（保证输入数据符合生物学特点，且不会有重复的能量流动关系出现）

输出格式

一个整数，即食物网中的食物链条数。

样例输入

10 16
1 2
1 4
1 10
2 3
2 5
4 3
4 5
4 8
6 5
7 6
7 9
8 5
9 8
10 6
10 7
10 9

样例输出

9

思路

首先记录每个点的入度个数和出度个数。

那么，入度为0的点一定是生产者,定义 f[i] f [ i ] 为当前点的食物链的条数，那么对于生产者 f[i]=1 f [ i ] = 1 ,然后进行bfs,把生产者加入队列然后把走到的点的食物链条数更新成自己和走到的点的条数总和,再把走到的点的入度-1，最后统计一下出度为0且有入度的 f[i] f [ i ] 总和即为答案

代码

#include <cstdio>
#include <cstring>
#include <cctype>
#include <stdlib.h>
#include <string>
#include <map>
#include <iostream>
#include <sstream>
#include <set>
#include <stack>
#include <cmath>
#include <queue>
#include <vector>
#include <algorithm>
#include <list>
using namespace std;
#define mem(a, b) memset(a, b, sizeof(a))
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1
#define rson m + 1, r, rt << 1 | 1
#define inf 0x3f3f3f3f
typedef long long ll;
const int N = 100000 + 10;
const int M = 200000 + 10;
int n, m;
int first[N], tot;
int in[N], vis[N], out[N], f[N], in2[N];
struct node
{
    int v, next;
} e[M];
void add_edge(int u, int v)
{
    e[tot].v = v;
    e[tot].next = first[u];
    first[u] = tot++;
}
void init()
{
    mem(first, -1);
    mem(in, 0);
    mem(out, 0);
    mem(f, 0);
    mem(vis, 0);
    mem(in2, 0);
    tot = 0;
}
int bfs()
{
    queue<int> q;
    for (int i = 1; i <= n; i++)
    {
        if (!in[i])
        {
            f[i] = 1;
            q.push(i);
        }
    }
    while (!q.empty())
    {
        int u = q.front();
        q.pop();
        for (int i = first[u]; ~i; i = e[i].next)
        {
            int v = e[i].v;
            f[v] += f[u];
            in[v]--;
            if (!in[v])
                q.push(v);
        }
    }
}
int main()
{
    //freopen("in.txt", "r", stdin);
    int u, v;
    scanf("%d%d", &n, &m);
    init();
    for (int i = 1; i <= m; i++)
    {
        scanf("%d%d", &u, &v);
        add_edge(u, v);
        in[v]++;
        in2[v]++;
        out[u]++;
    }
    int ans = 0;
    bfs();
    for (int i = 1; i <= n; i++)
    {
        if (!out[i] && in2[i])
            ans += f[i];
    }
    printf("%d\n", ans);
    return 0;
}