数学建模分类问题模型

引言

2023MathorcupD题是一道数据分析问题，但是在最后一问中却有了本来应该是动力学模型的仿真问题，对于数据在缺少物理公式的情况下做仿真的确是个棘手的问题。思考再三，笔者在本题中所使用的方法为聚类分析筛选异常值点。计算软件为Python。感觉做法还是存在很多问题，模型还是有很多漏洞。望读者大佬们提出建议，共同进步。

问题背景

数据类型如下图所示：

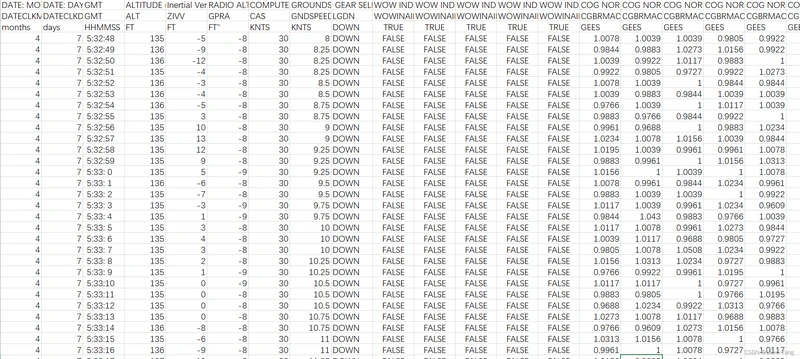
具体思路

由于本人不是航空航天专业，不知道在飞机飞行中什么样的数据参数算是异常，通过观察题中所给参数也无法通过作图直观反映出异常值点。因此，笔者另辟蹊径，用数据本身说话，让数据自己判断谁是异常值点（当然判断出来的是可能的异常值点，就好像犯罪嫌疑人只是大概率是罪犯，但也并不一定是罪犯）。通过对数据进行K-means聚类（其他类型的聚类模型也可以，对大致结果影响不大），先对数据进行区域划分。由于QAR数据本质上是时间序列型数据，从时间这个维度上讲其变化量应该是近似连续的，相同的飞行阶段很容易归为一类。因此理论上各个飞行阶段可以有很明显的类分界情况。这时候，我们要做的就是找到离群点，找出与最近的聚类中心偏离最大的点，我们便可锁定其为“犯罪嫌疑人”了，即异常值点。此时，通过统计学的方法，确定一个距离阈值，便可划分正常点和异常点了。当然，还没有结束。聚类模型没有办法得到一个准确的数学公式对异常值点进行划分，换言之，换一个数据集，情况又不同了。而且，倘若对于未来某种情况，没有大量数据作为支撑时，该方法便很难奏效。因此，我们还需要引入SVM支持向量机分类模型。将我们聚类后的结果用SVM进行分类训练，通过大量数据集的训练，对于特定飞机型号，SVM模型便可以给出异常值判断的超平面方程，从严谨的数学公式上对异常值点进行区分。这样，对于往后任意给出飞机的QAR参数，我们都可以之间判断其是否为异常值点了。模型便拥有了普适性（至少对于一种型号的飞机而言）。

当然该模型存在一些漏洞。首先，通过纯数据的方法分析物理仿真问题很不精确，就好像通过数据去拟合物理公式一样，不是很靠谱。（实在没办法也只能这样搞~~）其次，聚类是高纬数据，想要进行离群点筛选必须转换为一维数据，数据的维度压缩存在误差。其次，阈值的选取很难有一个科学化的公式（本人没有找到类似文献cry~）,因此在异常值确定上只能做到嫌疑人锁定，即通过统计学方法，根据异常点可能的比例去筛选异常点。最后，可能会存在异常点被分入其他聚类中的可能，这种异常点没有办法通过该方法探查出来。

具体实现过程

以下是Python的实现过程：

plus：附一篇聚类处理异常值问题的英文文献。

库的导入

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans

主成分降维

PCA降维，不多赘述。

## 主成分分析
scaler = StandardScaler()
scaler.fit(data)
data = scaler.transform(data)
pca = PCA(n_components=0.95)
pca.fit(data)
PCA_Data = pca.transform(data)
tzxl = pca.components_
tz = pca.explained_variance_
gxl = pca.explained_variance_ratio_
tzxl = pd.DataFrame(tzxl)
covar = pca.get_covariance()
tzxl.to_excel('特征向量1.xlsx')
pd.DataFrame(gxl).to_excel('各主成分重要性.xlsx')

K-means聚类

K-means聚类不多赘述，以下是聚类个数确定的公式：

## 聚类分析
def k_SSE(X, clusters):  ## 碎石过程
    X = pd.DataFrame(X)
    # 选择连续的K种不同的值
    K = range(1,clusters+1)
    # 构建空列表用于存储总的簇内离差平方和
    TSSE = []
    for k in K:
        # 用于存储各个簇内离差平方和
        SSE = []
        kmeans = KMeans(n_clusters=k)
        kmeans.fit(X)
        # 返回簇标签
        labels = kmeans.labels_
        # 返回簇中心
        centers = kmeans.cluster_centers_
        # 计算各簇样本的离差平方和，并保存到列表中
        for label in set(labels):
            SSE.append(np.sum((X.loc[labels == label,]-centers[label,:])**2))
        # 计算总的簇内离差平方和 
        TSSE.append(np.sum(SSE))

    # 中文和负号的正常显示
    plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
    plt.rcParams['axes.unicode_minus'] = False
    # 设置绘图风格
    plt.style.use('seaborn-white')
    # 绘制K的个数与GSSE的关系
    plt.figure(dpi=400,figsize=(12,8))
    plt.plot(K, TSSE, color='red',marker='d')
    plt.title('K_selection')
    plt.xlabel('number_of_cluster')
    plt.ylabel('the value of SSE')
    # 显示图形
    plt.show()
    
cluster_data = PCA_Data
k_SSE(cluster_data, 15)  # 求出k值
cluster_data = pd.DataFrame(cluster_data)

离群点计算

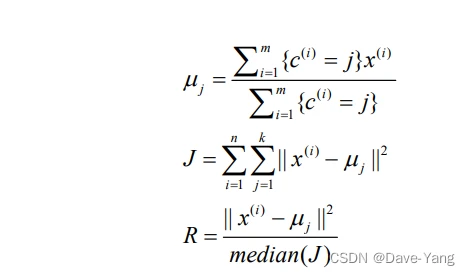
cluster_data = PCA_Data
k_SSE(cluster_data, 15)  # 求出k值
cluster_data = pd.DataFrame(cluster_data)

k = 2
threshold = 20  # 阈值选择3
model = KMeans(n_clusters = k, max_iter = 500)  # 分为k类
model.fit(cluster_data)  # 开始聚类
cluster_data['label'] = model.labels_ # 将聚类后的类别标签生成label列
relative_distance = []
for i in range(k):  # 逐一处理
    rank = range(len(cluster_data.columns)-1)
    distance = cluster_data.query("label == @i")[rank] - model.cluster_centers_[i]  # 计算各点至簇中心点的距离
    absolute_distance = distance.apply(np.linalg.norm, axis = 1)  # 求出绝对距离
    relative_distance.append(absolute_distance / absolute_distance.median())  # 求相对距离并添加
    
cluster_data['relative_distance'] = pd.concat(relative_distance)  # 合并
cluster_data['outlier_3'] = cluster_data.relative_distance.apply(lambda x: 1 if x > threshold else 0)
cluster_data['outlier_3'].value_counts()
cluster_data[['relative_distance','outlier_3']].to_excel('data8_unusual.xlsx')

可视化结果

# 绘图查看离群点的相对距离
fig, ax = plt.subplots(figsize=(10,6))
colors = {0:'blue', 1:'red'}
ax.scatter(cluster_data.index, cluster_data.relative_distance, c=cluster_data.outlier_3.apply(lambda x: colors[x]))
ax.set_xlabel('仿真时间')
ax.set_ylabel('相对距离')
plt.show()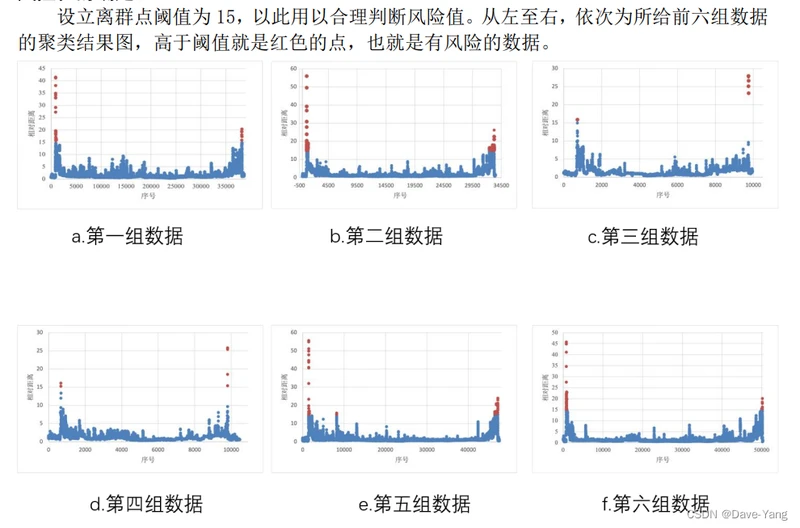

SVM数据集训练

## SVM分类训练
x = train_data.iloc[:,0:20]
x = x.fillna(0)
y = train_data['outlier_3']
y = y.fillna(1)
x.to_excel('input.xlsx')
y.to_excel('output.xlsx')
clf = svm.SVC(kernel='sigmoid',C=0.9)
clf.fit(x,y)
data = pd.read_pickle('data1.pkl')
sns.boxplot(data = data.iloc[:,[4]])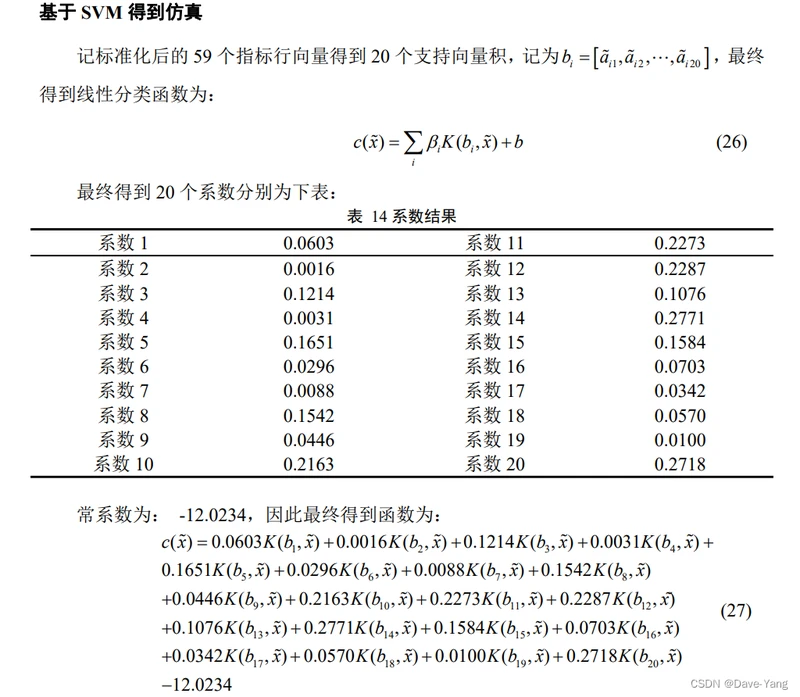

结语

这次比赛得了二等奖，很开心，谨以此纪念我的mathorcup比赛经历。QAQ

引言