💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
2.1 干涉和衍射的交互式仿真
2.2 衍射光栅光谱
2.3 一阶衍射的扩展视图
2.4 用白光照射的衍射光栅
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
-
衍射光栅是一种具有周期性结构的光学元件,它通过衍射现象来分散和操控光束。衍射光栅通常由一系列平行的凹槽或凸起构成,这些结构按照一定的周期排列。当入射光束通过衍射光栅时,光波会在光栅的结构上发生衍射,形成一系列的衍射波。这些衍射波会按照一定的角度和强度分布进行偏折和干涉,从而实现光的分散和操控。
衍射光栅的性质和效果主要取决于光栅的周期和结构参数,以及入射光的波长。其中,最重要的参数是光栅的周期,即凹槽或凸起之间的间距。光栅的周期决定了衍射光栅的分散能力,即能够将入射光束分散成不同波长的光束。此外,光栅的结构参数,如凹槽或凸起的形状、深度等,也会影响衍射光栅的性能。
衍射光栅的应用非常广泛。其中,最常见的应用是光谱学领域。衍射光栅可以用于分散入射光束,将不同波长的光分离出来,从而实现光谱分析。此外,衍射光栅还可以用于光学显微镜、激光器、光通信等领域,用于光束的操控、波前调制等应用。
总之,衍射光栅是一种通过衍射现象来分散和操控光束的光学元件。它具有广泛的应用,特别是在光谱学和光学操控领域中发挥着重要作用。
📚2 运行结果
2.1 干涉和衍射的交互式仿真
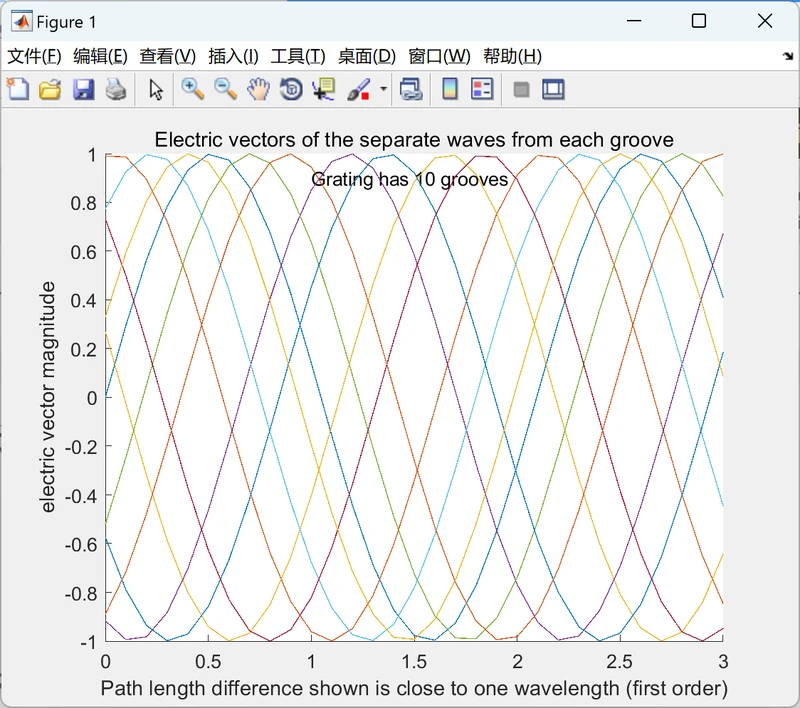
模拟反射之间的干扰 衍射光栅中的相邻凹槽,显示了如何操作 衍射光栅通过添加一堆 正弦波。带有N槽的光栅是 由纯单色光照射。当从某个角度观看时, 来自每个凹槽的反射在略有不同的路径上传播 长度,因此相对于每个略有相移 其他。在此模拟中,来自每个反射的光束为 由其电磁矢量的正弦波表示。每 反射略有相移 与相邻反射相比,其量取决于 波长和相邻路径长度的差异 思考。当所有正弦波相加时,这种相移 导致部分消除某些波,称为干扰。作为路径 长度差异被改变(通过按左右光标箭头键),出现衍射图案 每当路径长度差为 波长的整数数(称为“阶数”),从而得到 在建设性的干扰中。随着凹槽数量 N 的增加(通过按向上和向下光标箭头键), 这些最大值变得非常尖锐,最大值之间的强度 变得越来越低。真正的光栅有数千个凹槽,因此具有极其尖锐的最大值,几乎完全 千里马之间的黑暗。最大值是不同的顺序” 的衍射。观看“总强度...”下面报告 接近路径长度差异时的正弦波图,该差异为 波长的整数。从 2 个凹槽开始,然后 逐渐增加以查看衍射图案如何演变。
2.2 衍射光栅光谱
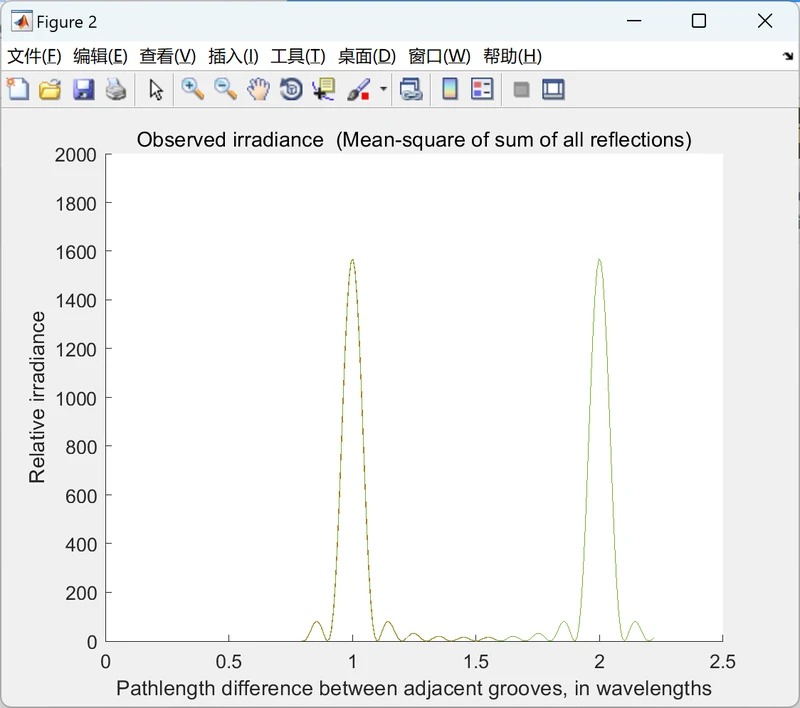
衍射光栅光谱照明的自运行模拟 通过单色光。显示了总强度的图,在 探测器与入射光的波长(在路径上表示 相邻反射之间的长度差,PLD)。这是有启发性的 运行此模拟时,凹槽数 N=2,然后 N=3,N=4, 等等。每当路径长度出现强度的最大值时 差值 (PLD) 是波长的整数(称为 “订单”)。随着凹槽数量越来越大,最大值 变得非常尖锐,最大值之间的强度几乎为零。 在此图中,凹槽 N 的数量为 100。
2.3 一阶衍射的扩展视图
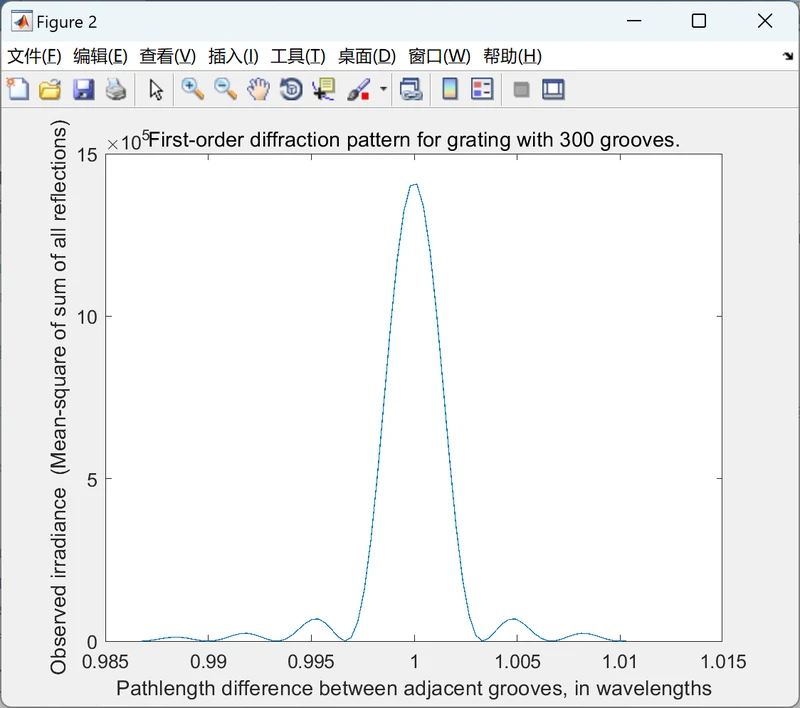
光栅的一阶衍射图谱特写 单色光。显示由有限引起的“衍射极限” 凹槽数量,N。N 越大,此模式越窄,并且 更高的光栅衍射极限分辨率。宽度 最大值与凹槽数量 N 成反比。在 这个数字,凹槽N的数量是300。真实实用 光谱仪无法实现这种所谓的衍射极限 分辨率,因为它必须利用有限的狭缝宽度才能 允许足够的光线进入探测器。作为狭缝与 接近零,有效分辨率接近衍射 此处说明的极限,但到达 检测器接近零。
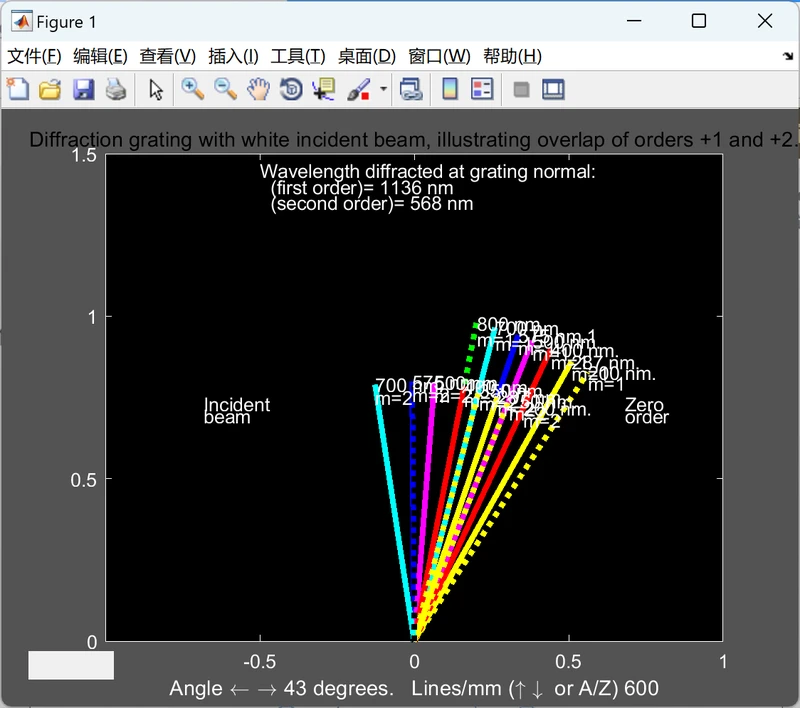
2.4 用白光照射的衍射光栅
部分代码:
for j=1:N,
y=sin(3.*x+a);
z=z+y; % z is waveform (sine) resulting from superimposition
a=a+pld;
end
intensity(k)=sum(z.*z); % calculates mean amplitude
OPL(k)=pld./(2*pi);
plot(OPL(1:k-1),intensity(1:k-1))
ylabel('Observed irradiance (Mean-square of sum of all reflections)')
xlabel('Pathlength difference between adjacent grooves, in wavelengths')
title(['First-order diffraction pattern for grating with ' num2str(N) ' grooves.'])
%drawnow
k=k+1;
end
hold off
figure(2)
ElapsedTime=cputime-start
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
-
陈光炜, 陈光炜. 光学与光谱学[M]. 科学出版社, 2014.
-
王光辉, 王光辉. 光学[M]. 高等教育出版社, 2017.
-
李大鹏, 李大鹏. 光学[M]. 高等教育出版社, 2016.
-
陈光炜, 陈光炜. 光学与光谱学实验指导[M]. 科学出版社, 2015.

