没有开场白,直接上正文。
emmm还是先做一个一元函数微分的回顾。
回顾
Notes
- y=f(x)在x=x0处可微;y=f(x)在x=x0处可导,二者互为充要条件
- A=f’(x0)
- y=f(x)可导,则dy=f’(x)dx即df(x)=f’(x)dx
二元函数全微分定义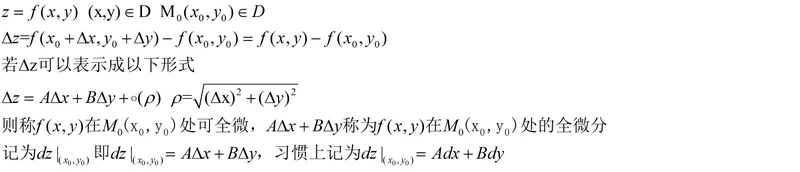
Notes
比对一元函数的微分,分析二元函数的微分,
1.从增量部分来看,相对于一元函数微分,二元函数有两个自变量,所以全微分的增量就需要用到全增量;
2.从微分部分来看,一元函数微分的表示形式为Adx,二元函数的全微分表示形式则需要将全增量全部表示出来,即Adx+Bdy
3. 从高阶无穷小部分来看,一元函数微分只需要考虑增量Δx即可,二元函数则需要兼顾Δx和Δy
结论(重点)
定理一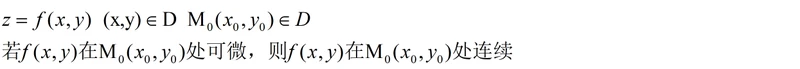
证明
定理二
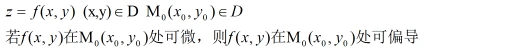
证明

关于证明步骤中Δy或Δx取0的说明:
所谓二元函数全微分,就是关于二元函数全增量的微分,包含两个增量即可,至于增量取值可自行决定
例题
例1

例2
先算到这里,做一个重要的补充
根据可微的定义
有了上面的结论,继续做题
定理三
可微的充分条件(不一定必要)
若函数f(x,y)连续可偏导(连续可偏导的意思是偏导数fx’(x,y)和fy’(x,y)也是连续的,不是函数既连续又可偏导),则f(x,y)可微
函数f(x,y)关于x的一阶偏导数fx’(x,y)和关于y的一阶偏导数fy’(x,y)连续,证明函数f(x,y)可微

总结
本篇需要总结的东西还是比较多的,分两部分吧
1.在函数可偏导的情况下判断函数是否可微
2 函数连续、可偏导、可微和连续偏导的关系
- 最强的条件——连续偏导
- 如果函数连续偏导,则函数可微
- 如果函数可微,则函数连续,函数可偏导
反之,
- 如果函数连续,未必可微
- 如果函数可偏导,未必可微
