本文主要探讨PID算法在使用时的一些实际问题、处理技巧和方法,学习本节内容需要先对PID控制算法有基本的了解。
1)PID控制的基本原理
PID是一个二阶线性控制器,它具有不需要建立数学模型,控制效果好,良好的鲁棒性等等优点。
它的原理如下图:
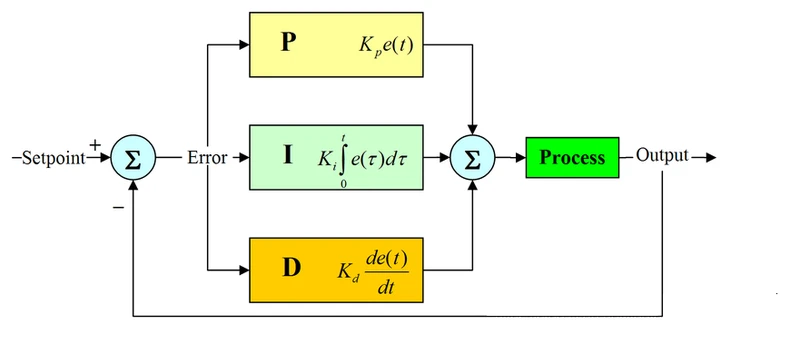
PID的基本定义公式如下:
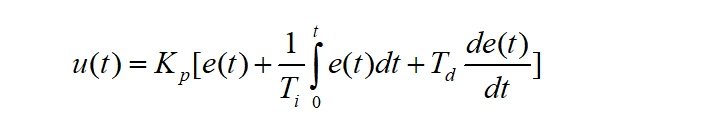
其中u(t)是控制器的输出;
e(t)是控制器的输入,一般是设定值与控制值的差,即e(t) = r(t) - c(t);
Kp、Ti、Td分别是比例、积分、微分系数。
PID是对输入偏差进行比例(P)、积分(I)、微分(D)运算,将结果叠加,去控制执行机构。通过调节比例、微分、积分的系数,使得控制系统达到良好的闭环控制性能。实际中使用PID调节控制系统的输出,主要难点是进行PID的参数确定,这要根据实际情况进行调节。
2)离散形式的PID公式
一般的系统应用中,是使用离散形式的PID进行计算。将积分换为求和,微分换为差分,就可以得到离散形式的PID公式:
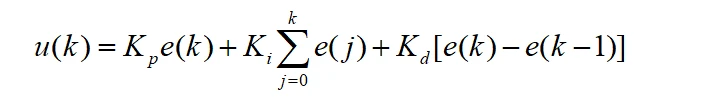
这里的u(k)就是输出,直接对应执行机构的输出值。
3)增量式PID控制
在上面的PID公式中,公式的输出u(k)直接对应于执行机构的输出值,称为位置式PID算法。
位置式PID算法有一定的缺点:一是计算量大,需要对e(k)进行累加;二是如果意外出现计算错误,会使执行机构出现大幅度动作,容易发生危险。
所以有了增量式PID的出现,增量式PID每次输出值是对应于本次执行机构位置的增量,而不是对应执行机构的实际位置,它的计算如下:
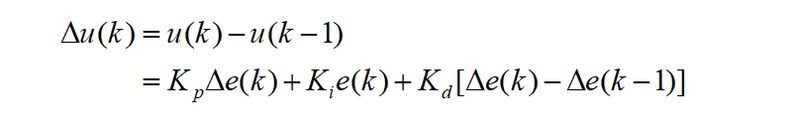
其中:Δe(k) = e(k) - e(k-1)。
一般计算机控制系统的采样周期T是不变的,所以,一旦确定了参数和前三次的测量值,就可以利用上式计算出后续的控制增量。增量式PID解决了位置式PID的一些缺点,一般在工程上编程实现时,往往都是采用的增量式PID。
4)PID的积分饱和及处理方法
在实际控制系统中,控制量的输出值是受执行机构性能的限制的,(比如阀门打开的程度,开到最大就不能再大了),而可能PID计算的输出要求更大,这时实际执行机构的控制量就不再是PID的计算值,这种情况就是饱和效应。
如果负载突变,引起误差的跳变,那么很容易出现饱和效应,此时,误差e(k)将会在很长一段时间内保持正值,而且值比较大,会使得累加后积分项非常大,当到达误差为0的情况时,积分项不能很快归0 ,而出现严重的超调现象。这是由于积分项引起的,所以叫积分饱和。
常用的抗饱和方法有积分分离法、遇限削弱积分法以及变速积分法等等。下面分别介绍这几种处理积分饱和的方法:
a)积分分离法
积分分离法的基本思路是当被调量与设定值偏差较大时,取消积分作用,以免积分作用使得后期超调量太大;当被控量接近给定值时,重新引入积分控制。
具体方法是依据实际情况人为设定一个阈值ε>0;当e(k)的绝对值大于ε时,取消积分项,采用PD控制;当e(k)绝对值小于等于ε时,使用通常的PID控制。用公式表达如下:
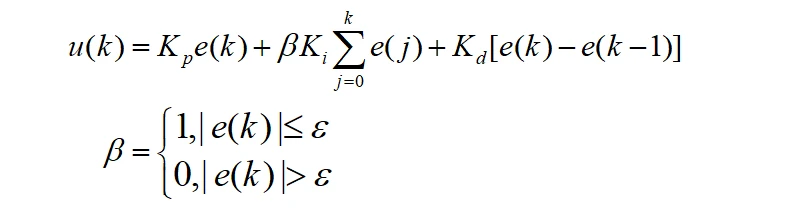
在实现时,实际上是e(k)的绝对值大于ε时,计算方法同3)增量式PID;当e(k)绝对值小于等于ε时,对应于增量式PID中即去掉含Ki的项:
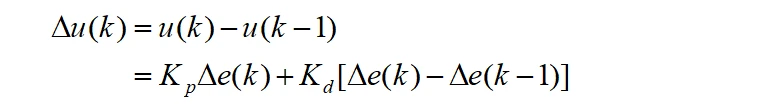
b)遇限削弱积分法
遇限削弱积分法,实现方法是,当控制量进入饱和区时,便不再进行积分项累加,而只执行削弱积分的运算;在计算u(k)时,先判断u(k-1)是否已经超出最大的控制量,如果已经有u(k-1) > Umax,则只累加负偏差;如果已经有u(k-1) < Umin,则只累加正偏差。
使用遇限削弱积分法,可以使得控制量u(k)的计算值不会偏离实际能控制的量太远,这样当需要反向调节时能较快地响应,避免输出长时间停留在饱和区,不会产生过多的超调量。
c)变速积分法
变速积分法,主要思想是,改变积分项的累加速度:当误差值e(k)绝对值很大时,减慢积分速度;当误差值e(k)绝对值很小时,加快积分速度。
这个方法相当于a)积分分离法的强化版;积分分离法在误差较大时,直接去除了积分量,误差较小时才引入积分量,属于有和无的变化;而变速积分法,对积分量的调节要缓和一些。
至于加快和减慢由何种方法实现,可以由用户自己定义,最简单的方法就是构造一个随e(k)负相关变化的函数f(e(k))作为系数,在计算积分量时,用e(k)*f(e(k))来代替e(k)累加。
欢迎大家关注我的公众号,更多学习资源分享:

