神经网络,也称为人工神经网络 (ANN) 或模拟神经网络 (SNN),是机器学习的子集,并且是深度学习算法的核心。其名称和结构是受人类大脑的启发,模仿了生物神经元信号相互传递的方式。
一、神经元的组成
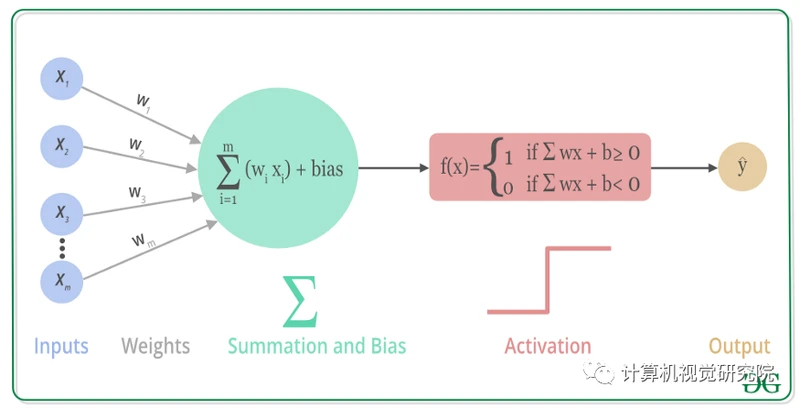
每个神经元包含wx+b的运算和一个激活函数组成。
将各个节点想象成其自身的线性回归模型,由输入数据、权重、偏差(或阈值)和输出组成。公式大概是这样的:
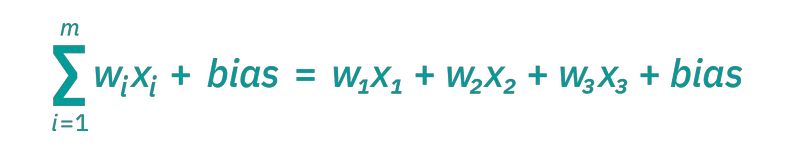
∑wixi + bias = w1x1 + w2x2 + w3x3 + bias
一旦确定了输入层,就会分配权重W。 这些权重有助于确定任何给定变量的重要性,与其他输入相比,较大的权重对输出的贡献更大。 将所有输入乘以其各自的权重,然后求和。 之后,输出通过一个激活函数传递,该函数决定了输出结果。
如下:是具有两个神经元的计算过程
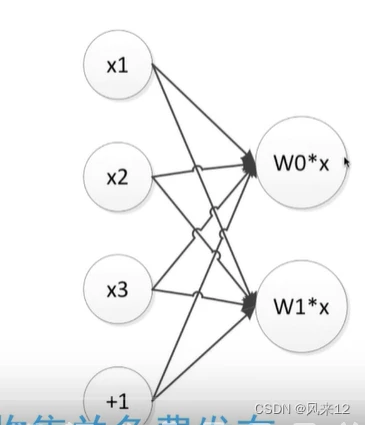

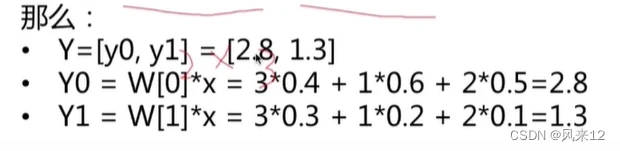
二、激活函数
激活函数(Activation Function)是一种添加到人工神经网络中的函数,旨在帮助网络学习数据中的复杂模式。类似于人类大脑中基于神经元的模型,激活函数最终决定了要发射给下一个神经元的内容。
1.Sigmoid 激活函数
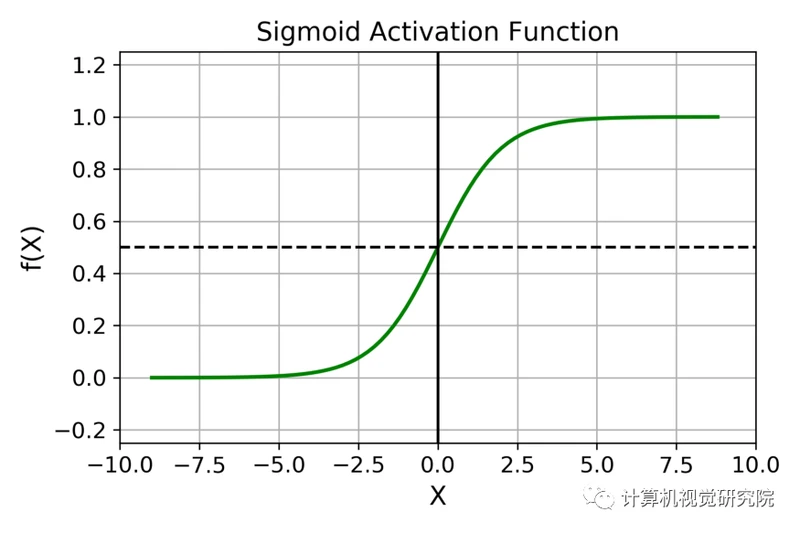
Sigmoid 函数的图像看起来像一个 S 形曲线。
函数表达式如下:
![]()
在什么情况下适合使用 Sigmoid 激活函数呢?
Sigmoid 函数的输出范围是 0 到 1。由于输出值限定在 0 到 1,因此它对每个神经元的输出进行了归一化;
用于将预测概率作为输出的模型。由于概率的取值范围是 0 到 1,因此 Sigmoid 函数非常合适;
梯度平滑,避免「跳跃」的输出值;
函数是可微的。这意味着可以找到任意两个点的 sigmoid 曲线的斜率;
明确的预测,即非常接近 1 或 0。
Sigmoid 激活函数有哪些缺点?
倾向于梯度消失;
函数输出不是以 0 为中心的,这会降低权重更新的效率;
Sigmoid 函数执行指数运算,计算机运行得较慢。
2. Tanh / 双曲正切激活函数
3. ReLU 激活函数
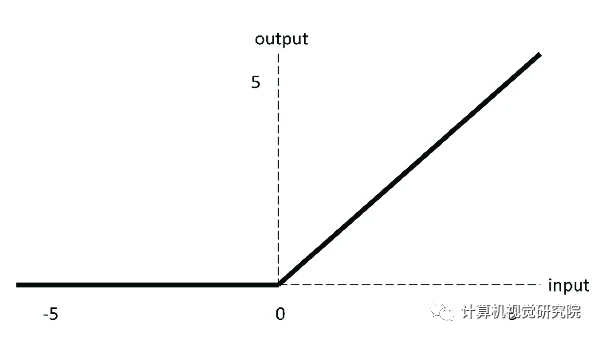
ReLU 激活函数图像如上图所示,函数表达式如下:
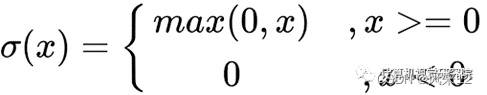
ReLU 函数是深度学习中较为流行的一种激活函数,相比于 sigmoid 函数和 tanh 函数,它具有如下优点:
当输入为正时,不存在梯度饱和问题。
计算速度快得多。ReLU 函数中只存在线性关系,因此它的计算速度比 sigmoid 和 tanh 更快。
4. Leaky ReLU
5. ELU

6. Softmax
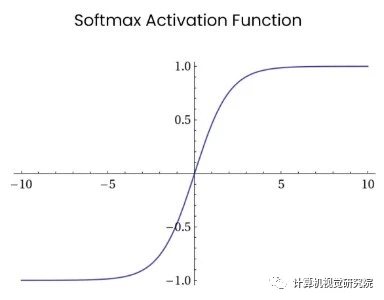
三、损失函数
影响神经网络训练的因素有很多,比如Loss函数,网络结构,参数优化,训练时间等,本节我们主要对loss函数进行介绍,损失函数可以表示为 L(y,f(x)) ,用以衡量真实值 y和预测值 f(x)之间不一致的程度,一般越小越好。为了便于不同损失函数的比较,常将其表示为单变量的函数,在回归问题中这个变量为 [y−f(x)] ,残差;在分类问题中为 [yf(x)] 趋势一致。
回归问题
(1)MSE 均方误差
均方误差(MSE)是回归损失函数中最常用的误差,也常被称为L2 loss,它是预测值与目标值之间差值的平方和,其公式如下所示:
![]()
优点:各点都连续光滑,方便求导,具有较为稳定的解。
缺点:不是特别的稳健,因为当函数的输入值距离中心值较远的时候,使用梯度下降法求解的时候梯度很大,可能导致梯度爆炸。
(2)平均绝对误差
平均绝对误差(MAE)是另一种常用的回归损失函数,也常被称为L1 loss,它是目标值与预测值之差绝对值的和,表示了预测值的平均误差幅度,而不需要考虑误差的方向,范围是0到∞,其公式如下所示:
![]()
分类问题
(1)0-1损失函数
以二分类问题为例,错误率=1-正确率,也就是0-1损失函数,可以定义为
(2) 绝对值损失函数
L(Y,f(X)=|Y−f(X)|
(3) Softmax Loss
对于多分类问题,也可以使用Softmax Loss。
机器学习模型的 Softmax 层,正确类别对于的输出是:
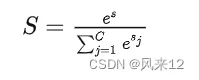
二分类问题用 One Hot Label + Cross Entropy Loss 或者Logistic loss
多分类问题用softmax, 它是sigmoid函数在多分类问题上的推广。
四、根据梯度计算出使损失函数最小的W值
梯度是神经网络里绕不开的一个概念。
一句话:梯度是一个向量,用来指明在函数的某一点,沿着哪个方向函数值上升最快,这个向量的模指明函数值上升程度(速度)的大小。
接下来举例
本质上,梯度就是一个向量,如果函数是n元函数,这个向量就是由n个元素组成。如果是二元函数,
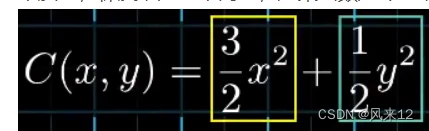
这个向量就是:
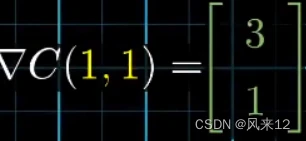
计算方式为求偏导,然后带入点值。
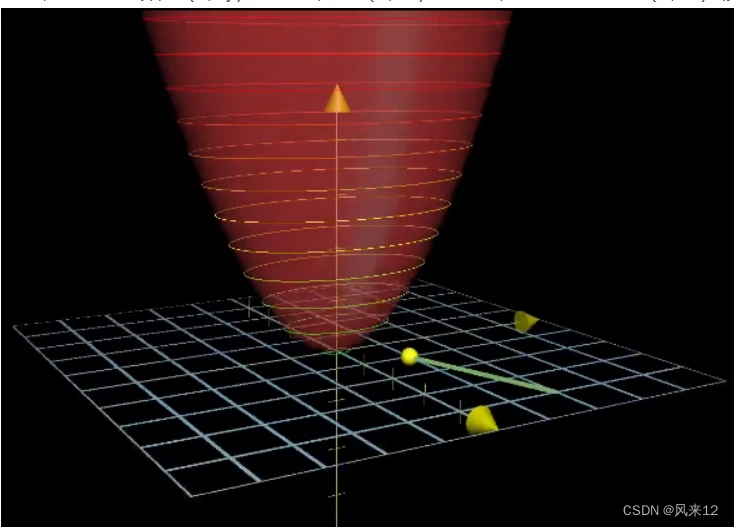
可以得到在(1,1)这一点,沿着方向(3,1)函数值上升速度最快。
如图,红色是函数C(x,y)的图像,在(1,1)这一点,可以看到沿着(3,1)移动,函数值(Z轴)是上升最快的。
在神经网络中,我们经常要找一个函数的最小值,这个函数即损失(loss)关于网络中各个参数(parameter)的权重的函数。
如果我们算出这个函数的梯度,我们就知道对每一个参数,如何设置能够使损失上升最快。
那么我们减去这个梯度(即参数vector减去梯度vector),就能使损失下降最快了。
再加一个学习率,就能控制这个下降速度了。
