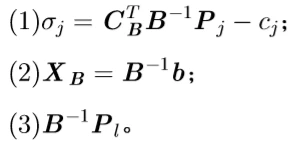单纯形法
现在假设原线性规划中,不存在单位矩阵
I
I
I,所取的基是一般形式的
B
B
B,则形式如下:
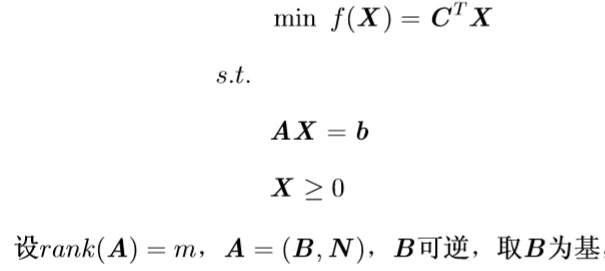
①最优解判别准则(如何判断我们得到的解是否是最优解,然后终止迭代):
判别数和基都一般化时的情况:
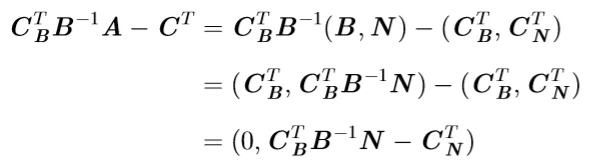
若令
σ
j
=
C
B
T
B
−
1
P
j
−
c
j
\sigma_j=C^T_BB^{-1}P_j - c_j
σj=CBTB−1Pj−cj,
j
=
1
,
…
,
n
j = 1,\dots,n
j=1,…,n,则当任意
σ
j
≤
0
\sigma_j\leq 0
σj≤0时,
X
=
(
B
−
1
b
,
0
)
X = (B^{-1}b,0)
X=(B−1b,0)为最优解
②换基操作:如果当前顶点不是最优解时,如何从一个基可行解(顶点)沿下降方向到另一个基可行解(顶点)
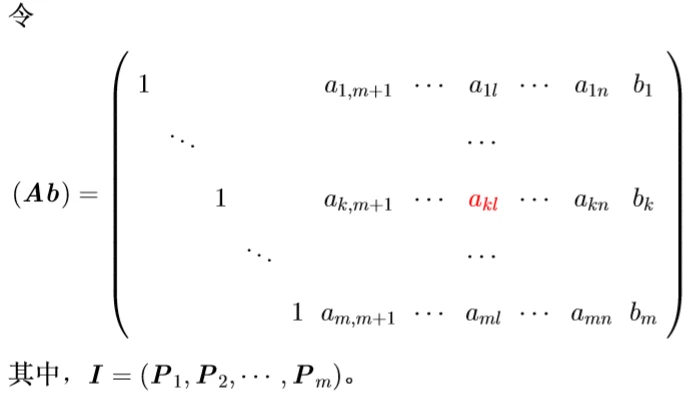
设第
l
l
l列是进基列,第
k
k
k列是出基列,
a
k
l
a_{kl}
akl是主元,即
σ
l
>
0
\sigma_l >0
σl>0,
a
k
l
>
0
a_{kl} > 0
akl>0,则我们的目标是将
P
l
P_l
Pl通过行初等变换变成单位向量,此时
P
k
P_k
Pk变成非单位向量,如下:

行初等变换规则(分为系数和增广系数)如下,不用死记硬背:
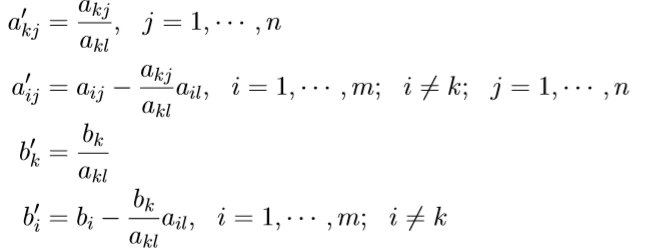
主元的选择方法:
首先,主元必须大于0,不然进基后,增广系数会为负数,破坏标准线性规划形式;在同样大于0的情况下,要保证在行变换过程中所有增广系数都非负,因此满足下式成立:
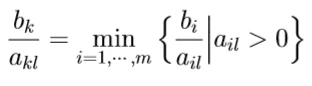
③进基列的选择:如何选择进基列可以使目标函数有较大的下降
- 基可行解
X
0
=
(
B
−
1
b
,
0
)
X^0=(B^{-1}b,0)
X0=(B−1b,0)非退化
若是退化的基可行解,则此时不同的基可能对应相同的解,因此是非严格下降的,该要求能保证严格递减 - 进基列的判别数
σ
j
>
0
\sigma_j >0
σj>0
σ j > 0 \sigma_j >0 σj>0说明以它为基,目标函数值还可以减小 - 进基列向量中至少有一个元素是正的
保证可以变小并且是有界的变小,而不是无穷小导致原线性规划无最优值
判别数:
σ
j
=
C
B
T
B
−
1
P
j
−
c
j
\sigma_j = C^T_BB^{-1}P_j-c_j
σj=CBTB−1Pj−cj
无解:判别数
σ
j
>
0
\sigma_j >0
σj>0,但是
P
j
<
0
P_j<0
Pj<0,此时无解
无穷多最优解:存在一个非基变量对应的判别数为0
唯一解:所有非基变量对应的判别数严格小于0
补充:计算单纯形表最后一行的小技巧
在进行换基运算时,可以同时对单纯行表最后一行做行初等变换(让进基列判别数为0),变换公式如下:
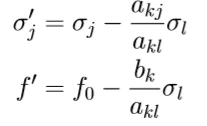
避免循环
当基可行解退化时,可能出现循环情况
解决方法:左上原则
进基列选择所有判别数为正的最左边的一列,主元选择(多个最小值)行标最小的
修正单纯形法(一般计算机编程实现用)
优点: 不需要画多个表格,只需要存储一个基矩阵的逆
思想: 用初等矩阵记录一系列的行初等变换的过程,只保留参与迭代的列向量的运算
新一轮迭代:
上一轮迭代变换后的进基列
P
j
k
−
1
=
B
k
−
1
−
1
P
j
0
P_j^{k-1} = B_{k-1}^{-1}P_j^0
Pjk−1=Bk−1−1Pj0
加入新进基列后的矩阵
M
M
M,强制转化成单位阵需要的初等矩阵
E
E
E,也就是求
M
M
M的逆
在上一轮基矩阵的逆的基础上,得到新一轮基矩阵的逆:
B
k
=
M
−
1
B
k
−
1
B_k = M^{-1}B_{k-1}
Bk=M−1Bk−1
计算新
b
b
b、新
σ
\sigma
σ
根据新
σ
\sigma
σ找出本轮的进基列,并计算本轮迭代变换后的进基列
P
j
k
=
B
k
−
1
P
j
0
P_j^{k} = B_{k}^{-1}P_j^0
Pjk=Bk−1Pj0
根据本轮迭代变换后的进基列和新
b
b
b,挑选主元进入下一轮迭代