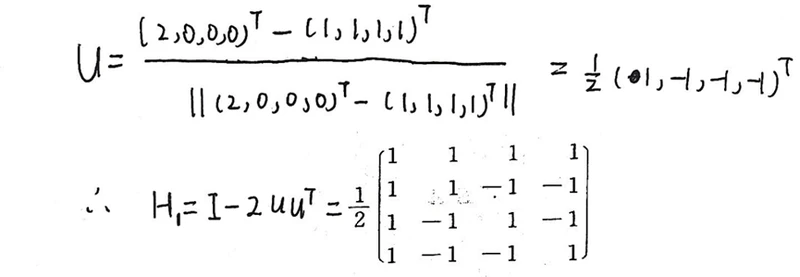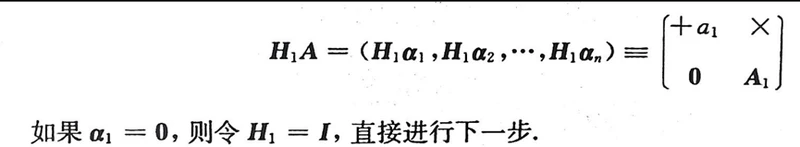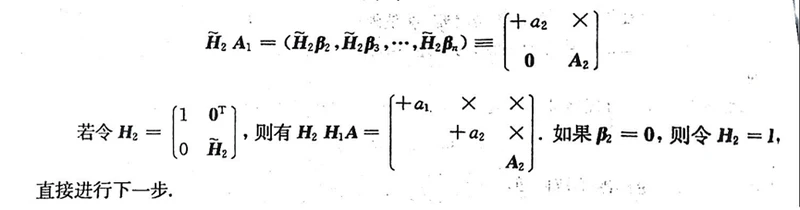参考书籍和图片来源:《矩阵分析与计算》李继根 张新发编著 第三章QR分解部分
QR分解的3种方法:
方法一:经典的Gram-Schmidt(CGS)算法(就是基于施密特正交化)
方法二:对CGS算法进行改进后的MGS(Modified Gram-Schmidt)算法(就是对施密特正交化算法进行了一点优化)
方法三:利用Householder变换法求QR分解
先复习一下施密特正交化:
公式如上,我稍微用言语解释一下,不懂的话参考其他资料,很简单的。
β 是一个正交的基,α 是在这个基张成的空间里的j个不相关的向量,施密特正交化的作用就是将j个α 变换为j个β 这个正交基。变换方法主要是向量分解,将α 分解为β 这个基下的n个分量,然后减去分量只留下一个方向的分量。
可以参考知乎文章怎么巧记施密特正交公式?如图。? - 知乎
好了我们知道施密特正交化后,我们直接来个一题三解,题目如下
我们先写方法一和方法二,因为它俩本质上都是施密特正交化,方法二只是在方法一的基础上的改良!

你仔细看一下步骤,就会发现,方法一和方法二的区别就在我在图片中圈出来的地方步骤的区别。
方法一(CGS算法)在求β 时,会不断迭代,不断减去和它正交的方向的分量,就像图中的第一个方框,β3需要减去β1和β2方向上的分量,那么是不是意味着随着向量的增多β 需要减去的分量会越来越多!所以CGS迭代算法在数值上是不稳定的!
而方法二(MGS算法)的想法是每当产生一个新的正交向量β 后,就重新计算后续所有向量α ,消去其中包含已产生的β 成分,从而使这些改变后的后续向量都与以及计算出来的β 正交。
你看图中的后面两个框,在求β2去掉β1方向上的分量的时候,是不是就把β3 在β1 上面的分量部分减掉了,所以后面求β3 的时候就只需要减去β2 方向上的分量就行了,这样就不会产生减法的累计,避免了数值上的不稳定!
也许你会说这根本不是QR分解好吧,其实我们将上面的运算写出来后,QR分解答案也就出来了。 A=QR,上面求出来的正交单位矩阵就是Q矩阵,我们又知道A矩阵,所以R=![]() A,R求出来后QR分解不就出来了嘛。
A,R求出来后QR分解不就出来了嘛。
下面介绍解法3,基于Householder变化的QR分解(我之前的笔记有讲Householder变换,忘记了可以去看看):
第一步:
用方程表示就是
至于H1的求法,就是把α1 这个向量投影到A这个空间对应的X轴上的Householder变换(不理解可以看后面的实例再回来理解一下这句话)
第二步:
就是对第一步求出来的
中的A1进行同样的操作,把A1的第一列投影到A1空间对应的X轴上(说白了就是要让Householder变换让A1的第一列只有第一个元素!!!),求得的Householder矩阵是为H2。用公式表示就是
步骤说完了:我们直接来做题!做题才能更好的理解步骤!

答:
这里插入一个例题:(我之前介绍Householder矩阵时用过)如下图:
看见这个例题你能想到什么?
题干中的
不就对应上面例题里反射前的的X向量,
不就对应着上面例题里反射后的Y向量嘛,那是不是意味着可以直接用这个公式
求解H1了?!
所以利用公式求得H1为