传感器的温度补偿-是使用传感器时常遇到的问题,尤其是需要传感器工作在一个较宽的温度范围时,这个问题更加突出。这里描述的方法是在使用某型冷媒泄漏、压力传感器时,这种方法不一定是最好的,但是它比较简单,适用范围也比较广。我在几种不同类型的传感器上应用了这个方法,效果还不错。
首先,不考虑温度的影响,在某一固定的温度下,设传感器的输入输出值可以用多项式函数表示:
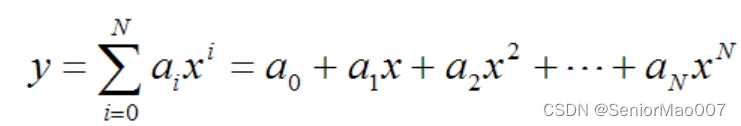
这里x 是传感器的输出(比如电压值或直接就是数字量),y 是传感器所测量的物理量的真实值。实际上,只要传感器的响应可以表示为单调连续函数,就可以利用多项式函数来逼近到任意精度,因此,一般情况下上面的式子是可以成立的。ai可以根据实验数据利用最小二乘拟合(LMS)的方法计算出来,唯一需要注意的是对于N次多项式,至少需要N+1个数据点才可以计算出。实际应用中,N的取值不宜过大,一般取为4以下就足够了,而数据点则是多多益善。
上面的式子可以写成矩阵的形式:
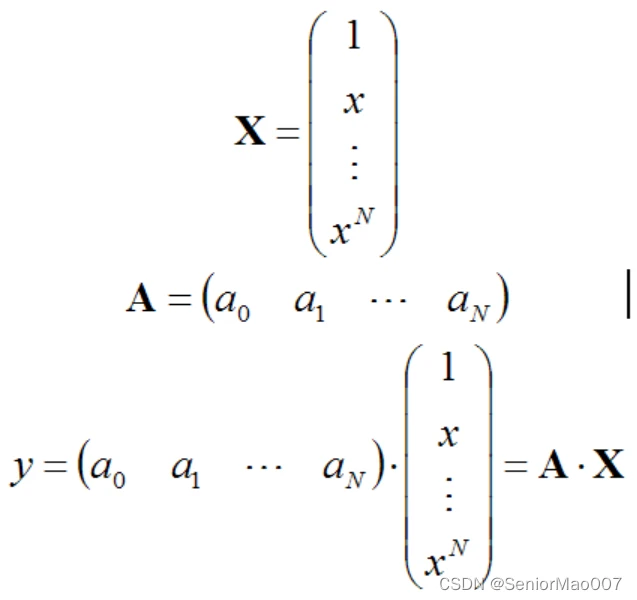
然后考虑温度的影响,不同温度下,上面公式中ai的 会发生变化。也就是说ai是温度t 的函数。类似的,也可以用多项式函数来逼近:
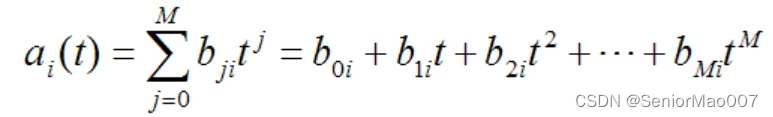
最终输出则可以表示为:
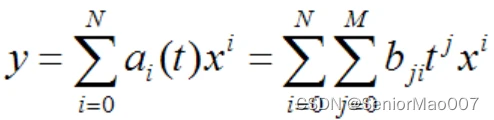
只要将这里的bij 确定下来就可以完成温度修正工作了,同样,上面的公式也可以表示为矩阵形式。
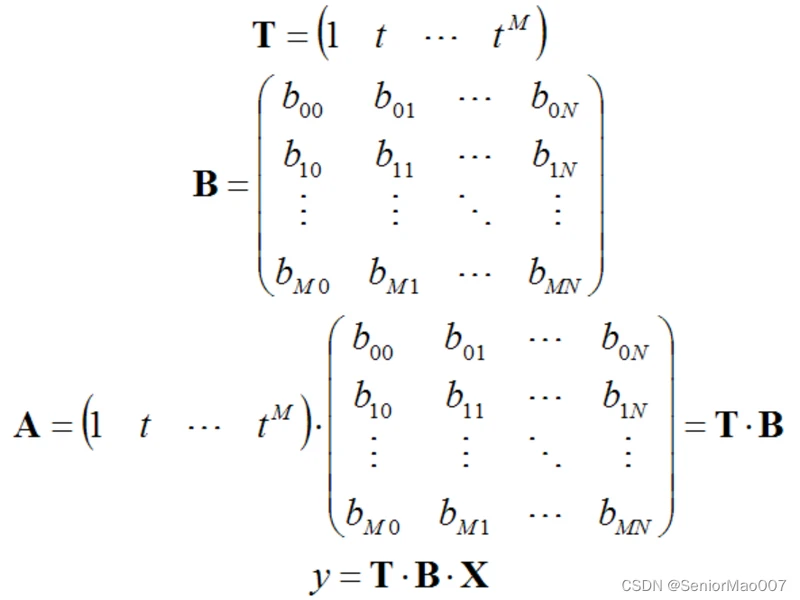
写为矩阵形式后的表达式非常的简洁,同时也易于在程序中实现。下面再多说一句,多项式函数可以通过一个小小的变型来减少乘法的次数。
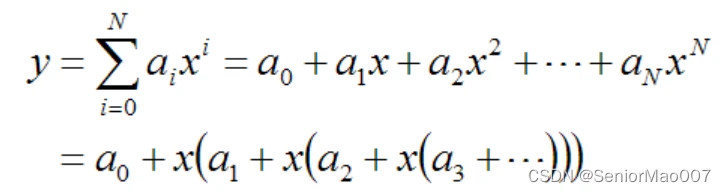
这种方法称之为多项式的Horner 算法,也被称为秦九韶算法(虽然知道这个名称的人不多)。
上面的计算都是假设bji已经求出来了,但还都没有说明如何计算bji。下面将讨论这个问题。最直观的方式就是在一系列不同温度下,用最小二乘拟合的方法计算出一系列的多项式系数ai(t)。ai(t)是M次多项式函数,因此我们至少要计算出M+1个不同温度下的系数,也就是说要至少先进行M+1次多项式拟合。然后根据ai(t)拟合出bji,很显然,这里又需要进行N+1次多项式拟合。前后两次总共要进行至少M+N+2 次的多项式拟合才能求出所有的系数。
另一种方法是直接去求所有的bji。将所有的bji排成一个列向量:
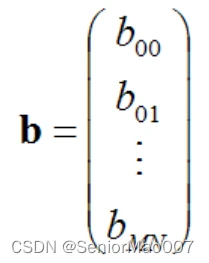
定义一个辅助矩阵:

上述公式中的下标是标注的是第几次的测量值,xp表示第p个测量值。
则传感器的经过温度修正后的测量值为:
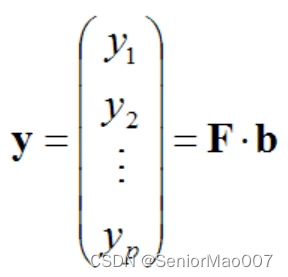
而传感器测量量的真实值为:
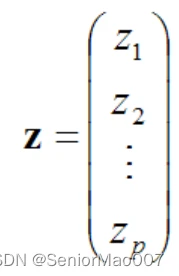
则我们的目标就是求b使得矢量 y-z 最小,这个最小如果是在2-范数的意义下的最小则是最小二乘拟合。这也就等效于求下列线性代数方程的最小二乘意义下的最优解。
![]()
这个方程的解法很多,比如说转换成下面的普通的线性代数方程:
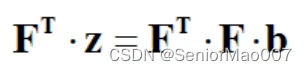
上式中FT是F的转置。其他的方法还有奇异值分解一类的数值算法。想详细研究这个问题的话可以参考各种版本的数值分析课本。
总结,本文描述的方法比较简单、粗暴,之所以这么说是因为它不去探究温度漂移的物理本质,只是用简单的多项式函数来补偿温漂的结果。但就是因为它不依赖于某个具体的物理模型,可应用的范围才会很广。
