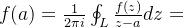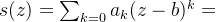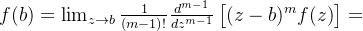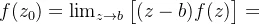- 复数的性质
- 复数
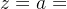 可表示为
可表示为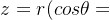
- 复数相乘时,模相乘,辐角相加。复数相除时,模相除,辐角相减
- 欧拉公式
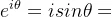 ,
,
- 复数
- 区域
- 开集
- 设G为一平面点集,z0为G中任意一点,如果存在z0的一个邻域,使该邻域的所有点都属于G,那么称z0为G的内点。如果G内每一个点都是内点,那么G称为开集。
- 区域
- 平面点集D称为一个区域,如果D是开集且D是连通的
- 边界
- D在复平面上,如果点P不属于D,但在P的任何邻域内都包含有D中的点,那么,这样的点称为D的边界点。D的边界点的全体称为D的边界,一般用L表示。
- 闭区域
- 区域D和它的边界L一起构成闭区域
- 单连通域与复连通域
- D为复平面上的一个区域,在其中作任一条简单的闭曲线,而曲线内部总属于D,则称D为单连通区域,否则为复连通区域
- 开集
- 复变函数
- 一对一或者一对多
- 单值函数
- 多值函数
- 复变函数的极限
- 就是极限。。物理系的嘛,不用这么细致。
- 几何意义
- 性质
- 可加
- 可乘
- 可除(除数不为零)
- 复变函数的连续性
- 函数在某点连续的定义
- 设w=f(z)是在区域D中定义的单值函数,并且z0为D的内点,如果任给实数
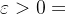 ,存在实数
,存在实数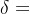 ,
,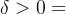 ,当D内的z满足
,当D内的z满足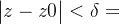 ,有
,有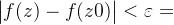 ,即
,即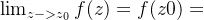 ,函数连续
,函数连续
- 设w=f(z)是在区域D中定义的单值函数,并且z0为D的内点,如果任给实数
- 连续函数
- 就是定义域上都连续呗。。。物理系的嘛,不用这么细致。
- 函数在某点连续的定义
- 导数
- 复变函数可导的必要条件
- C.R.条件
- 复变函数可导的必要条件
- 解析函数
- 若w=f(z)在z0及其邻域上处处可导,则f(z)在z0解析;若w=f(z)在B上任意点可导,则f(z)在区域B解析
- 解析函数的性质
- 调和性
- 解析函数的实部与虚部都是调和函数
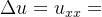
- 正交性
- 解析函数的实部与虚部梯度正交
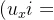
- 调和性
- 一些初等函数的定义和计算
- 指数函数
- 解析性
- 对数函数
- 幂函数
- 三角函数与双曲函数
- 反三角函数
- 指数函数
- 解析函数的性质
- 若函数f(z)=u+iv在区域B上解析,则:u(x,y)=C1 v(x,y)=C2 是B上两组正交曲线簇
- 某区域上的解析函数在该区域上有任意阶导数
- 积分
- 路积分
- 柯西定理
- 如果f(z)在单连通闭区域B上解析,L为B的边界线,a为B内的任意一点,则
- 意义
- 解析函数的可导性:一次可导,无限次可导
- 解析函数的整体性:边界值完全决定内部值
- 应用
- 模数定理:f(z)在闭区域解析,|f(z)|在边界上取最大值
- 刘维定理:全平面上有界的解析函数必为常数
- 如果f(z)在单连通闭区域B上解析,L为B的边界线,a为B内的任意一点,则
- 级数
- 幂级数展开
- 复级数
- 收敛性判别法
- 比值法
- 根值法
- 收敛性判别法
- 幂级数和泰勒展开
- 形式
- 收敛域
- 一致收敛性
- 泰勒展开
- 泰勒定理
- 一个在圆|z-b|=R内解析的函数f(z)可以展开为幂级数
- 该幂级数在圆|z-b|=R内收敛
- 以b为中心的展开式是唯一的
- 系数
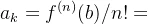
- 应用积分公式,也可为
- 泰勒定理
- 形式
- 双边幂级数和洛朗展开
- 负幂级数
- 双边幂级数=正幂级数+负幂级数
- 洛朗展开
- 一个在环R1<|z-b|<R2内解析的函数f(z)可以展开为双边幂级数
- 该幂级数在环内收敛
- 同一环域中的洛朗展开式是唯一的
- 洛朗系数
- 孤立奇点
- 奇点
- 函数的非解析点
- 孤立奇点
- 定义
- 存在解析领域的奇点
- 判断
- 只有有限个奇点的函数不存在非孤立奇点
- 定义
- 奇点
- 复级数
- 幂级数展开
- 留数定理
- 留数的定义
- 复函数f(z)在z=z0的领域围道积分的结果
- 当z0为f(z)的解析点时,结果为零
- 当z0为f(z)的孤立奇点时,结果通常为一个非零值
- 计算
- 一般情况下,孤立奇点的留数等于在该点领域洛朗展开的负一次项的系数
- 极点情况
- m阶极点的留数
- 单极点的留数
- m阶极点的留数
- 留数定理
- 定理
- 设函数f(z)在回路L所围区域B内除有限个孤立奇点外解析,在对应的闭区域上除孤立奇点外连续,则
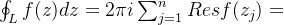
- 设函数f(z)在回路L所围区域B内除有限个孤立奇点外解析,在对应的闭区域上除孤立奇点外连续,则
- 定理
- 留数的定义
- 一对一或者一对多
- 复球面与无穷远点
- 复球面(复数球)
- 复球面与复平面相切于原点
- 无穷远点
- 模为无限大的复数
- 全平面与开平面
- 开平面为不含无穷点的复平面
- 复球面(复数球)
复数是数域吗
复数的性质 复数可表示为 复数相乘时,模相乘,辐角相加。复数相除时,模相除,辐角相减 欧拉公式, 区域 开集 设G为一平面点集,z0为G中任意一点,如果存在z0的一个邻域,使该邻域的所有点都属于G,那么称z0为G的内点。如果G内每一个点都是内点,