背景
业务上需要做一个排课系统,先调研了业内友商的排课系统,同时做了算法的对比和可行性分析。
需求
排课任务:设置任务名称、学期、排课年级集合;
节次设置:设置每周上课天数,以及每天上课节次数(上午节次数、下午节次数、晚上节次数);
课程设置:设置排课科目集合,以及各个科目的总课时、连堂课时;
教师设置:设置排课老师集合,以及各个老师所带科目、所带班级;
排课规则设置:
- 不排课规则:支持多维度不排课;
- 班级不排课:某班级不允许在选择的节次排课;
- 教师不排课:某老师不允许在设置的节次排课;
- 课程不排课:某科目不允许在设置的节次排课;
- 不连堂规则:选择两个相邻节次,不允许排连堂课;例如:选择上午第一节、第二节,则不允许排连堂课;
- 优先规则:支持多维度优先;
- 课程优先:在某节次内排课,遵循某课程优先选择原则;
- 教师优先:在某节次内排课,遵循某教师优先选择原则;
- 合班规则:设置科目、班级合班后,多个班级某科目的上课时间在同一个节次;
- 单双周规则:设置某年级的单、双周课程组合;例如:单周上道法课,双周上自然课;
- 课程互斥规则:可以给多个课程设置互斥规则,设置规则的课程不会在一天内排课;
- 预排规则:预先给部分课程和老师进行排课;
- 其它规则:
- 教案齐平规则
- 周任课规则:某科目的课程分布:周内分散,周内集中;
- 日任课规则:某科目的课程分布:日内分散,日内集中;
算法
排课算法选择:
- 贪心算法: 贪心算法可以用于一些简单的排课问题,例如按照某种优先级安排课程。但在实际应用中,可能需要结合其他算法来处理更复杂的约束条件。
- 遗传算法: 遗传算法在优化问题上表现优异,可以用于优化排课方案。通过模拟自然选择和基因变异的过程,遗传算法能够搜索到比较好的解。
- 模拟退火算法: 模拟退火算法是一种全局搜索算法,适用于在搜索空间中找到全局最优解的问题。在排课系统中,可以用于搜索满足各种约束条件的最优排课方案。
贪心算法
贪心算法是一种简单而直观的算法,但它也有一些明显的局限性:
- 局部最优不一定导致全局最优:贪心算法每步都选择当前状态下的最优解,但这种局部最优并不保证最终得到全局最优解。有些问题需要考虑长远影响,贪心算法无法预测未来的局势。
- 不适用于所有问题:贪心算法通常适用于某些特定类型的问题,但对于某些问题,贪心策略可能导致次优解或者不可行解。例如,某些涉及到约束条件的问题可能无法通过简单的贪心选择解决。
- 没有回溯:贪心算法做出选择后就无法撤销,它不具备回溯的能力。如果之前的选择导致后续无法找到解,贪心算法无法进行修正。
- 对问题的依赖性:贪心算法的效果也取决于问题的性质。在某些情况下,贪心算法可能表现良好,但在另一些情况下可能效果较差。
- 可能需要排序:对于某些问题,贪心算法可能需要对元素进行排序以选择最优解。排序本身可能引入额外的复杂度。
总体而言,贪心算法是一种简单而快速的近似算法,但在解决一些复杂问题时可能表现不佳。在设计算法时,需要仔细考虑问题的特性,选择合适的算法以获得更好的解决方案。
模拟退火算法
模拟退火算法(Simulated Annealing)是一种基于统计力学中的退火过程的全局优化算法。它被广泛应用于解决组合优化问题,包括排课、旅行商问题等。
基本思想:
- 模拟退火算法通过模拟固体退火时的温度变化过程,逐步降低系统能量(目标函数值),以接受较差的解,防止陷入局部最优解。
主要步骤:
- 初始化: 随机生成初始解,并设置初始温度和冷却率。
- 温度下降:通过降低温度来控制接受较差解的概率,模拟系统的冷却过程。
- 状态转移:在当前温度下,根据一定的概率接受新解,即使新解较差。这有助于跳出局部最优解。
- 冷却: 降低温度,逐渐减小接受较差解的概率,使算法趋于稳定。
- 重复迭代:重复执行温度下降和状态转移直至满足停止条件。
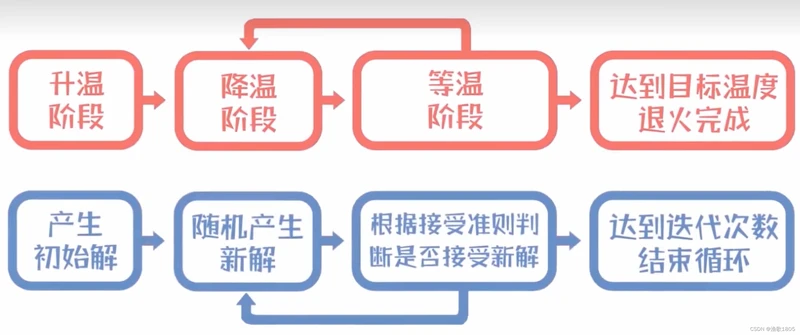
重复迭代: 重复“降温-等温”操作; 温度越高,接受非最优解的概率越大;
关键参数:
- 温度衰减函数:决定温度如何随时间变化。
- 接受概率函数: 决定在当前温度下接受较差解的概率。
优点:
- 全局搜索能力强,能够跳出局部最优解。
- 可以在一定程度上避免陷入局部最优解。
缺点:
- 参数选择较为关键,需要进行调优。
- 迭代次数较多时,算法的运行时间较长。
遗传算法
遗传算法(Genetic Algorithm)是一种模拟自然进化过程的优化算法,用于解决搜索和优化问题。它受到了达尔文的进化理论的启发,通过模拟基因的遗传、交叉和变异等操作,逐步演化出更好的解。
基本思想:
- 遗传算法模拟生物进化的过程,通过自然选择、交叉和变异等操作,从当前一组解中生成新一代的解,逐步优化。
主要步骤:
- 初始化种群: 随机生成初始解构成初始种群。
- 适应度评估:计算每个个体的适应度,即解的优劣程度。
- 选择: 根据适应度选择个体,通常适应度高的个体被选中的概率更大。
- 交叉(Crossover):随机选取一对个体,通过某种方式交换它们的基因,生成新的个体。
- 变异(Mutation):对选中的个体进行变异,即随机改变其中的一些基因。
- 形成新种群:根据选择、交叉和变异操作,形成新一代的种群。
- 重复迭代: 重复以上步骤,直到满足停止条件。
关键概念:
- 基因:解的表示,可以是一串数字、字符串等。
- 适应度: 评估解的优劣程度的指标。
- 种群:包含多个个体的集合,每个个体代表一个解。
- 交叉和变异概率:控制交叉和变异的发生概率。
优点:
- 适用于复杂问题的全局搜索。
- 可以并行处理多个解,适用于高维问题。
缺点:
- 参数选择较为关键,需要进行调优。
- 算法的收敛速度相对较慢。
采用方案
采用遗传算法。
总体而言,选择使用遗传算法还是模拟退火算法取决于具体问题的特性和需求。在排课问题中,如果问题具有较多的约束条件、复杂的优化目标、大规模的搜索空间等特点,遗传算法可能更具优势。
优化目标涉及多个约束条件:遗传算法适用于涉及多个约束条件的问题,而排课通常需要考虑教室容量、教师时间表、学生选课等多个约束条件。遗传算法的灵活性可以更好地处理这些复杂的约束。
搜索空间巨大:排课问题的搜索空间可能非常庞大,尤其是在大型学校或机构中。遗传算法能够更有效地搜索大规模的解空间,有助于找到更优的排课方案。
并行处理:遗传算法天生适合并行处理,可以同时处理多个个体,加速搜索过程。这在大规模排课问题中,特别是在考虑多个学院或校区时,可能会提高算法的效率。
组合优化问题:排课通常可以看作是一个组合优化问题,其中需要找到一组教室、时间和教师的组合,以最大程度满足多个约束条件。遗传算法在处理组合优化问题时表现较好。
不确定性和动态性: 排课问题可能面临一些不确定性和动态性,例如学生选课变化、临时调课等。遗传算法具有一定的鲁棒性,能够应对一些变化。
自然选择和适应度评估: 遗传算法的自然选择机制和适应度评估可以更好地模拟进化的过程,有助于找到更合适的排课方案。
交叉和变异操作的灵活性:遗传算法提供了交叉和变异操作,这些操作能够在基因组中引入新的组合,有助于探索更多的解空间。在排课问题中,这种灵活性可能更有利于生成更合理的排课方案。
算法模型
基因-节次槽
染色体-课表
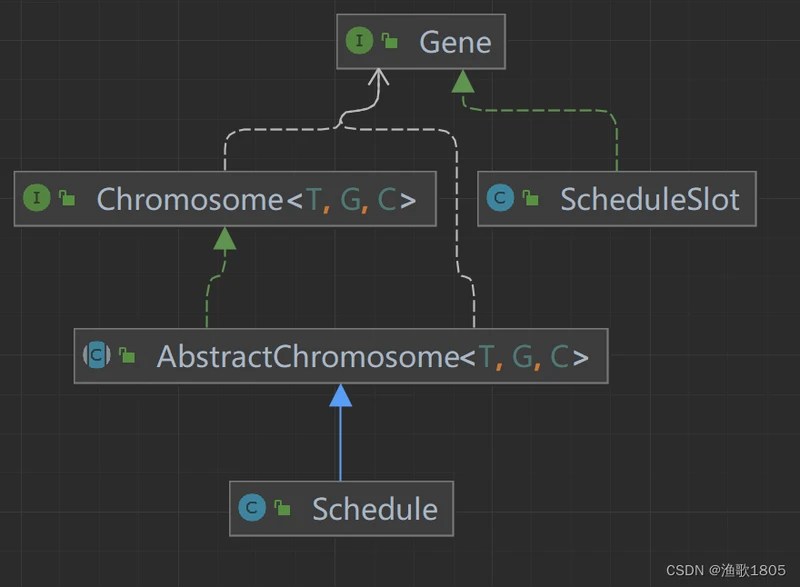
算法
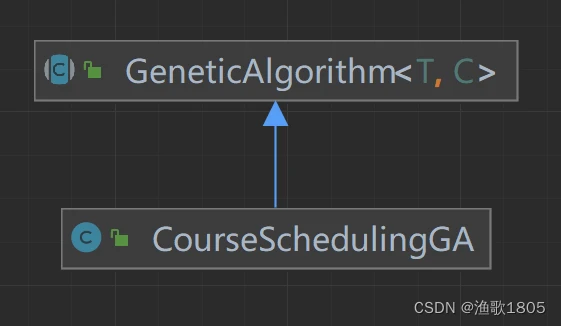
课程
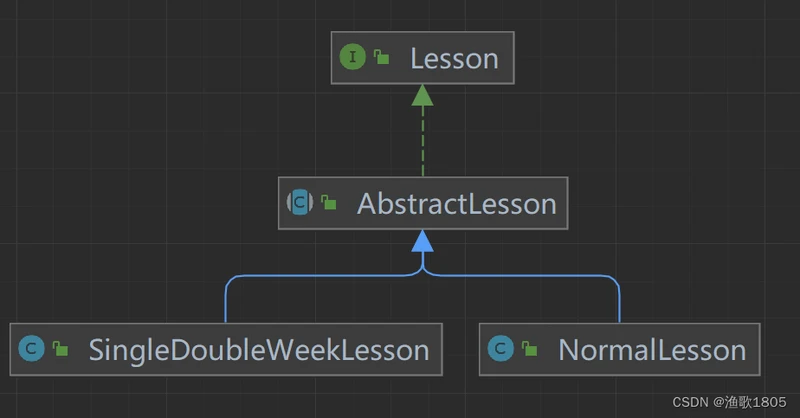
规则校验

适应度(适应度函数:影响搜索方向)

实现
遗传算法部分代码实现,实现细节因为某些原因未放出;
算法其实不复杂,复杂的是业务部分:构建课表,建立符合业务的适应度函数,各种规则的应用,以及种群演变过程中生产有效个体的逻辑;
@Slf4j
@Data
public abstract class GeneticAlgorithm<T extends Chromosome, C extends AlgorithmContext> {
/**
* 交叉概率
*/
protected float crossoverProbability = 0.8f;
/**
* 变异概率
*/
protected float mutationProbability = 0.05f;
/**
* 变异基因占比
*/
protected float mutationRatio = 0.05f;
/**
* 种群大小
*/
protected int populationSize = 50;
/**
* 迭代次数
*/
protected int iterations = 1000;
/**
* 迭代计数
*/
protected int iterationCount = 0;
/**
* 预期适应度
*/
protected double expectedFitness = 10000d;
/**
* 种群
*/
protected List<T> populations;
/**
* 上下文
*/
protected C context;
/**
* 最佳染色体
*/
protected T bestChromosome;
protected SecureRandom random = new SecureRandom();
public GeneticAlgorithm(C context) {
this.context = context;
}
/**
* 执行算法
*/
public void run() {
// 初始化种群
this.initPopulation();
while (iterationCount < iterations) {
Optional<T> bestChromosomeOptional = this.getBestChromosomeFromPopulation();
if (!bestChromosomeOptional.isPresent()) {
log.info("can't get best chromosome!");
return;
}
bestChromosome = bestChromosomeOptional.get();
log.info("iteration: {}, best fitness: {}", iterationCount, bestChromosome.getFitnessValue());
this.beforeEvolve();
if (isSatisfied()) {
return;
}
// 种群演变
this.evolvePopulation();
iterationCount++;
}
}
/**
* 是否满足
*
* @return
*/
protected boolean isSatisfied() {
if (Objects.nonNull(bestChromosome)
&& bestChromosome.getFitnessValue() >= expectedFitness) {
return true;
}
return false;
}
/**
* 种群演变前操作
* 预留,子类覆盖
*/
protected void beforeEvolve() {
}
/**
* 处理初始化失败
*
* @param invalidChromosome
*/
protected void handleInitFailure(T invalidChromosome) {
// 由具体业务实现
}
/**
* 初始化种群
*/
public void initPopulation() {
populations = new ArrayList<>(populationSize);
for (int i = 0; i < Integer.MAX_VALUE; i++) {
log.info("init population {}", i);
T chromosome = newChromosome();
// 如果达到临界值,还没初始化成功
if (i > populationSize * 5
&& populations.size() == 0) {
handleInitFailure(chromosome);
return;
}
if (!chromosome.isValid()) {
log.info("init population {}, invalid!", i);
continue;
}
populations.add(chromosome);
if (populations.size() == populationSize) {
return;
}
}
}
/**
* 获取种群中适应度最高的染色体
*
* @return
*/
public Optional<T> getBestChromosomeFromPopulation() {
if (CollectionUtils.isEmpty(populations)) {
return Optional.empty();
}
return populations.stream()
.filter(Objects::nonNull)
.reduce((c, c2) -> {
return c.getFitness().compareTo(c2.getFitness()) < 0 ? c2 : c;
});
}
/**
* 种群演变
*/
public void evolvePopulation() {
// 选择种群
// 生成子代
// 产生新种群,并替换
...
}
/**
* 种群选择
* 使用算法:轮盘赌选择
* 适应度较高的个体大概率保留,适应度较低的个体可能淘汰
*
* @return
*/
public List<T> selectPopulation() {
...
}
/**
* 选择交叉的父亲
*
* @return 返回两个染色体
*/
public ChromosomePair<T> selectCrossoverParent() {
...
}
/**
* 是否交叉
*
* @return
*/
public boolean isCrossover() {
float probability = random.nextFloat();
return probability < crossoverProbability;
}
/**
* 是否变异
*
* @return
*/
public boolean isMutation() {
float probability = random.nextFloat();
return probability < mutationProbability;
}
/**
* 创建新的染色体
*
* @return
*/
abstract T newChromosome();
/**
* 交叉
*
* @param t1
* @param t2
* @return
*/
abstract ChromosomePair<T> crossover(T t1, T t2);
/**
* 突变
*
* @param t
* @return
*/
abstract T mutation(T t);
}
