十进制、二进制、八进制和十六进制之间怎么转换?

概述

十进制：逢十进一，生活中常用的数值。
二进制：逢二进一，计算机系统使用的数制，只有0和1两个数。
八进制：逢八进一，采用0,1,2,3,4,5,6,7八个数字，在编程语言中通常用数字0开头表示八进制数。
十六进制：逢十六进一，采用0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F十六个数字，A-F分别表示十进制中的10-15，在编程语言中常用0x开头来表示十六进制数。

1.十进制和其他进制转换

1.1十进制转二进制

正数转二进制

转换规则：除二取余，倒序排序，高位补0.
在计算机中，一个字节有八位,即1 Byte = 8 bit,因此,对于16位字节的数据类型，比如short类型，最大值就是1111111111111111,转换成二进制就是65535.
如以下十进制数转换为八位二进制：

1->00000001
2->00000010
3->00000011
4->00000100
5->00000101

转换图示如下：
这里写图片描述
根据这个规则，十进制数255转换为二进制数就为11111111，如果是十六位二进制数，则在高位补0即可。

负数转二进制

转换规则：将该负数的正数进行取反，然后加1。
如：-1转换成八位二进制为11111111。
这里写图片描述

这里可能会有疑问：为什么255的二进制数和-1的二进制一样？其实是不一样的，这就要说说计算机中整数在内存中的存储方式了。

整型数据在内存中的存储方式

整型整数在内存中的存储方式和二进制有关，带符号的整数在计算机中采用二进制补码存储，不带符号的整数则采用二进制原码存储。有正负之分的整数称为带符号的整数，不分正负的整数称为无符号整数，因此，无符号整数为大于等于0的整数。
比如：int i = 1,则i变量在内存中就以无符号整数进行存储，int i = +1,则i变量在内存中就以带符号的整数的形式进行存储。

计算机在内部存储的只有0和1，如何区分符号呢？假设一个带符号的整型数据在内存中占16位，则第0位为符号位，如果为负数，则符号位为1，如果为正数，则符号位为0，比如带符号的1和-1就可以分别表示如下：
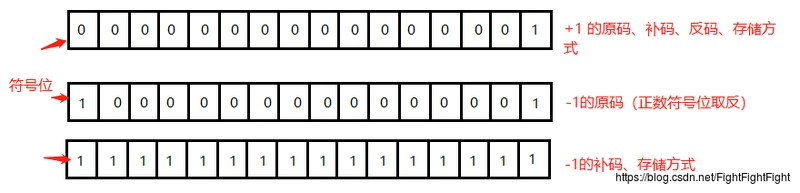
这里写图片描述

无符号整数根据二进制原码存储，因此，和带符号整数的正数存储方式相同：
这里写图片描述

但是，最大值和最小值却不同，对于带符号整数来说，第0位为符号位，因此在二进制转十进制的过程中不参与转换，其余每个位值全部为1时表示最大值，因此最大值为0111 1111 1111 1111，转换成十进制为32767。最小值为1000 0000 0000 0000(负数以补码形式存储)，转换成十进制数为-32768。因此，带符号的16位整型的取值范围为-32768~32767，如java中的short数据类型。

对于无符号整数来说，没有符号位，所以第0位也是数据一部分，因此，最大值为1111 1111 1111 1111，转换成十进制为65535，最小值为0000 0000 0000 0000，即为0，因此无符号的16位整型数据的取值范围为0~65535。

1.2.十进制转八进制

十进制转八进制和十进制转二进制很类似，如果掌握的十进制转二进制，那么自然而然就会理解十进制转八进制。

正数转八进制

转换规则：除八取余，倒序排序
如十进制12转换为八进制：
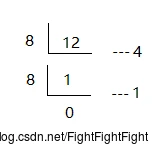
这里写图片描述
则12(10)=14(8).
在编程语言中，一般使用0开头来表示八进制，如上例中的十进制数12就可以写成014。

负数转八进制

转换规则：先将十进制负数转为二进制，再将二进制转为八进制。

1.3.十进制转十六进制

正数转十六进制

转换规则：除十六取余，倒序排序。
十六进制中用0-9,A-F来分别表示十进制中的0-15，如：

15(10) = F(16)
18(10) = 12(16)
240(10) = F0(16)

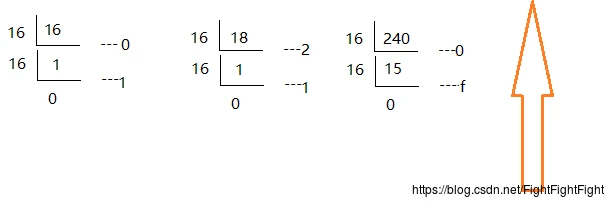
这里写图片描述

负数转十六进制

2.二进制和其他进制之间的转换

2.1.二进制转十进制

正数二进制转十进制

转换规则：首先得补齐位数，如果是正数，高位补0，负数高位补1。然后根据2的n次方转换，从右至左，n逐增最后将结果相加。如二进制数1110转成十进制为：

step1.补齐位数
假设为八位二进制数：0000 1110。
step2.按权求和：

0*2^0 = 0
1*2^1 = 2
1*2^2 = 4
1*2^3 = 8
(1110)2 = 14(10)

负数二进制转十进制

由于负数在内存中是以补码的形式存储的，因此，首先要将补码转换成原码，再进行转换。如：1111 0100转换成十进制为：

step1.补齐位数，负数高位补1，如果是16位八进制：

1111 1111 1111 0100

step2.将补码转换为原码
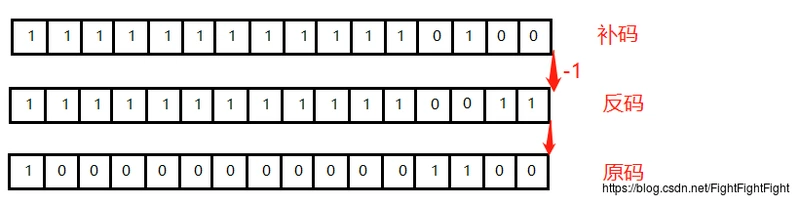
step3.按权相加,符号位不参与转换：

0*2^0 = 0
0*2^1 = 0
1*2^2 = 4
1*2^3 = 8

因此，最终结果为-12.

正数的原码、反码、补码都相同。
负数的原码：对应正数的原码符号位取反
负数的反码：符号位不变，其余各位取反
负数的补码：反码基础上加1.

2.2.二进制转八进制

由于八进制的最大数为7，转换成二进制为111，因此，二进制可以三三分组进行八进制的转换：
如：

(1001 0100)2 = (2)(2)(4) = 224(8)

对于负数二进制，转换方式相同，如：

(1111 1111 1111 1111 1111 0100)2 = (37777777764)8

2.3.二进制转十六进制

由于十六进制的最大数为F,转换成二进制为1111，因此，二进制可以四个一组进行十六进制转换：
如：

(1110)2 = E(16)
(1111 1101)2 = FD(16)

对于负数二进制，转换方式相同：

(1111 1111 1111 1111 1111 0100)2 = (fffffff4)16

3.八进制和其他进制之间的转换

3.1.八进制转二进制

由于：

(000)2 = (00)8
(001)2 = (01)8
(010)2 = (02)8
(011)2 = (03)8
(100)2 = (04)8
(101)2 = (05)8
(110)2 = (06)8
(111)2 = (07)8

所以一位八进制数对应三位二进制数，因此，在八位数转二进制时，可以将一位八位数展开为三位二进制数：

(034)8 = (011100)2 = 11100

3.2.八进制转十进制

正数转十进制

在第二节分析了十进制转八进制时除八取余，而八进制转十进制时：从右至左，各项乘以8的n次方，n由0逐增，如：

(045)8 = 5*8^0+4*8^1 = (72)10
(0123)8 = 3*8^0 + 2*8^1 + 1*8^2 = (35)10

负数转十进制

对于负数转十进制，不能直接像正数转十进制一样，应首先将负数八进制转换为二进制，再通过二进制转换为十进制。
如32位的二进制数1111 1111 1111 1111 1111 1111 1111 0100表示十进制数-12、八进制数37777777764，由八进制转为十进制时，不能直接按权相加，应该首先转换成二进制，再由二进制转换为十进制：

step1.先将八进制转二进制：

1111 1111 1111 1111 1111 1111 1111 0100

step2.将二进制转十进制，由于是负数，所以先根据补码求其反码：

1111 1111 1111 1111 1111 1111 1111 0100
                                     -1
----------------------------------------
1111 1111 1111 1111 1111 1111 1111 0011

step3. 再求其原码,符号位不变，其余各位求反：

1111 1111 1111 1111 1111 1111 1111 0011
取反得：
----------------------------------------
1000 0000 0000 0000 0000 0000 0000 1100

step4. 根据原码求十进制：

1*2^2 + 1*2^2 = 12

故而转换完成。

3.3.八进制转十六进制

转换规则：先将八进制转为二进制，再将二进制四位一组转换为十六进制。正负数同适用。
如(0476)8转换为16进制的步骤如下：

step1.先将八进制转为二进制：

(0476)8 = (100111110)2

step2.将二进制转为十六进制：

(1 0011 1110)2 = (0x13E)16

4.十六进制和其他进制之间的转换

4.1十六进制转二进制

二进制转十六进制是以四位为一组，因此十六进制转二进制时，将十六进制的一位展开为4位，如：

(0x13F)16 = (0001 0011 1111)2

4.2.十六进制转八进制

十六进制转八进制时，首先将十六进制转为二进制，然后3位一组转为八进制：

(0x13F)16 = (0001 0011 1111)2 = (477)8

4.3.十六进制转十进制

正数十六进制转十进制

正数十进制转十六进制时，采用了除十六取余的方式，因此十六进制转十进制时，通过按权相加的方式，如：

(0x13F)16 = F*16^0 + 3*16^1 + 1*16^2 = (319)10

负数十六进制转十进制

负数十六进制转二进制时，应该首先将负数转换为对应的二进制，再通过二进制转为十进制，如fffffff4表示一个32位的负数，则转换时：

step1.先将十六进制转换为二进制：

(fffffff4)16 = (1111 1111 1111 1111 1111 1111 1111 0100)2

step2.现在得到负数的补码，将补码-1转成反码：

1111 1111 1111 1111 1111 1111 1111 0100
-1得:
----------------------------------------
1111 1111 1111 1111 1111 1111 1111 0011

step3.得到反码后，符号位不变，其余各位取反得到原码：

1000 0000 0000 0000 0000 0000 0000 1100

step4.将二进制原码转为十进制：

1*2^2+1*2^3 = 12

最后加上符号得到最终的结果为-12.

5.总结

1.十进制转八进制/十六进制时，正数可以除8/16取余，倒序排序的方式转换，也可以先转换为二进制，再转为八/十六进制；负数则只能先转换为二进制，再由二进制转换为十进制。
2.八进制/十六进制转换成十进制时，正数可以按权相加转换，也可以先转换为二进制，再转为十进制；负数则只能先转换为二进制，再由二进制转换为十进制。
3.二进制是八进制、十进制、十六进制之间转换的一个桥梁。