1、背景：冷战期间，美苏声称为了保卫自身的安全，实行“核威慑战略”，核军备竞赛不断升级。
随着苏联的解体和冷战的结束，美苏双方通过一系列核裁军协议。
核威慑战略：认为对方可能发起第一次核打击，即倾其全部战略核导弹攻击己方的核导弹基地。
己方在经受第一次核打击之后，应该保持足够的核导弹，给对方重要目标以毁灭性的打击。
2、问题：在什么情况下双方饿核军备竞赛不会无限扩张，而存在暂时平衡状态？
估计平衡状态下双方拥有的最少核武器数量，这个数量受哪些因素影响？
当一方采取加强防御，提高武器精度，发展多弹头导弹等措施时，平衡状态会发生什么变化？
3、模型假设
（1）假定双方（甲、乙）均采取核威慑战略。
（2）以双方（战略）核导弹数量描述核军备的大小。
（3）在任何一方实施第一次核打击时，假定一枚核导弹只能攻击对方的一个核导弹基地，每个基地只存放一枚导弹。
（4）不同的导弹尽可能攻击对方的不同的核基地。
（5）摧毁这个基地的可能性是常数，它由一方的攻击精度和另一方的防御能力决定。
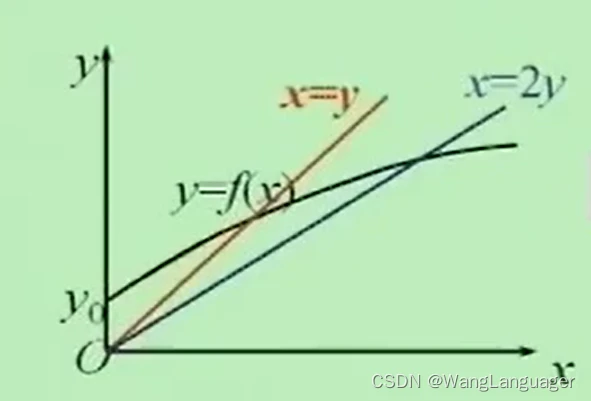
4、图的模型
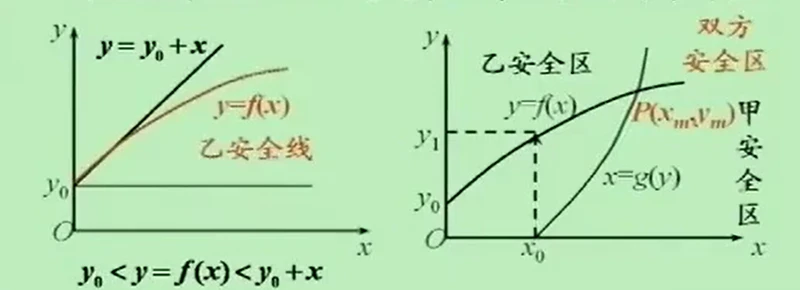
（1）
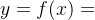，甲有x枚导弹，乙所需的最少导弹数（乙安全线）
（2）
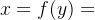，乙有y枚导弹，甲所需的最少导弹数（甲安全线）
（3）当x=0时，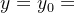
，
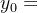表示乙方的威慑值
当y=0时，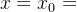
，
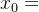表示甲方的威慑值
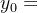表示甲方实行第一次打击后已经没有导弹，乙方为摧毁甲方工业、交通中心等目标所需的导弹数量。
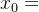表示甲方实行第一次打击后已经没有导弹，乙方为摧毁甲方工业、交通中心等目标所需的导弹数量。
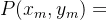——最佳平衡点，甲、乙双方拥有最少核武器达到平衡
5、分析模型
（1）乙方残存率S：甲方一枚导弹攻击乙方一个基地，基地未被摧毁的概率。
（2）当x<y时，甲方以x枚导弹攻击乙方y个基地中的x个，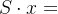
个基地未被摧毁，
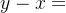个基地未被攻击。
剩余基地数量：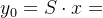
(3)当x=y时，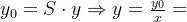
(4)当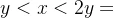
时，
乙的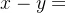
个基地被攻击2次，
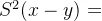个未被摧毁。
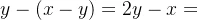个被攻击1次，
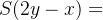个未被摧毁。
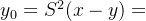
(5)当x=ay时，
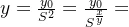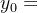，表示威慑值，S表示残存率
利用微积分知识可知y是一条上凸的曲线，而且：
①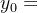变大，曲线上移，变陡
②S变大，y减小，曲线变平
6、模型解释
（1）甲方增加经费保护及疏散工业、交通中心等目标
会导致：①乙方威慑值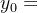变大，（其他因素不变的情况下）
②乙方安全线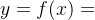上移
③平衡点P变更为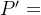
,也会上移和右移
④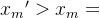
，
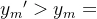
⑤最终会导致甲方的被动防御也会使双方军备竞赛升级。
（2）甲方将固定核导弹基地改进为可移动发射架
①乙方安全线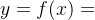不变，甲方残存率变大，威慑值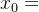不变。
②x减小，甲方安全线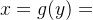
向y轴靠近。
③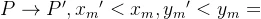
④甲方这种单独行为，会导致双方的核弹头数量减少。
（3）双方同时发展多弹头导弹，每个弹头可以独立地摧毁目标。
（x,y）仍为双方核导弹的数量。
①双方威慑值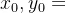
和残存率S都减小
②对于乙方安全线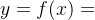
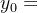减小，导致y下移，曲线变平。
S减小，导致y增加，曲线变陡。
双方导弹最终增加还是减小，需要更多的信息来进行更详细的分析。
7、核军备竞赛建模过程评述
（1）对“核威慑战略”做了一些合理、简化假设，用图的模型描述双方核武器相互制约，达到平衡的过程。
（2）提出安全曲线的概念，给出它的一般形式。
（3）通过更精细饿分析找到影响安全线的参数：威慑值和残存率。
给出安全线的分析表达式。
（4）利用模型对核军备竞赛中的一些现象作出合理解释。
（5）由于信息的非对称性，双方对平衡点达成共识比较困难。
