1. 定义与性质
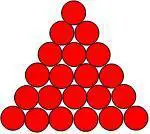
- 能堆成三角形的数总和
1 + 2 + ⋯ + n = n ( n + 1 ) 2 1+2+\cdots+n=\frac{n\left(n+1\right)}2 1+2+⋯+n=2n(n+1)
- 第 1 行 1 个数为(1),第 2 行 2个数为 (1,2),…,第 n 行 n 个数为 (1, 2, 3, …, n):
1 + ( 1 + 2 ) + ( 1 + 2 + 3 ) + ⋯ + ( 1 + 2 ⋯ + n ) = n ( n + 1 ) ( n + 2 ) 6 1+(1+2)+(1+2+3)+\cdots+(1+2\cdots+n)=\frac{n(n+1)(n+2)}6 1+(1+2)+(1+2+3)+⋯+(1+2⋯+n)=6n(n+1)(n+2)
2. 杨辉三角
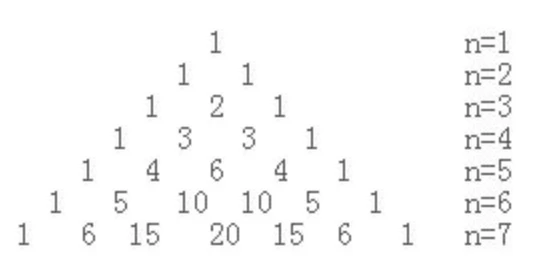
- 二项分布的角度:
- 各行分布:
- 第1行为 C(0, 0)
- 第2行为 C(1, 0), C(1, 1)
- 第3行分别为 C(2, 0), C(2, 1), C(2, 2)
- 第4行分别为 C(3, 0), C(3, 1), C(3, 2), C(3, 3)
- 由二项分布: ( n 0 ) + ( n 1 ) + ⋯ + ( n n − 1 ) + ( n n ) = ( 1 + 1 ) n = 2 n \binom n 0+\binom n1+\cdots +\binom n {n-1}+\binom nn=(1+1)^n=2^n (0n)+(1n)+⋯+(n−1n)+(nn)=(1+1)n=2n可知:
- 第一行各个数的和:1
- 第二行各个数的和:2
- 第三行各个数的和:4
- …
- 各行分布:
- 每一行从左到右拼成一个独立的数,分别为 1, 121, 1331, 14641, …,
- 1 1 n − 1 11^{n-1} 11n−1
