我的新博客：http://ryuzhihao.cc/

本文在我的新博客中的链接：http://ryuzhihao.cc/?p=601

前些天研究了一下棋谱2333，然后就顺便写了这个程序。整个程序是基于Qt开发，就UI而言毫无亮点，所以接下来的文章将主要介绍五子棋电脑AI的设计。可能这会是一篇非常长的博文。

在正文开始之前，首先贴一下程序的下载链接以及程序截图~

一、程序预览

1 下载地址：

https://pan.baidu.com/s/1nuJiPDJ

2 程序截图：

图1 五子棋程序截图

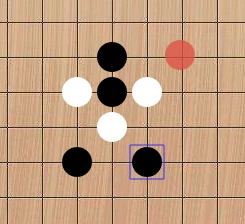
图2 一次着棋回合 （红色为鼠标位置，紫色框为电脑上次着棋位置）

二、五子棋基本棋型

在设计AI之前，我们应该先告诉电脑何种棋型容易获胜，什么情形下应该进攻，什么情形下应该采取防守策略。所以为了设计更好的AI，需要先对五子棋棋型有些了解，在紧接着的章节里，我在介绍棋型的同时，也会顺便介绍一些算法的实现策略。

       【约定】 _为空，○为敌方棋子，●为己方棋子

① 连五：五颗棋子连在一起，获得胜利。

●●●●●

② 活四：四颗棋子相连，同时两端均为空（即有两个位置可以形成连五）。

当活四出现的时候，对方如果单纯采取防守策略时，已经无法阻挡自己的胜利（除非对方采取进攻策略，一招制胜，我们的程序也要注意这一点）

_●●●●_

③ 死四：四颗棋子，但只有一个位置可以形成连五。

相比活四而言，死四的威胁要小的多，因为这个时候对方只要跟着防守即可。但是死四出现时，其优先级应当比下面提到的活三要高（因为活四虽能轻易破解，但是对于双方都意味着一步结束比赛，故必须注意）。

_●●●●○

●_●●●

 ●●_●●

④ 活三：可以形成活四的三，有如下常见的几种棋型：

活三棋型是进攻时最常见的棋型。因为活三之后，如果对方不予理会，则可直接一手变成活四。因此当敌方活三出现时，需要进行防守。

 _●●●_

_●_●●_

⑤ 死三：能够形成死四的三。死三与活三相比，危险系数降低了不少，因为死三即便不去防守，下一手也只能形成死四，我们仍然可以防守的住。

⑥ 活二：能够形成活三的二。活二看似人畜无害，因为它只下一手便能形成活三，等形成活三我们仍能防守。但其实活二其实很重要，因为在开局阶段，如果能够形成较多的活二棋型，那么当我们将活二变成活三时，就能将自己的活三绵延不绝，让对手防不胜防。

_ _●●_ _

_●_● _

_●_ _●_

⑦ 死二：能够形成眠三的二。

三、着棋估值

着棋估值，是整个程序中最关键的一步。因为估值方法，是教会电脑判断如何根据当前棋盘形式，找到最适合的着棋位置的关键。而一个好的估值方法，也能大大提高电脑AI的获胜概率。

事实上，如果不需要让电脑AI具有预见未来若干步的本领，那么只要实现这一步即可。并且，如果仅仅有着棋估值作为AI判断的考量标准时，电脑AI也能有不错的表现（如果不小心，你会很容易输给它）。

着棋估值，我们用这样的函数原型描述它：

int envaluate ( Point p , Type who);

     其中，参数p表示当前估值的棋盘坐标点，who表示站在哪一方的角度进行估值（是玩家？还是电脑？）。

那么，当我们不需要电脑有远见的能力时，我们可以用如下代码从整张当前棋盘中，找到最合适的落脚点：

/// 轮到AI的回合
void isTimeToAI()
{
  Point bestPos1;  // 最佳的进攻位置
  Point bestPos2;  // 最佳的防守位置

  // 首先，分析采取进攻策略时的情况
  // 当前棋盘中采取进攻策略的最高权重max1
  int max1 = 0;


  for(int r=0; r<size; r++) // 双层循环遍历棋盘
  {
    for(int c=0; c<size ;c++)
    {
      Point cur(r,c);  // 当前查询的位置

      if(isNull(cur))  // 如果已经有棋子了
        continue;
      
      int value = envaluate(cur,COMPUTER);

      if(max1 > value)
      {
        max1 = value;
        bestPos1 = cur;
      }
    }
  }

  // 然后，分析采取防守策略时的情况
  // 当前棋盘中采取防守策略的最高权重max2
  int max2 = 0;


  for(int r=0; r<size; r++) // 双层循环遍历棋盘
  {
    for(int c=0; c<size ;c++)
    {
      Point cur(r,c);  // 当前查询的位置

      if(isNull(cur))  // 如果已经有棋子了
        continue;

      int value = envaluate(cur,PLAYER);

      if(max2 > value)
      {
        max2 = value;
        bestPos2 = cur;
      }
    }
  }

  // 从防守和进攻中找到最好的情况。
  if(max1 >= max2)  // 进攻
  {
    dropChessAt(bestPos1);
  }
  else             // 防守
  {
    dropChessAt(bestPos2);
  }
}

上述代码，先从进攻的角度去寻找，又从防守的角度去寻找。如果进攻的优先级更高，那么采取进攻策略；反之，采取防守策略。

那么，判断每个着棋位置的棋型envaluate(p, cur) 函数应该如何去定义？

根据第二章节的分析，我们可以设定如下棋型的权值顺序：

连五 > 活四 > 死四 > 活三 > 活二 （略大于）死三 > 死二 > 其他棋型 

       那么，我们在给定上述权值顺序时，便可以得出如下的估值函数代码：

int BoardAI::envaluateAt(Point p,int who)   // 是哪一个玩家下在p位置
{
    int value = 0;
    int opposite = (who == PLAYER)?COMPUT:PLAYER; // 敌对方是谁

    for(int i=0; i<8; i++)  // 8个方向
    {
        //判断是否存在 *11110 ("活四" 必胜 没办法去赌了)
        if(getPointAt(p,i,1) == who && getPointAt(p,i,2) == who
                && getPointAt(p,i,3) == who && getPointAt(p,i,4) == who
                && getPointAt(p,i,5) == EMPTY)
        {
            value+=400000;  // 40万
        }

        // 判断是否存在 21111* （死四A）  如果是己方则下子获得胜利，对手的话要竭力去赌
        if(getPointAt(p,i,1) == who &&getPointAt(p,i,2) == who
                && getPointAt(p,i,3) == who &&getPointAt(p,i,4) == who
                && getPointAt(p,i,5) == opposite)
        {
            value += 300000; // 30万
        }

        // 判断是否存在 111*1 （死四B）
        if(getPointAt(p,i,-1) == who &&getPointAt(p,i,1) == who
                && getPointAt(p,i,2) == who &&getPointAt(p,i,3) == who)
        {
            value += 300000; // 30万

        }

        // 自行添加其他棋型的判断，这里省略掉了，同上。

        // 判断是否存在 1*001（死二）
        if(getPointAt(p,i,-1) == who && getPointAt(p,i,1) == EMPTY
                && getPointAt(p,i,2) == EMPTY && getPointAt(p,i,3) == EMPTY)
        {
            value +=100;
        }
         
        // 周围如果已有棋子数目比较多的话，适当增加一下权值

        value += (getPointAt(p,i,-1)== who
                  +getPointAt(p,i,-1)==opposite)*25;
    }
    return value;
}

在上面的代码中，出现了一个函数：

int getPointAt (Point p, int dir, int offset);

      其中，p为当前探测的中心点，dir为探测方向，Offset是距离p的偏移量，返回值为该点的棋子类型（空、白棋、黑棋）。通过这个函数，我们可以借助查询距离p任意方向，且任意长度的点的类型。其具体的实现如下：

QPoint m_offset[8] = {
    QPoint(0,-1),QPoint(1,-1),QPoint(1,0),QPoint(1,1),
    QPoint(0,1),QPoint(-1,1),QPoint(-1,0),QPoint(-1,-1)
};

int BoardAI::getPointAt(Point p, int dir, int offset)
{
    int r = p.row;
    int c = p.col;

    r = r + offset*m_offset[dir].y();
    c = c + offset*m_offset[dir].x();

    if(r<0 || c<0 || r>=BOARDSIZE || c>=BOARDSIZE)
        return OUTRANGE;

    return board[r][c];
}

四、有远见的电脑AI？

通过前面的分析，我们已经能够得到一个还不错的AI了，或许我们也可以称之为一个不错的棋手。但是现实中遇到的高手，大多能够预见未来的若干步，并分析出当前最佳的策略。一则，可以避免未来可能发生的槽糕的情形；二则，可以为未来可以构建的奇招打下基础。

那么，应该如何实现这样有远见的AI呢？

这里，我们采用构建博弈树的方式，选择能够导致未来最佳情形的策略。所谓博弈树的构建，其实是以当前棋局为根节点，然后下一步，我们可能在当前的任意一个空位着棋，那么生成相应数目的叶节点（即每个叶节点，是我们在其父结点的基础上，着下一棋的结果）。

那么这样，我们重复多次之后，就有可能生成如下的博弈树：

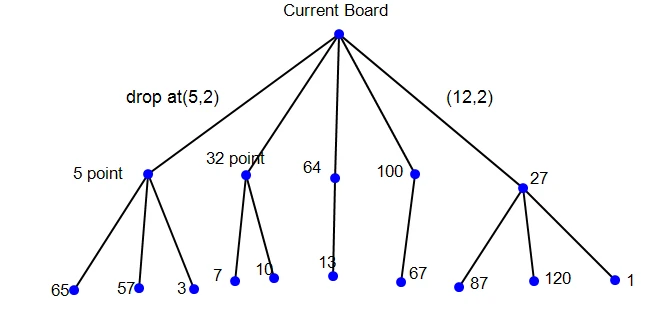
这里，我们只需要简单的递归即可实现这个步骤。我们只需分析每个叶节点的权值（也就是未来几步的情形），从中选取最好的情形，并按照这个策略着棋即可。

当然，我们可能会遇到一些可能的情况。比如中间某步时，敌方/己方获得胜利，那么我们可以赋这种情形一个较大的权重，但是仍要继续遍历，因为有可能剩余的步骤里，敌方/己方可能在较短的路径长度（PL）结束游戏。