分层建图
首先来一道题,题意是这样的:
给定一张有向图(游戏地图),一对起点和终点,每个点代表一个城市,你从起点开车到终点,每次在两个城市间移动需要1h。每个点(城市)都有五种可能的情况:
1.该点没有任何道具;
2.该点有阻碍物需要停止1h;
3.到达该点时游戏失败(保证起点和终点不为3);
4.该点有氮气,接下来连续两次移动速度加倍(倍数不可叠加,次数可以);
5.该点有沙子,接下来连续两次移动速度减半(同上);
求从起点到终点最快用时,如果不能到达终点输出-1.
分析题目,单源最短路径,很显然就该用 SPFA dijkstra算法。对于各类点,遇到1不管,2的话将该点的出边权值(用时)加一,3的话删除连接这个点的所有边。
但是,4和5两种情况怎么处理?怎么实现同一条边权值(用时)加倍和减半的操作,怎么让1、0.5、2三种边权同时存在于一条边上呢?
换个想法,与其纠结在一条边上进行的多次修改,不如把所有可能的权值都建立一条边,也就是说,分层建图。
(当然,这并不是什么算法,只是一种建图的技巧/思想。
就这题而言,可以将图分为三层,分别叫做G1G2G3,G1的边权都为1,G2都为0.5,G3都为2,初始在G1层的起点。对于每一个第四类点(氮气),我们可以向G3的同一点连一条无权边(权值为0),然后对于所有和该点距离在2以内的G3层点向G1连一条无权边,如图所示其中G1.1为氮气:
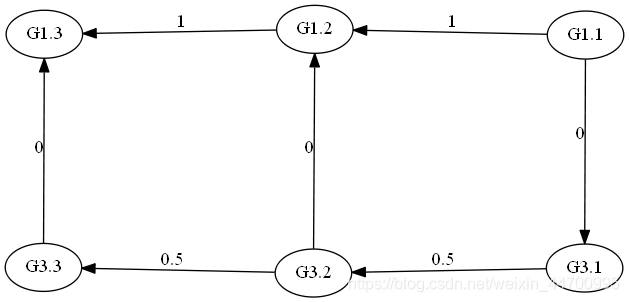
(今天刚学Graphiviz,画的太丑,暂时凑合着看吧)
同理,遇到第五类点作相同处理,这题就变成裸的dijkstra啦。
下面来做道题目体会一下:
bzoj2763: [JLOI2011]飞行路线
给出 n n n个点, m m m条边的无向图,一对起点和终点,给你 k ( k ≤ 10 ) k\ (k\le10) k (k≤10)次将当前边权变为 0 0 0
