数字信号处理翻转课堂笔记11
The Flipped Classroom11 of DSP
对应教材:《数字信号处理(第五版)》西安电子科技大学出版社,丁玉美、高西全著
一、要点
1、数字滤波器的分类、技术指标和设计方法;
2、模拟滤波器的设计指标参数;
3、5种模拟滤波器的特点比较;
4、巴特沃斯和切比雪夫模拟低通滤波器的设计原理(难点,一般了解);
5、巴特沃斯、切比雪夫模拟低通滤波器的设计方法和步骤(重点);
6、利用MATLAB设计巴特沃斯、切比雪夫、椭圆滤波器的函数和步骤。
二、问题与解答
1、理想数字选频滤波器的频率响应和理想模拟选频滤波器的频率响应有何区别?为什么会有这种区别?什么是IIR数字滤波器?什么是FIR数字滤波器?IIR滤波器和FIR滤波器的系统函数有什么不同?数字滤波器的直接设计法和间接设计法分别指的是什么?
2、模拟/数字选频滤波器的幅频特性技术指标主要包含哪几个参数?数字滤波器截止频率的取值范围是什么?结合滤波器的应用,解释每个参数的含义和作用(会对滤波结果产生何种影响)。
3、

4、自行拟定模拟低通滤波器技术指标,按照滤波器设计步骤(不采用MATLAB设计函数),分别设计出模拟巴特沃斯和切比雪夫I型滤波器(两种滤波器的技术指标相同),画出所设计滤波器的幅频响应曲线和零极点图。①对设计结果进行比较分析,讨论这两种滤波器阶次和幅频特性曲线方面的差异,并据此总结两种模拟滤波器的设计方法和步骤。②比较这两种滤波器的零极点分布特性,结合零极点图和幅频响应曲线,讨论幅频响应曲线形状与零极点分布的关系(回顾信号与线性系统相关内容)。
5、以上题同样的技术指标,利用MATLAB设计函数,分别设计出模拟巴特沃斯、切比雪夫(任选I型或II型)、椭圆滤波器,画出所设计滤波器的幅频特性曲线(如果上一题设计未能正确完成,可以在这里一并画出零极点图并完成第(4)题的相关分析),对比分析各滤波器在阶次和幅频特性曲线方面的差异,并与上一题的对应结果进行比较。
6、设定相同的低通滤波器阶次、通带截止频率、通带和阻带衰减,利用MATLAB设计函数分别设计出相应的模拟巴特沃斯、切比雪夫(任选I型或II型)、椭圆滤波器(通过尝试不同的阻带截止频率,使得各类滤波器的阶次相同),画出所设计滤波器的幅频特性曲线,比较不同类型滤波器阻带截止频率和过渡带宽度的差异。
7、设定相同的低通滤波器阶次、通带衰减、通带和阻带截止频率,利用MATLAB设计函数分别设计出相应的模拟巴特沃斯、切比雪夫(任选I型或II型)、椭圆滤波器(通过尝试不同的阻带衰减数值,使得各类滤波器的阶次相同),画出所设计滤波器的幅频特性曲线,比较不同类型滤波器阻带衰减的差异。
8、总结4-7题的设计分析结果,讨论不同类型低通选频滤波器的特点。在滤波器技术指标相同的情况下,哪种类型模拟滤波器的阶次最低?
1、滤波器基本概念
理想数字选频滤波器的频率响应和理想模拟选频滤波器的频率响应有何区别?为什么会有这种区别?什么是IIR数字滤波器?什么是FIR数字滤波器?IIR滤波器和FIR滤波器的系统函数有什么不同?数字滤波器的直接设计法和间接设计法分别指的是什么?
理想数字选频滤波器的单位脉冲响应是非因果且无限长的;频率响应函数都是以2π为周期的。理想模拟选频滤波器是一个因果稳定系统,单位冲激响应为实函数。
因为非因果是物理不可实现的。

2、滤波器技术指标
模拟/数字选频滤波器的幅频特性技术指标主要包含哪几个参数?数字滤波器截止频率的取值范围是什么?结合滤波器的应用,解释每个参数的含义和作用(会对滤波结果产生何种影响)。

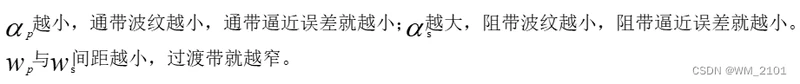
3、阶次与幅频响应形状的关系


原因:
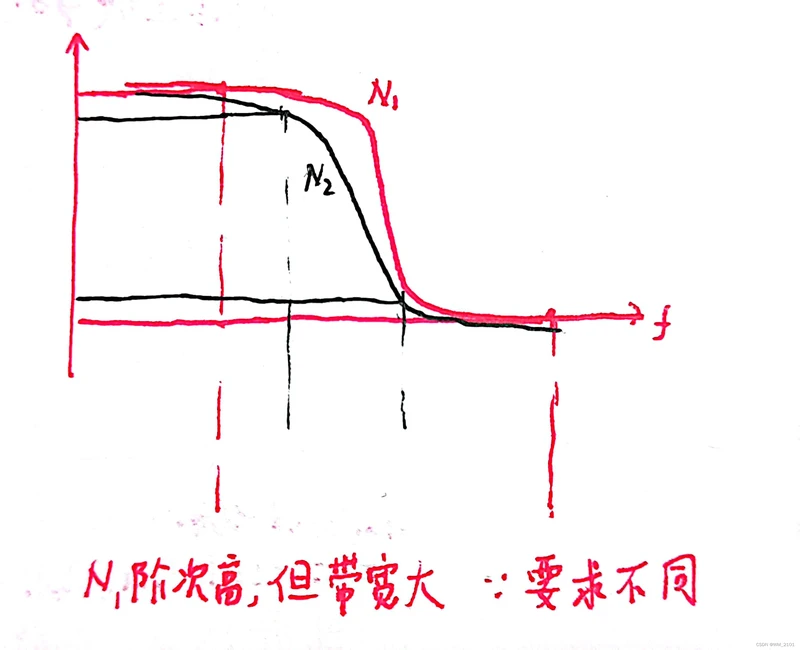
4、用matlab设计模拟滤波器并画出对应幅频响应曲线和零极点图
自行拟定模拟低通滤波器技术指标,按照滤波器设计步骤(不采用MATLAB设计函数),分别设计出模拟巴特沃斯和切比雪夫I型滤波器(两种滤波器的技术指标相同),画出所设计滤波器的幅频响应曲线和零极点图。①对设计结果进行比较分析,讨论这两种滤波器阶次和幅频特性曲线方面的差异,并据此总结两种模拟滤波器的设计方法和步骤。②比较这两种滤波器的零极点分布特性,结合零极点图和幅频响应曲线,讨论幅频响应曲线形状与零极点分布的关系(回顾信号与线性系统相关内容)。
暂未完成,后续更新


5、用matlab设计三种模拟滤波器
以上题同样的技术指标,利用MATLAB设计函数,分别设计出模拟巴特沃斯、切比雪夫(任选I型或II型)、椭圆滤波器,画出所设计滤波器的幅频特性曲线(如果上一题设计未能正确完成,可以在这里一并画出零极点图并完成第(4)题的相关分析),对比分析各滤波器在阶次和幅频特性曲线方面的差异,并与上一题的对应结果进行比较。
代码:
%% 代码:
%% 巴特沃斯滤波器
figure(1)
wp=2*pi*5000; %技术指标
ws=2*pi*10000;
Rp=2;
As=20;
[N,wpo]=buttord(wp,ws,Rp,As,'s'); %巴特沃斯滤波器
[B,A]=butter(N,wpo,'s');
k=0:511;
fk=0:20000/512:20000;
wk=2*pi*fk;
Hk=freqs(B,A,wk);
plot (fk/1000,abs (Hk));
xlabel('频率(kHz)');
ylabel('幅度(dB)');
title('巴特沃斯滤波器幅频响应');
%% 椭圆滤波器
figure(2)
wp=2*pi*5000; %技术指标
ws=2*pi*10000;
Rp=2;
As=20;
[N,wpo]=ellipord(wp,ws,Rp,As,'s'); %椭圆滤波器
[B,A]=ellip(N,Rp,As,wpo,'s');
k=0:511;
fk=0:20000/512:20000;
wk=2*pi*fk;
Hk=freqs(B,A,wk);
plot(fk/1000,abs(Hk));
xlabel('频率(kHZ)');
ylabel('幅度(dB)');
title('椭圆滤波器幅频响应');
%% 切比雪夫I型滤波器
figure(3)
wp=2*pi*5000; %技术指标
ws=2*pi*10000;
Rp=2;
As=20;
[N,wpo]=cheb1ord(wp,ws,Rp,As,'s'); %切比雪夫I型滤波器
[B,A]=cheby1(N,Rp,wpo,'s');
k=0:511;
fk=0:20000/512:20000;
wk=2*pi*fk;
Hk=freqs(B,A,wk);
plot(fk/1000,abs(Hk));
xlabel('频率(kHz)');
ylabel('幅度(dB)');
title('切比雪夫I型滤波器幅频响应');
运行结果:
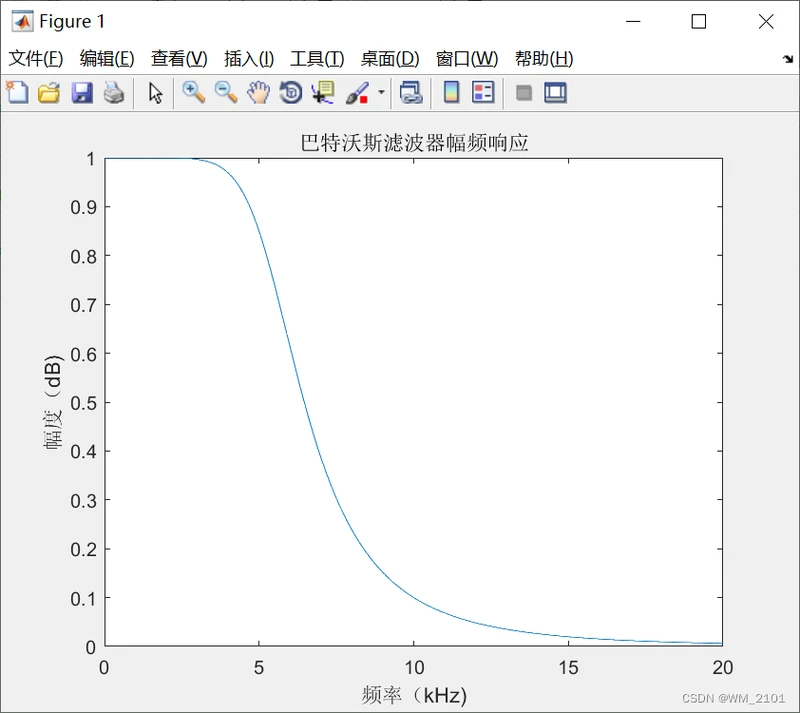
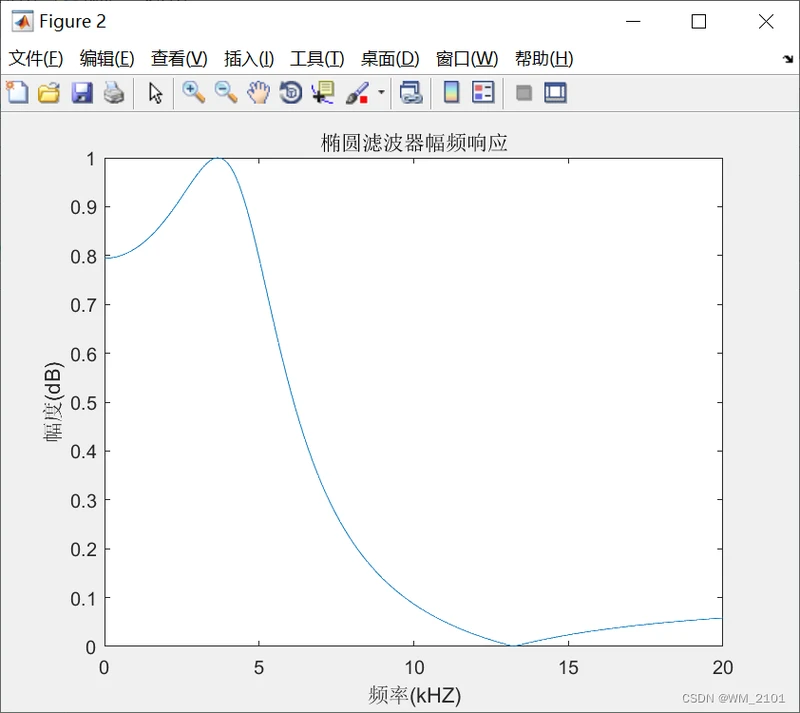
分析:
各滤波器在阶次和幅频特性曲线方面的差异:
由图可知,在相同的设计指标下,
椭圆滤波器的阶次最小,其次是切比雪夫滤波器,最后是巴特沃斯滤波器。
巴特沃斯滤波器的幅频特性曲线在通带和阻带中都是单调减函数;
切比雪夫Ⅰ型滤波器的幅频特性曲线在通带内是等波纹的,阻带内是单调下降的;
椭圆滤波器的幅频特性曲线在通带和阻带内都是等波纹的。




注意,以上只是得出了相应的滤波器参数,并不能画出图来
6、不同类型的模拟滤波器的比较(过渡带)
设定相同的低通滤波器阶次、通带截止频率、通带和阻带衰减,利用MATLAB设计函数分别设计出相应的模拟巴特沃斯、切比雪夫(任选I型或II型)、椭圆滤波器(通过尝试不同的阻带截止频率,使得各类滤波器的阶次相同),画出所设计滤波器的幅频特性曲线,比较不同类型滤波器阻带截止频率和过渡带宽度的差异。
代码:
%% 代码:
wp=2*pi*200; %技术指标
ws=2*pi*800;
Rp=2;
As=20;
[N1,wc1]=buttord(wp,ws,Rp,As,'s') %巴特沃斯滤波器
[B,A]=butter(N1,wc1,'s')
k=0:511; %意义何在?就是为了采样而已,把一段曲线化成几段折线表示
fk=0:1000/512:1000;
wk=2*pi*fk;
Hk=freqs(B,A,wk); %求解滤波器的频率响应
plot(fk/1000,abs (Hk)); %绘图,fk除以1000的意义是把横轴频率归一化
hold on
wp=2*pi*200; %技术指标
ws=2*pi*700;
Rp=2;
As=20;
[N2,wc2]=cheb1ord(wp,ws,Rp,As,'s') %切比雪夫滤波器
[B,A]=cheby1(N2,Rp,wc2,'s')
k=0:511;
fk=0:1000/512:1000;
wk=2*pi*fk;
Hk1=freqs(B,A,wk);
plot (fk/1000,abs (Hk1),'r');
grid on
hold on
wp=2*pi*200; %技术指标
ws=2*pi*500;
Rp=2;
As=20;
[N3,wc3]=ellipord(wp,ws,Rp,As,'s'); %椭圆滤波器
[B,A]=ellip(N3,Rp,As,wc3,'s');
k=0:511;
fk=0:1000/512:1000;
wk=2*pi*fk;
Hk2=freqs (B,A,wk);
plot (fk/1000,abs (Hk2),'g');
title('幅频特性');
xlabel('频率/kHz');
ylabel('幅度');
legend('巴特沃斯','切比雪夫','椭圆');
运行结果:
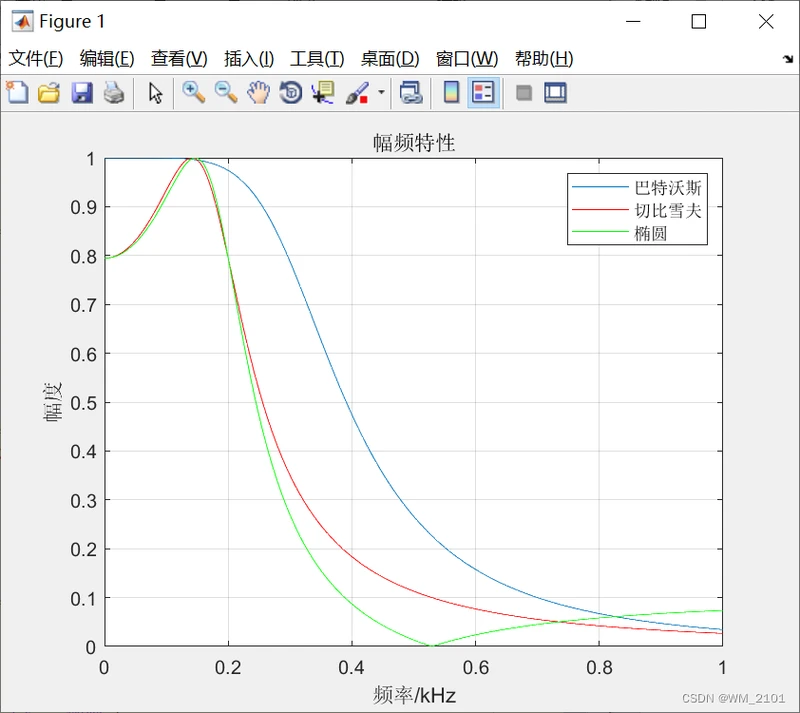
由结果分析可知:
在相同阶数、相同通带最大衰减、阻带最小衰减要求下,巴特沃斯滤波器的过渡带最宽;椭圆滤波器过渡带最窄;切比雪夫滤波器的过渡带介于巴特沃斯滤波器和椭圆滤波器之间。
通带截至频率相同时,阻带截止频率,巴特沃斯滤波器的截止频率最大,椭圆滤波器的截止频率最小。
7、不同类型的模拟滤波器的比较(阻带衰减)
设定相同的低通滤波器阶次、通带衰减、通带和阻带截止频率,利用MATLAB设计函数分别设计出相应的模拟巴特沃斯、切比雪夫(任选I型或II型)、椭圆滤波器(通过尝试不同的阻带衰减数值,使得各类滤波器的阶次相同),画出所设计滤波器的幅频特性曲线,比较不同类型滤波器阻带衰减的差异。
代码:
%% 代码:
%% 巴特沃斯
wp=2*pi*5000; %技术指标
ws=2*pi*12000;
Rp=2;
As=30;
[N,wc]=buttord(wp,ws,Rp,As,'s') %巴特沃斯滤波器
[B,A]=butter(N,wc,'s');
k=0:999; %意义何在?将曲线化成1000段折线画出来
fk=0:14000/1000:14000;
wk=2*pi*fk;
Hk=freqs(B,A,wk);
subplot(3,1,1);
plot(fk/1000,20*log10(abs(Hk))); %绘图?与教材程序一个方法
grid on
xlabel('频率(kHz)');
ylabel('幅度(dB)');
title('巴特沃斯');
%% 切比雪夫I型
wp=2*pi*5000; %技术指标
ws=pi*15000;
Rp=2;
As=60;
[N1,wp1]=cheb1ord(wp,ws,Rp,As,'s') %切比雪夫I型滤波器
[B1,A1]=cheby1(N1,Rp,wp1,'s');
fk=0:12000/1000:12000;
wk=2*pi*fk;
Hk=freqs(B1,A1,wk);
subplot(3,1,2);
plot(fk/1000,20*log10(abs(Hk)));
grid on
xlabel('频率(kHz)');
ylabel('幅度(dB)');
title('切比雪夫I型');
%% 椭圆模拟低通滤波器
wp=2*pi*5000; %技术指标
ws=pi*15000;
Rp=2;
As=75;
[N,wpo]=ellipord(wp,ws,Rp,As,'s') %椭圆滤波器
[B,A]=ellip(N,Rp,As,wpo,'s');
k=0:999;
fk=0:14000/1000:14000;
wk=2*pi*fk;
Hk=freqs(B,A,wk);
subplot(3,1,3);
plot(fk/1000,20*log10(abs(Hk)));
grid on
xlabel('频率(kHz)');
ylabel('幅度(dB)');
title('椭圆模拟低通滤波器');
运行结果:
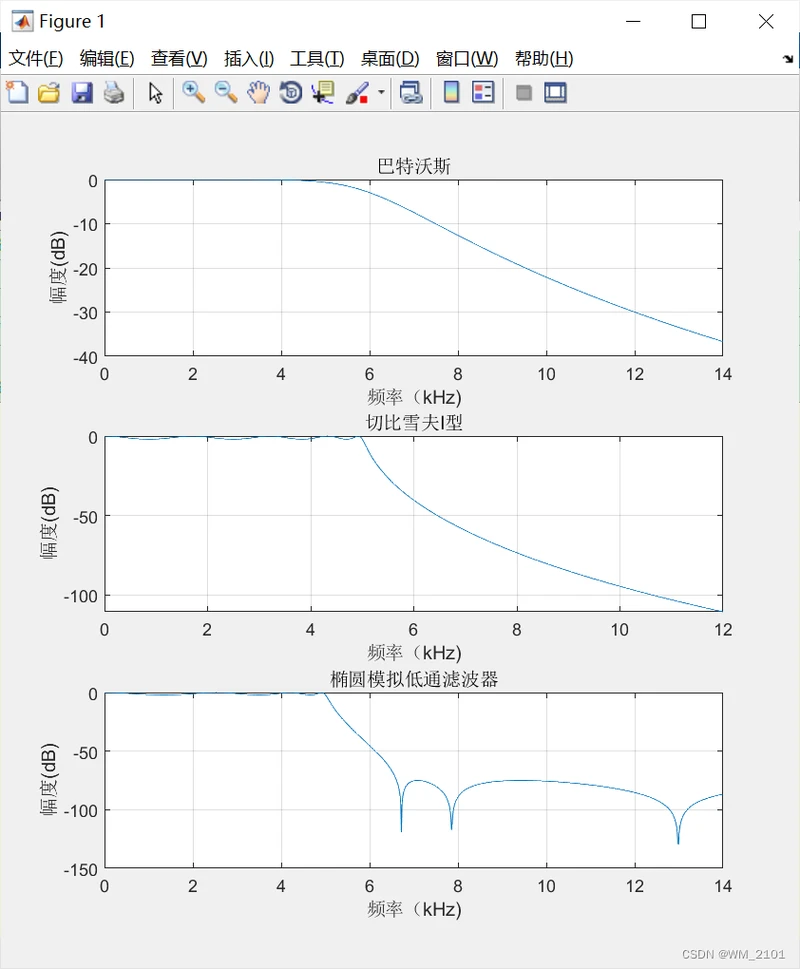
分析:
1)巴特沃斯的阻带衰减最小;
2)椭圆滤波器的阻带衰减最大;
3)两种类型的切比雪夫滤波器的阻带衰减介于巴特沃斯滤波器和椭圆滤波器之间。
8、不同模拟滤波器的比较(总结)
总结4-7题的设计分析结果,讨论不同类型低通选频滤波器的特点。在滤波器技术指标相同的情况下,哪种类型模拟滤波器的阶次最低?
1)不同类型低通选频滤波器的特点:
巴特沃斯滤波器:
幅频特性单调下降,在靠近通带截止频率处,幅度下降很多。所以为了使通带内的衰减足够小,需要的阶次N较高。
切比雪夫滤波器:
Ⅰ型滤波器通带内等波纹幅频特性,过渡带、阻带单调下降;
Ⅱ型滤波器阻带内等波纹幅频特性,通带、过渡带单调下降。
同样的通带衰减,其所需阶数N较巴特沃斯滤波器要小。巴特沃斯和切比雪夫滤波器在大约四分之三的通带上非常接近线性相位特性。
椭圆滤波器:
通带、阻带内均等波纹幅频特性,过渡带单调下降。
对于给定的阶数和给定的波纹要求,椭圆滤波器能获得较其它滤波器更窄的过渡带宽。通带和阻带内波纹固定时,阶数越高,过渡带越窄;阶数固定,通带和阻带纹波越小,过渡带越宽。椭圆滤波器仅在大约半个通带上非常接近线性相位特性。
贝塞尔滤波器:
在通带内逼近线性相位特性。
2)在相同指标要求下,椭圆滤波器所需的阶次N最低,切比雪夫次之,巴特沃斯最高。
