首先,对于简单的凸函数的相加,凸函数求最大值,都是能够保证函数的凸性的,相比而言,复合函数就较为复杂了。
给定函数
f
:
R
k
→
R
f:R^k\rightarrow R
f:Rk→R以及
g
:
R
n
→
R
k
g:R^n\rightarrow R^k
g:Rn→Rk,我们定义复合函数
f
=
h
⋅
g
:
R
n
→
R
f=h\cdot g:R^n\rightarrow R
f=h⋅g:Rn→R为:
f
(
x
)
=
h
(
g
(
x
)
)
,
d
o
m
f
=
{
x
∈
d
o
m
g
∣
g
(
x
)
∈
d
o
m
h
}
f(x)=h(g(x)), dom f=\{x\in dom g|g(x)\in dom h\}
f(x)=h(g(x)),domf={x∈domg∣g(x)∈domh}
我们考虑当复合函数保持凸性或者凹性时,两个函数分别应该满足什么样的条件。
标量
\textbf\color{orange}{标量}
标量
对标量而言,上述方程我们直接求二阶导进行判定即可,复合函数的二阶倒数为
f
′
′
(
x
)
=
h
′
′
(
g
(
x
)
)
g
′
(
x
)
2
+
h
′
(
g
(
x
)
)
g
′
′
(
x
)
f''(x)=h''(g(x))g'(x)^2+h'(g(x))g''(x)
f′′(x)=h′′(g(x))g′(x)2+h′(g(x))g′′(x)
如果这个值恒大与0,那么函数就满足凸函数的性质,那么我们有以下结论:

Genaral Case \textbf\color{orange}{Genaral Case} Genaral Case
注意上述结论成立的条件:
g
,
h
g,h
g,h都是二次可微的,而且他们的定义域都是
R
R
R。事实上,对于更一般的情况,
n
>
1
n>1
n>1,不再局限于一维空间,也不再假设
g
,
h
g,h
g,h可微或者
d
o
m
g
∈
R
n
,
d
o
m
h
∈
R
dom g\in R^n,dom h\in R
domg∈Rn,domh∈R,一些相似的复合规则仍然成立。

这里需要用到函数的拓展,将函数的定义域拓展到整个
R
n
R^n
Rn空间显然会使得我们的分析更加简单。
h
~
\widetilde h
h
即
h
h
h函数的拓展,如果点
g
(
x
)
g(x)
g(x)不在定义域中,而且
h
h
h是凸函数,那么对其赋值为
∞
\infty
∞(保持
h
h
h的凸性)。反之如果
h
h
h是凹函数,那么对其赋值为
−
∞
-\infty
−∞。可以看到,这里和上面唯一的不同就在于,我们对
h
h
h函数进行了扩展,使其在整个空间内非增或者非减。
函数扩展的注意事项
\textbf\color{grey}{函数扩展的注意事项}
函数扩展的注意事项
需要注意的是,函数的扩展非常重要,我们需要
h
~
\widetilde h
h
在整个空间内有单调性,而不只是在定义域内
考虑如下函数:
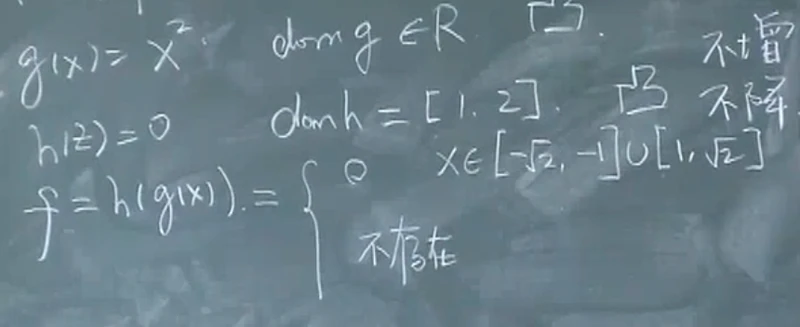
显然在定义域内
h
h
h是不增不降的,既是凸函数也是凹函数,如果我们根据上述条件,只考虑
h
~
\widetilde h
h
在定义域内的单调性的话,显然复合函数即可以使用第一条性质也可以使用第二条性质,但是实际上,这个函数既不是凸函数,也不是凹函数,因为他连定义域都不是凸的:

而且当我们对他进行函数扩展时可以发现无论是进行凸扩展还是凹扩展,他的
h
~
\widetilde h
h
始终是不具有单调性的,因此该函数既没有凸性,也没有凹性。Again,
h
~
\widetilde h
h
必须在整个空间内具有单调性。
Simple Example \textbf\color{orange}{Simple Example} Simple Example
- 函数 h ( x ) = log x h(x)=\log x h(x)=logx,定义域为 d o m h = R + + dom h=R_{++} domh=R++,其在 x ≤ 0 x\leq0 x≤0处扩展为 − ∞ -\infty −∞,可以得到 h ~ \widetilde h h 非减,且 h ( x ) h(x) h(x)为凹函数。
- 函数 h ( x ) = x 1 / 2 h(x)=x^{1/2} h(x)=x1/2,定义域为 d o m h = R + dom h=R_{+} domh=R+,其在 x < 0 x<0 x<0处扩展为 − ∞ -\infty −∞,可以得到 h ~ \widetilde h h 非减,且 h ( x ) h(x) h(x)为凹函数。
- 函数 h ( x ) = x 3 / 2 h(x)=x^{3/2} h(x)=x3/2,定义域为 d o m h = R + dom h=R_{+} domh=R+,如果其在 x < 0 x<0 x<0处扩展为 ∞ \infty ∞,可以得到 h ( x ) h(x) h(x)为凹函数,但是不满足 h ~ \widetilde h h 非减的条件,
- 函数 h ( x ) = x 3 / 2 h(x)=x^{3/2} h(x)=x3/2,定义域为 d o m h = R + dom h=R_{+} domh=R+,如果其在 x < 0 x<0 x<0处扩展为 0 0 0,可以得到 h ( x ) h(x) h(x)为凹函数,而且满足 h ~ \widetilde h h 非减的条件,
简单的复合结论
\textbf\color{orange}{简单的复合结论}
简单的复合结论

