前面一篇提到二进制队列实现了 N位二进制的补码,那么我们来实现布思算法。
关于BinaryQueue:https://www.cnblogs.com/XT-xutao/p/10050518.html
先来思考:我们这样实现二进制乘法呢?
对于无符号整数,是可以转化为加法的:
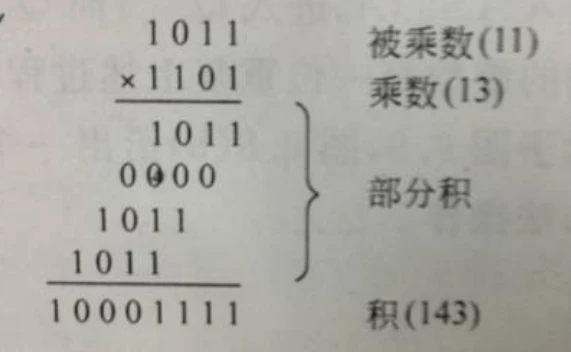
那么补码形式呢?好像一些也是可以用上面这种转化为加法的:
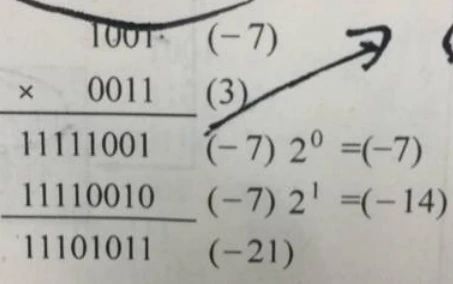
上面被乘数-7是小于0的,但是乘数为负的时候好像就不能工作了,因为不能正确地得出部分积。
怎么办呢?
还有一种方法: 就是在乘之前先判断符号,如果异号,则结果为负,用他们的绝对值形式乘就可以了,最后加符号就行。
但是,这种方法似乎太麻烦了,我们更偏向于——布思算法(BOOTH)
布思算法是基于: 2^n+2^n-1......2^n-k = 2^(n+1) - 2^(n-k)
它有两大优点:
1.避免了如上的那种复杂操作。
2.减少了不必要的加法,节约了时间。
那么在计算机底层是怎么实现的呢?
可以用几个寄存器搞定:
A:附加寄存器,初始化0
Q:乘数寄存器
M:被乘数寄存器
Q0:乘数的最低位,初始化0
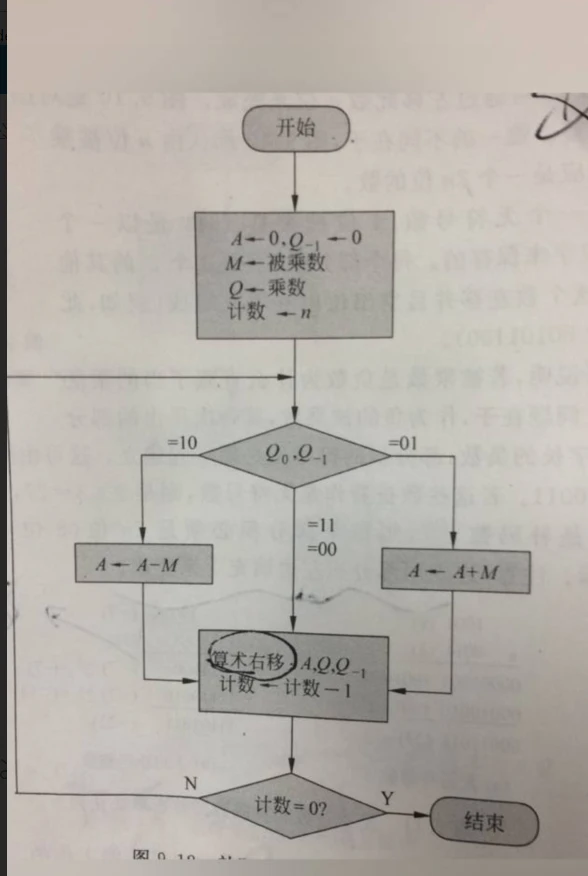
根据流程图就可以实现了。最后的结果是AQ寄存器里的值。
更新:前面讲那个BinaryQueue方法不好,直接用字符串形式的二进制表示更简单:
1 public String multiply(String Q,String M){
2 char Q0 = '0';
3 String A = get01(Q.length(),"0");
4 for (int i=0;i<Q.length();i++){
5 String QQ0 =Q.charAt(Q.length()-1)+""+Q0;//不能把两个char字符放在一起,会变成加
6 System.out.println(QQ0);
7 if (QQ0.equals("10")){
8 A=substract(A,M).substring(1);
9 }
10 else if (QQ0.equals("01")){
11 A=add(A,M).substring(1);
12 }
13 String temp = shiftRight(A+Q+Q0);
14 A=temp.substring(0,A.length());
15 Q = temp.substring(A.length(),2*A.length());
16 Q0 = temp.charAt(temp.length()-1);
17 }
18 return A+Q;
19 }
