一、什么是RSA
RSA公开密钥密码体制是一种使用不同的加密密钥与解密密钥,“由已知加密密钥推导出解密密钥在计算上是不可行的”密码体制。[百度百科]
RSA是一种非对称密码也就是公钥密码,顾名思义就是加密和解密使用的密钥不同,其中一个称为公钥,即可以公开的密钥;另一个称为私钥,即必须持有者保密的密钥;而且由公钥不可能计算出私钥。
任何人都可以生成自己的私钥和公钥,把公钥公开,把私钥自己保管。当别人想把加密文件的密码发送给我的时候,就可以用我的公钥对密码进行加密,然后发给我,然后我用我的私钥解密就可以拿到加密文件的密码。因为只有我拥有我的私钥,所以除了我之外的其他人,是不可能获得加密文件密码的。
如此一来,公钥密码就解决了密钥分发问题,也保障了很好地安全性。
二、数学基础
1.整除
如果a整除b,记为a|b。
若c=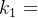 a+
a+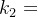 b,e|a,且e|b,则e|c。
b,e|a,且e|b,则e|c。
2.最大公因子
所有同时整除a和b的整数中,最大的那个,称为a和b的最大公因子,记为(a,b)。
根据这个结论,对任意正整数a和b,首先a一定可以表示成a=kb+c,0≤c<b也就是说k=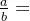 ,a mod b =c。
,a mod b =c。
其次(a,b)=(b,c),也就是说, a和b的最大公因子,b和c的最大公因子,是相同的。
欧几里得算法(求最大公因子)
def gcd(a, b):
if b == 0:
return a
return gcd(b, a % b)扩展欧几里得算法(对于任意两个整数 a, b,必存在整数 x, y,使得 xa + yb = gcd(a,b) 成立,求出整数解 x, y,可以得到 gcd(a,b))
def egcd(a, b):
if b == 0:
return a, 1, 0
gcd, x, y = egcd(b, a % b)
return gcd, y, x - a / b * y3.互素
最大公因子的最小可能取值是1,当(a,b)=1,即a和b的最大公因子为1时,我们称a和b互素。
4.乘法逆元
当(a,b)=1时,有时候我们很希望求得一个数k,0≤k<b,使ka mod b =1,这样的数我们称为a的乘法逆元,
起始这看起来就像是在0到b-1这些整数中找到的倒数一样。那怎么找到这样的数呢?
扩展欧几里得算法可以帮我们解决这个问题。
由于(a,b)=1,根据扩展欧几里得算法,可求得两个系数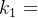 和
和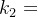 ,使得
,使得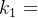 a+
a+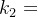 b=(a,b)=1,所以有
b=(a,b)=1,所以有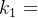 a=-
a=-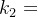 b+1,所以
b+1,所以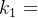 a mod b =1,所以(
a mod b =1,所以(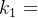 mod b)a mod b =1,而0≤(
mod b)a mod b =1,而0≤(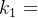 mod b)<b,所以(
mod b)<b,所以(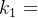 1 mod b)就是我们想要的那个乘法逆元。
1 mod b)就是我们想要的那个乘法逆元。
5.欧拉函数
对任意一个正整数,在到的这个整数里,显然有些和是互素的,而有些和是不互素的,那些和互素的整数的数量就是n的欧拉函数,记作φ(n)。
特殊的,φ(1)=1。
如果n是质数,则φ(n)=n-1。因为质数与小于它的每一个数,都构成互质关系。比如5与1、2、3、4都构成互质关系。
如果n是质数的某一个次方,即 n = p^k (p为质数,k为大于等于1的整数),则φ(p^k)=p^k-p^(k-1)
如果n可以分解成两个互质的整数之积,即n=p1p2,则φ(n)=φ(p1p2)=φ(p1)φ(p2)
6.欧拉定理(RSA直接数学基础)
当(a,n)=1时,a^φ(n)≡1 (mod n)
推论
a^(φ(n)+1)≡a (mod n)
三、RSA计算
C=M^E mod N
M=C^D mod N (C代表密文,M代表明文)
N=p*q (p q为随机生成的两个质数)
E为随机生成的质数(较p q小)
E*D mod φ(n) =1 (由欧拉定理的推论得出,本文中没有详写),所以
D = gmpy2.invert(E,(p-1)*(q-1))至此,RSA密码的加解密都可计算。
四、例题
已知:
p = 262248800182277040650192055439906580479
q = 262854994239322828547925595487519915551
e = 65533
c = 27565231154623519221597938803435789010285480123476977081867877272451638645710求m。
import gmpy2
import libnum
from Crypto.Util.number import *
#from binascii import a2b_hex,b2a_hex
p = 262248800182277040650192055439906580479
q = 262854994239322828547925595487519915551
e = 65533
n = p*q
d = gmpy2.invert(e,(p-1)*(q-1))
#print(d)
#c = pow(int(b2a_hex(flag),16),e,n)
#print c
c = 27565231154623519221597938803435789010285480123476977081867877272451638645710
# c = m^e % n
# m = c^d % n
m = pow(c,d,n)
print(m)
#m=2077392566271395359695912870032509