1. 合式公式
• 我们会逐渐进入命题逻辑的形式讨论:我们对命题只注意其命题形式,对联结词只注意其逻辑意义。
• 命题逻辑合式公式的定义给出了命题逻辑研究的对象范围。所有符合定义的合式公式构成合式公式空间,它可被视为命题逻辑的符号化语言。语言的结构包括符号表、语法规则(即合适公式定义)和语义(也即真值)。
• 定义:符号化语言 Lp 的符号表包括
− 小写英文字母:p, q, r, … 称为命题变量(或原子变量)。所有可能出现的命题变量的集合记为 Var;
− 命题联结词:包括五个联结词 ¬, ∧, ∨, →, ↔;
− 助记符:包括左右两个小括号 (, )。
• 定义:命题逻辑的合式公式 (wff, well‐formed formula)
• 一个命题变量 p 是一个 wff;• 若 A 是 wff,则 (¬A) 也是 wff;
• 若 A, B 是 wff,则 (A∧B), (A∨B), (A→B), (A↔B) 也是wff;
• 当且仅当有限次使用上述规则得到的才是 wff。
• 定义:联结词的优先级
− 规定联结词的运算优先级从高到底为:¬ ∧ ∨ → ↔− 书写公式时,在不引起误解的情况下,可以省略部分小括号。
| » 例:(p→(q∧r)) 可写成 p→(q∧r), 或 p→q∧r |
• 定义:真值赋值函数
− 具有形式 t:Var→{0,1} 的函数,它为变量表 Var 中的每个命题变量 p∈Var 指派一个真值 (1/0)。
| » 例:Var = {p, q},可以定义赋值函数t如下: t(p)=0,t(q)=1 |
− 在含有 n 个命题变量的 Var上,可以定义的赋值函数有 2n 个,称为对此 n个命题变量的 2n 个解释。
| » 例:对 Var={p, q},可以有 2n=4个不同的解释: t0(p)=0,t0(q)=0; t1(p)=0,t1(q)=1; t2(p)=1,t2(q)=0; t3(p)=1,t3(q)=1; |
− 设下述 A, B, C 都是合式公式。给定一个真值赋值函数 t : Var → {0,1} ,则任意公式 A 在 t 下的真值 T(A):
− 若 A 是命题变量形式 p,则 T(A)=T(p);
− 若 A 具有形式 (¬B),则 T(A)=1 iff T(B)=0;
− 若 A 具有形式 (B∧C),则 T(A)=1 iff T(B)=1且T(C)=1;
− 若 A 具有形式 (B∨C),则 T(A)=0 iff T(B)=0且T(C)=0;
− 若 A 具有形式 (B→C),则 T(A)=0 iff T(B)=1且T(C)=0;
− 若 A 具有形式 (B↔C),则 T(A)=1 iff T(B)=T(C);
注意到 Var中包含了本次计算涉及的所有命题变量。上述对A的真值T(A)的定义是一个递归定义,对T(A)的计算是一个递归过程,所需步数等于利用wff定义构造A的归纳步数。由于A的构造步数是有限的,所以T(A)的递归计算将在有限步数后终止。
• 定义:合式公式的真值表
− 可以采用真值表的方法对 A 的逻辑意义作直观的描述:对任何一个可能的赋值函数(解释)ti,计算出相应 T(A),称为 A 在 ti下的真值。将所有的 2n 个(n=|Var|) 不同的解释及 A 在各个解释下的真值用表格的形式列明,称为公式A 的真值表。
• 定义:合式公式的真值表
− 例: (p∧(p∨q))
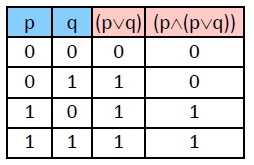
在每个解释下,计算 (p∨q) 的真值,再以 p 的真值和 (p∨q) 的真值作合取,依合取的定义得到最右栏的真值.
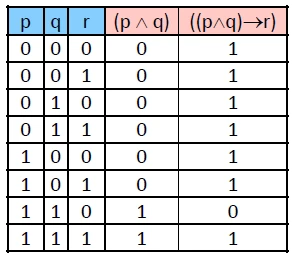
− 例:((p∧q)→r)
− 在所有真值赋值函数下真值都为1的合式公式称为重言式(或永真式)。
− 能在某一真值赋值函数下取得真值1的合式公式称为可满足式。
− 在所有真值赋值函数下真值都为0的合式公式称为矛盾式(或永假式)。
重言式在任何解释下都为真,故其真值表对应的最右列全是1;可满足式至少在一个解释下为真,故该列至少有一个是1; 矛盾式在任何解释下都为假,故该列全是0
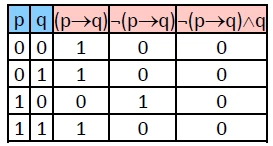
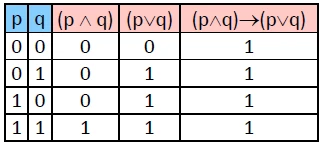
− 例: (p∧q)→(p∨q) 是重言式
− 例: ¬(p→q)∧q 是矛盾式