线索二叉树的应用数据结构

前面说完了二叉树的基本知识后，我们紧追其后来分享几种特殊又很重要的二叉树，这几种特殊的二叉树在平时的刷题中也是重点和难点，是树这一数据结构的最高层次。今天我们开始来看一看第一种吧——线索二叉树。

1.概念：为了区分二叉树的左孩子指针和右孩子指针是否为空，或者是否指向前驱节点或后继节点，我们将节点的结构改成5个域，在原二叉树的基础上添加左标志域Ltag和右标志域Rtag，他们是两个int型的数据域。

如果节点有左孩子，那么Lchild依然指向他的左孩子，否则指向遍历序列中他的前驱节点。

如果节点有右孩子，那么Rchild依然指向他的左孩子，否则指向遍历序列中他的后继节点。

Ltag和Rtag的定义如下:
Ltag : 等于0时，Lchild域指示节点的左孩子;等于1时，Lchild指示节点的遍历前驱。
Rtag : 等于0时，Rchild域指示节点的右孩子;等于1时，Rchild指示节点的遍历后继。

注意一下小概念：线索是指向前驱和后继节点的指针。

2.线索二叉树与二叉树的存储结构比较

线索二叉树：

typedef struct BiThrNode

{ char data;

struct BiThrNode *lchild, *rchild;

int LTag;

int RTag;

}BiThrNode,*BiThrTree;

普通二叉树：

typedef struct BiTNode

{ char data;

struct BiTNode* lchild,*rchild;

}BiTNode,*BiTree;

划重点：相较于二叉树添加了LTag和RTag标记，当标记值为0时代表该结点有儿子结点，标记值为1时其lchild指针指向上一个结点，rchild指针指向下一个结点（指中序遍历的前结点或后结点）。建立线索二叉树的目的是最大化利用空指针，构建二叉树中许多结点并没有左右儿子结点，因此他们的lchild和rchild指针均没有被利用。我们将没有利用的指针指向该结点的前驱或后继成为线索，对二叉树以某种次序遍历使其变为线索二叉树的过程称作线索化。

3.创建线索二叉树（这里举例用先序遍历创建，其他遍历方式类推）：

void PreCreateBiTree(BiThrTree &T)
{
   char ch;
   cin>>ch;
   if (ch=='#')
   {
       T=NULL;
   }
   else
   {
       T=new BiThrNode;//创建新节点
       if(!T)

cout<<"error!"<<endl;
       (T)->data=ch;
       PreCreateBiTree((T)->lchild);
       PreCreateBiTree((T)->rchild);
   }
}
4.用中序遍历的方法来使二叉树线索化

实现：
①pre是全局变量，始终指向刚刚问过的结点（当前结点的前一个结点）
②从树根开始，先遍历到最深的左孩子结点，如果该结点没有左孩子，将LTag置为1做标记，令其lchild指针指向pre前驱，否则将LTag置为0，其lchild指针仍然指向左孩子结点。
③如果前驱没有右孩子结点，将前驱的RTag置为1做标记，令其rchild指针指向当前结点p，保持pre=p继续遍历，接着遍历右子树。

BiThrTree pre;
void InThreading(BiThrTree p)
{
   if (p)//如果p不为空
   {
       InThreading(p->lchild);//进入当前结点的最深左子树
       if (!p->lchild)//没有左孩子
       {
           p->LTag=1;
           p->lchild=pre;
       }
       else p->LTag=0;
       if (!pre->rchild)//没有右孩子
       {
           pre->RTag=1;
           pre->rchild=p;
       }
       else pre->RTag=0;
       pre=p;
       InThreading(p->rchild);
   }
}

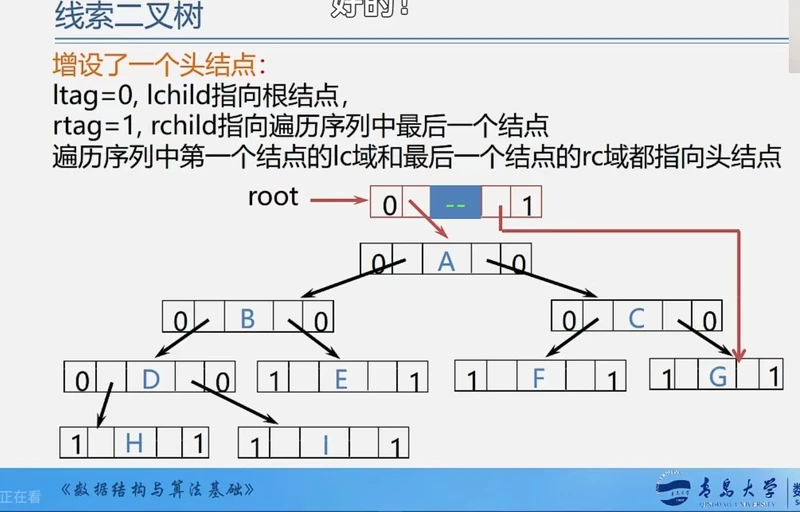
5.优化方法：加上头结点

功能：为二叉树添加头结点后中序线索化
实现：
①创建头结点，申请内存空间，将LTag置为0，左孩子结点指向二叉树的根结点。将RTag置为1，初始化时默认右孩子指针指向自己，如果树为空，左孩子指针也指向自己。
②若树非空则开始中序线索化，将左孩子指向二叉树根结点，pre前置指针指向头结点，开始中序线索化。
③中序线索化结束，pre指针指向中序遍历最后一个结点，将最后一个结点的右孩子指针指向头结点，标记RTag为1。
④最后让头结点的右孩子指针指向最后一个结点，连成双向的二叉链表
void InOrderThreading(BiThrTree &Thrt,BiThrTree T)
{
   Thrt=new BiThrNode;
   Thrt->LTag=0;
   Thrt->RTag=1;
   Thrt->rchild=Thrt;
   if(!T) Thrt->lchild=Thrt;
   else
   {
       Thrt->lchild=T;
       pre=Thrt;
       InThreading(T);
       pre->rchild=Thrt;
       pre->RTag=1;
       Thrt->rchild=pre;
   }
}

插入王卓老师网课的图片加强理解

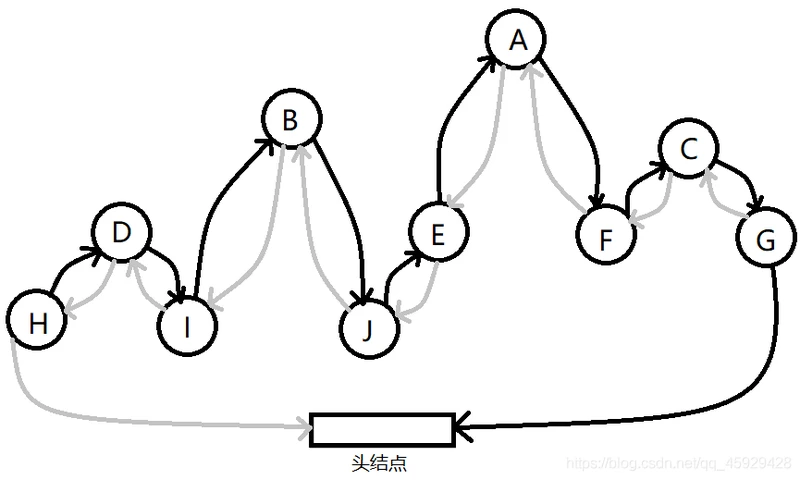
6.中序遍历二叉树

功能：中序遍历线索二叉树
实现：
①令p=T->lchild，将p指向树根结点，循环遍历当p=T时说明回到了头结点即遍历结束。
②当p！=T时，首先移动到最深的左儿子结点，输出数据。接着判断RTag若为1，则说明p的rchild指针指向中序遍历的下一个结点，于是按照右线索访问后继结点
③p=p->rchild即转向p的右子树继续遍历，直到回到头结点结束。
void InOrderTraverse_Thr(BiThrTree T)
{
   BiThrTree p;
   p=T->lchild;
   while (p!=T)
   {
       while (p->LTag==0) p=p->lchild;
       cout<<p->data;
       while (p->RTag==1&&p->rchild!=T)
       {
           p=p->rchild;
           cout<<p->data;
       }
       p=p->rchild;
   }
}

7.中序线索二叉树寻找遍历的首节点

按照这样的访问次序，首先访问的是树的最左下端，即沿着左孩子链走到最下端，找到第一个没有左孩子的节点(Ltag == 1)（简单的来说就是找最左下角的那个结点）

BiTree InFirst(BiTree bt)
{
   BiTree p = bt;
   if(p == NULL)
   return(NULL);
   //因为是中序遍历，所以最开始的节点一定是最左边的
   while(p->Ltag == 0)
{ p = p->Lchild;}
   return(p);
}

8.中序线索二叉树寻找节点的直接后继

对于传进来的参数节点p，如果p没有右孩子那么直接可以获得他的后继节点，如果p有右子树，那么他的后继节点应该是p右子树中第一个遍历到的节点，有中序遍历我们可以知道，p的后继节点就是他右子树的最左下端第一个没有左孩子的节点

BiTree InNext(BiTree p)
{
   BiTree next,q;
   if(p->Rtag == 1)
   {
       next = p->Rchlid;//直接利用线索
   }
   //右边的子树查找后继节点有问题
   else{
       //在p的右子树中查找最左下端的节点
       for(q = p->Rchlid; q->Ltag == 0; q = q->Lchild);
       next = q;

   }
   return(next);
}
9.遍历中序线索二叉树

利用上述的InFirst和InNext函数进行遍历

BiTree TinOrder(BiTree root)

{

BiTree p;

p = InFirst(root);

while(p != NULL)

{ printf("%c",p->data);

p = InNext(p);

}

10.这里有一个完整的代码,来表示从建立二叉树到线索化,遍历的全过程

代码:

#include <stdio.h>
#include <stdlib.h>
//函数状态结果代码
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
//Status是函数的类型，其值是函数结果状态代码
typedef int Status;
typedef char TElemType;
typedef enum { Link, Thread } PointerTag;//枚举值为0或1
typedef struct BiThrNode {
TElemType data;
struct BiThrNode* lchild, * rchild;
PointerTag LTag;
PointerTag RTag;
}BiThrNode, * BiThrTree;

//线索二叉树初始化
Status CreateBiThrNode(BiThrTree* B) {
char ch;
scanf_s("%c", &ch);
if (ch == '#') *B = NULL;
else {
if (!((*B) = (BiThrNode*)malloc(sizeof(BiThrNode)))) exit(OVERFLOW);//创建不成功不会执行下面
(*B)->data = ch;
(*B)->LTag = Link;
(*B)->RTag = Link;
CreateBiThrNode(&(*B)->lchild);
CreateBiThrNode(&(*B)->rchild);
}
return OK;
}

//线索二叉树线索化
void InThreading(BiThrTree B, BiThrTree* pre) {
if (!B) return;

InThreading(B->lchild, pre);

if (!B->lchild) {
B->LTag = Thread;
B->lchild = *pre;
}

if (!(*pre)->rchild) {
(*pre)->RTag = Thread;
(*pre)->rchild = B;
}

*pre = B;
InThreading(B->rchild, pre);
}

//为线索二叉树添加头结点，使之可以双向操作
Status InOrderThreading(BiThrTree* Thrt, BiThrTree T) {
if (!(*Thrt = (BiThrTree)malloc(sizeof(BiThrNode)))) exit(OVERFLOW);
(*Thrt)->LTag = Link;
(*Thrt)->RTag = Thread;
(*Thrt)->rchild = (*Thrt);
if (!T) {
(*Thrt)->lchild = (*Thrt);
return OK; //若根结点不存在,则该二叉树为空,让该头结点指向自身.
}
BiThrTree pre;
//令头结点的左指针指向根结点
pre = (*Thrt);
(*Thrt)->lchild = T;
//开始递归输入线索化
InThreading(T, &pre);
//此时结束了最后一个结点的线索化了,下面的代码把头结点的后继指向了最后一个结点.
//并把最后一个结点的后继也指向头结点,此时树成为了一个类似双向链表的循环.
pre->rchild = *Thrt;
pre->RTag = Thread;
(*Thrt)->rchild = pre;
return OK;
}

//非递归遍历线索二叉树
Status InOrderTraverse(BiThrTree T) {
BiThrNode* p = T->lchild;
while (p != T) {
while (p->LTag == Link) p = p->lchild; //走向左子树的尽头
printf("%c", p->data);
while (p->RTag == Thread && p->rchild != T) { //访问该结点的后续结点
p = p->rchild;
printf("%c", p->data);
}
p = p->rchild;
}
return OK;
}

int main() {
BiThrTree B, T;
CreateBiThrNode(&B);
InOrderThreading(&T, B);
printf("中序遍历二叉树的结果为：");
InOrderTraverse(T);
printf("\n");
}

程序执行图:

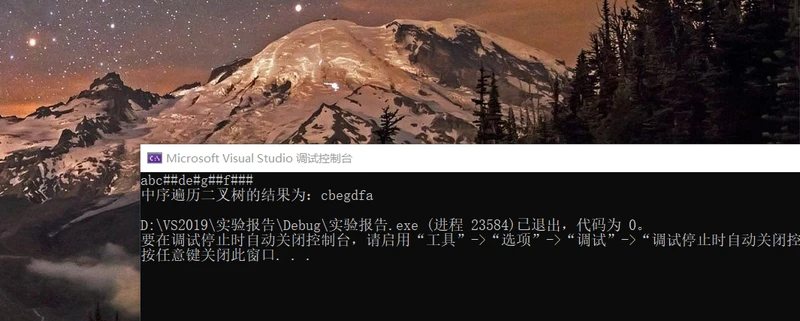
本贴为博主亲手整理。如有错误，请评论区指出，一起进步。谢谢大家的浏览.

知秋君

相关推荐