直方图与密度图的绘制方法

直方图

基础实现

hist()函数

扩展

色彩映射

双变量直方图

拟合分布曲线

密度图

基础实现

kdeplot()函数

扩展

多变量密度图

分组密度图

总结

直方图

直方图是一种常用的数据可视化工具，用于展示数据的分布情况。它将数据划分为若干个等宽的区间（也称为箱子或柱形），并计算每个区间内数据的频数或频率，具体应用可参考：直方图在照片中的应用。直方图的作用如下：

揭示数据分布：直方图可帮助我们了解数据的分布形态和特征。通过观察直方图的形状、峰值、对称性等信息，我们可以获得关于数据集的直观认识。例如，直方图可以显示数据是集中在某个区间还是分散在整个范围内，是否存在异常值或离群点等。
发现数据的统计特征：通过直方图，我们可以观察数据的中心趋势、变异程度和偏斜程度等统计特征。例如，直方图的峰值位置可以反映数据的众数，直方图的宽度可以表示数据的分散程度。直方图还可以用于检测数据的偏斜性，例如正态分布通常具有对称的直方图。
比较不同数据集：直方图可以用于比较不同数据集之间的分布差异。通过将多个直方图放在一起进行观察，我们可以发现数据之间的相似性或差异性。这对于数据分析、探索性数据分析以及进行假设检验等都非常有用。
探索异常值和离群点：直方图可以帮助我们发现数据中的异常值或离群点。异常值通常表现为在直方图中与其他数据点明显不同的极端值。通过观察直方图，我们可以识别这些异常值，并进一步进行数据清洗或分析。

基础实现

当使用Matplotlib绘制直方图时，你可以使用 matplotlib.pyplot.hist() 函数。

import numpy as np
import matplotlib.pyplot as plt

# 生成随机数据
np.random.seed(0)
data = np.random.randn(1000)  # 生成1000个服从标准正态分布的随机数

# 绘制直方图
plt.hist(data, bins=30, edgecolor='black')  # 使用30个柱形，并设置柱形边界颜色为黑色
plt.xlabel('Value')  # x轴标签
plt.ylabel('Frequency')  # y轴标签
plt.title('Histogram of Random Data')  # 图表标题
plt.grid(False)  # 显示网格线
plt.show()  # 显示图表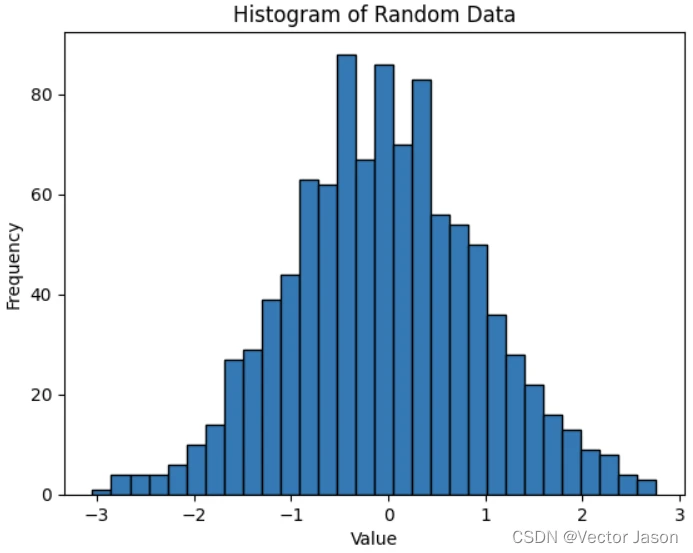

hist()函数

定义：

matplotlib.pyplot.hist(x, bins=None, range=None, density=False, weights=None, cumulative=False, bottom=None, histtype='bar', align='mid', orientation='vertical', rwidth=None, log=False, color=None, label=None, stacked=False, \*, data=None, \*\*kwargs)

参数:

x : 待可视化处理的数据集
bins : 统计的区间分布划分，指定绘制柱形图的总个数；
range : 显示的区间
density : 显示概率密度，默认为false
histtype : 可选{‘bar’, ‘barstacked’, ‘step’, ‘stepfilled’}之一，默认为bar，推荐使用默认配置，step使用的是梯状，stepfilled则会对梯状内部进行填充，效果与bar类似
align : 可选{‘left’, ‘mid’, ‘right’}之一，默认为’mid’，控制柱状图的水平分布，left或者right，会有部分空白区域，推荐使用默认
log : 默认为False，y坐标轴是否选择指数刻度，在数据分布的范围较大的时候，可以通过log指数刻度来缩小显示的范围。
stacked : 默认为False，是否为堆积状图

扩展

色彩映射

hist函数返回值有3个，分别是：

频数数组（histogram）：这是一个包含每个区间内数据的频数的一维数组。它表示了每个区间内数据出现的次数。
区间边界数组（bin edges）：这是一个包含直方图的区间边界值的一维数组。它表示了直方图中每个区间的边界值。
图形对象（patches）：这是一个包含绘制的直方图图形对象的列表。每个图形对象代表一个直方柱形。

我们可以利用该特性实现色彩映射，完成数据可视化。

import matplotlib.pyplot as plt
import numpy as np
import matplotlib
from matplotlib import colors


# 从 Google API 上下载暂存字体放到暂存文件夹下

!wget 'https://noto-website-2.storage.googleapis.com/pkgs/NotoSansCJKtc-hinted.zip'
!mkdir /tmp/fonts
!unzip -o NotoSansCJKtc-hinted.zip -d /tmp/fonts/
!mv /tmp/fonts/NotoSansMonoCJKtc-Regular.otf /usr/share/fonts/truetype/NotoSansMonoCJKtc-Regular.otf -f
!rm -rf /tmp/fonts
!rm NotoSansCJKtc-hinted.zip

# 指定字体
import matplotlib.font_manager as font_manager
import matplotlib.pyplot as plt
 
font_dirs = ['/usr/share/fonts/truetype/']
font_files = font_manager.findSystemFonts(fontpaths=font_dirs)
 
for font_file in font_files:
  font_manager.fontManager.addfont(font_file)
 
plt.rcParams['font.family'] = "Noto Sans Mono CJK TC"


"""
随机数生成,自动生成正态分布的数据集
"""
np.random.seed(0)
data = np.random.randn(1000)


"""
n: 数组或数组列表,表明每一个bar区间的数量或者百分比
bins : 数组,bar的范围和bins参数含义一样
patches : 列表 或者列表的列表 图形对象
"""
n, bins, patches =plt.hist(data, bins=40)
percent = n / n.max()

# 将percent中的数据进行正则化,方便映射到colormap中

norm = colors.Normalize(percent.min(), percent.max())


#在循环中，percent是一个包含数值的列表，patches是一组图形对象（例如矩形或圆形）。循环的目的是为每个图形对象设置颜色。

#首先，通过zip(percent, patches)将percent和patches两个可迭代对象进行逐个配对。这样，thisfrac将依次等于percent中的每个数值，thispatch将依次等于patches中的每个图形对象。

#接下来，norm(thisfrac)将数值thisfrac进行归一化，使其范围在0到1之间。然后，plt.cm.viridis()函数将归一化后的数值映射到颜色空间中，返回对应的颜色。

#最后，thispatch.set_facecolor(color)将图形对象thispatch的填充颜色设置为变量color所代表的颜色。

for thisfrac, thispatch in zip(percent, patches):
    color = plt.cm.viridis(norm(thisfrac)) # plt.cm.viridis()是Matplotlib中的一个内置颜色映射（colormap），用于将数值映射到颜色空间
    thispatch.set_facecolor(color)



plt.xlabel("区间")
plt.ylabel("频率")
plt.title("频率分布图")
plt.show()

双变量直方图

在基础实现中，我们实现了单变量直方图的绘制，实际中我们往往还需要进行双变量乃至多变量的相关性分析，此时使用直方图便可较为清晰地明确变量之间的关系，接下来以双变量直方图的绘制为例进行具体分析。

import matplotlib.pyplot as plt
import numpy as np
from matplotlib import colors
from matplotlib.ticker import PercentFormatter

import matplotlib.gridspec as gridspec

np.random.seed(0)
N = 1000
bins = 50

"""
生成为x,y随机数据
"""
x = np.random.randn(N)
y = x ** 2 + np.random.randn(N) + 5


fig = plt.figure(figsize=(10, 8))
# gridspec的用法，可以使图像横跨多个坐标
G = gridspec.GridSpec(2, 2) # 绘制一个2行2列的figure对象

#显示第一坐标系,其位置第一行,第一列(G[0, 0])
axes =fig.add_subplot(G[0, 0])
axes.hist(x, bins= bins)

#显示第二坐标系,其位置第一行,第二列(G[0, 1])
axes =fig.add_subplot(G[0, 1])
axes.hist(y, bins=bins)

#显示第三坐标系,其位置第二行整行(G[1, :])
axes =fig.add_subplot(G[1, :])
axes.hist2d(x,y, bins=bins)

plt.show()

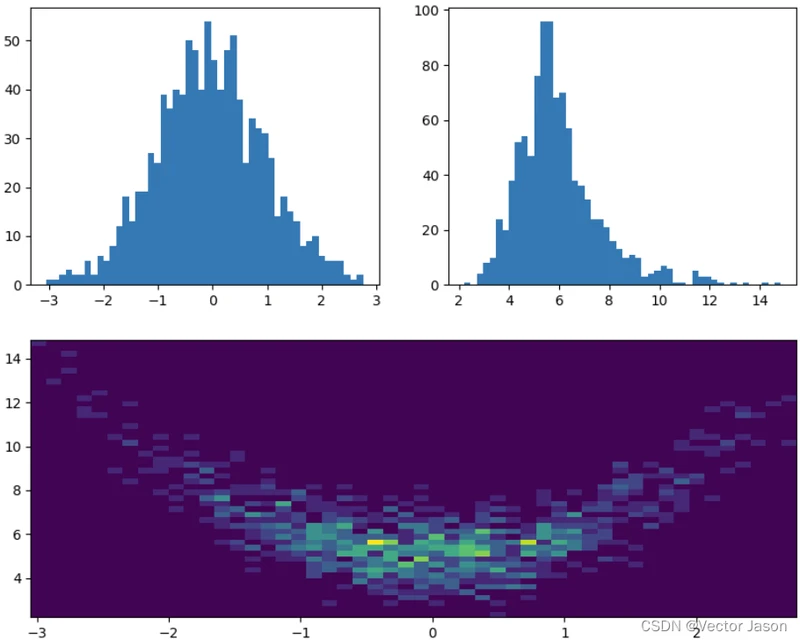
可见，此时 y 与 x^2 相关，直方图正确显示。

拟合分布曲线

绘制直方图后，我们还可以选择是否对直方图的变化趋势进行曲线拟合，这样利于判断一些难以直观发现的变化趋势。

import matplotlib.pyplot as plt
import numpy as np
import matplotlib


# 从 Google API 上下载暂存字体放到暂存文件夹下

!wget 'https://noto-website-2.storage.googleapis.com/pkgs/NotoSansCJKtc-hinted.zip'
!mkdir /tmp/fonts
!unzip -o NotoSansCJKtc-hinted.zip -d /tmp/fonts/
!mv /tmp/fonts/NotoSansMonoCJKtc-Regular.otf /usr/share/fonts/truetype/NotoSansMonoCJKtc-Regular.otf -f
!rm -rf /tmp/fonts
!rm NotoSansCJKtc-hinted.zip

# 指定字体
import matplotlib.font_manager as font_manager
import matplotlib.pyplot as plt

font_dirs = ['/usr/share/fonts/truetype/']
font_files = font_manager.findSystemFonts(fontpaths=font_dirs)

for font_file in font_files:
  font_manager.fontManager.addfont(font_file)

plt.rcParams['font.family'] = "Noto Sans Mono CJK TC"


N = 50

data = np.random.randn(1000)

fig,ax = plt.subplots()

n, bins, patches = ax.hist(data, bins = N, density=True)

# 拟合分布曲线
ax.plot(bins[:N],n,'--') # bins[:N]为横坐标， n为纵坐标


plt.xlabel("区间")
plt.ylabel("频率")
plt.title("拟合直方图")
plt.show()

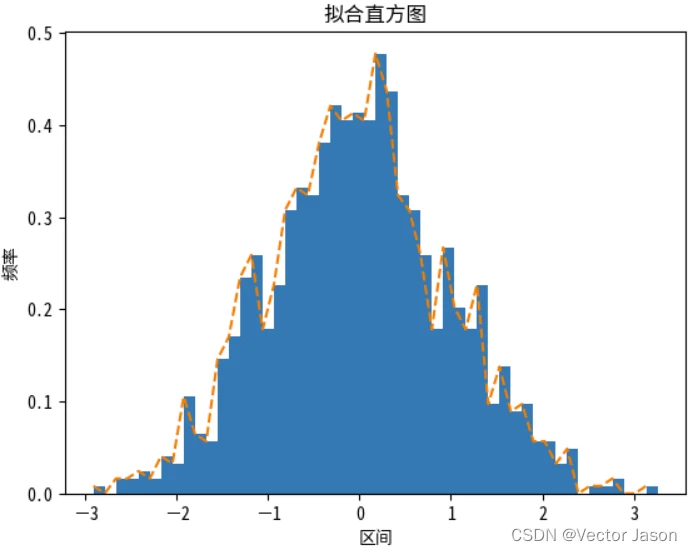
密度图

密度图是一种数据可视化技术，用于显示连续变量的分布情况。它通过在二维平面上绘制数据点的密度来展示数据的分布情况，特别适用于大量数据的可视化。

基础实现

常见的绘制密度图的方法为核密度估计（KDE），具体步骤为：KDE使用核函数对每个数据点周围的区域进行平滑，并估计该区域内数据点的密度。

import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np

# 生成一些示例数据
np.random.seed(0)
data = np.random.randn(1000)

# 创建图形对象
plt.figure(figsize=(8, 6))

# 绘制密度图
sns.kdeplot(data, fill = True)

# 设置其他绘图参数
plt.xlabel('X-axis')
plt.ylabel('Density')
plt.title('Density Plot')

# 显示密度图
plt.show()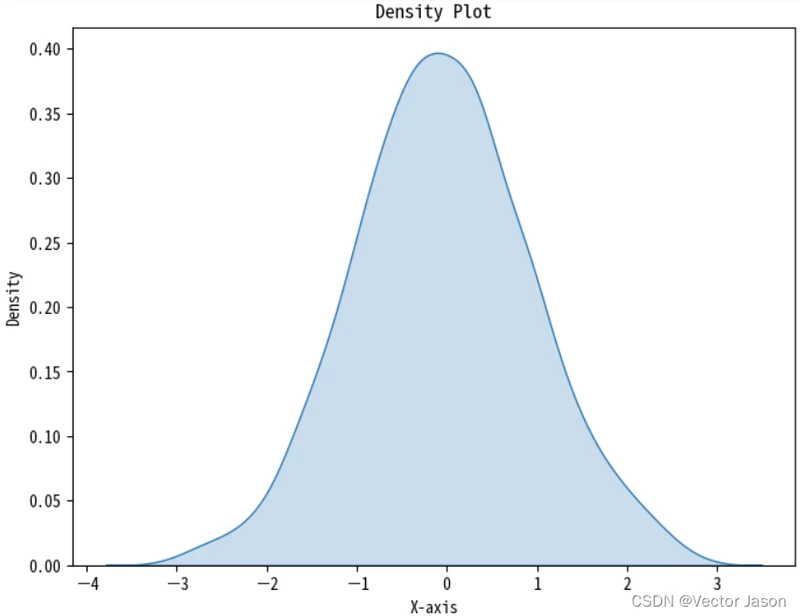

kdeplot()函数

定义：

seaborn.kdeplot(data, data2=None, shade=False, vertical=False, kernel="gau", bw="scott", gridsize=200, cut=3, clip=None, legend=True, cumulative=False, shade_lowest=True, cbar=False, cbar_ax=None, cbar_kws=None, ax=None)

参数：

data: 输入的数据，可以是一维数组、Series、DataFrame的列名或者二维数据。
data2（可选）: 用于双变量密度估计的第二个变量数据，可以是一维数组、Series、DataFrame的列名或者二维数据。
fill（可选）: 是否填充密度曲线下的区域，默认为False。
vertical（可选）: 是否将密度曲线绘制为垂直方向（默认为水平方向）。
kernel（可选）: 核函数的类型，控制密度估计的平滑程度，默认为高斯核函数（"gau"）。
bw（可选）: 带宽选择方法，用于调整密度估计的平滑程度，默认为"scott"方法。
gridsize（可选）: 网格的大小，用于计算核密度估计，默认为200。
legend（可选）: 是否显示图例，默认为True。
cumulative（可选）: 是否绘制累积密度图，默认为False。
cbar（可选）: 是否显示颜色条，默认为False。

扩展

多变量密度图

通过使用多变量核密度估计，可以绘制多变量密度图，以展示多个变量之间的联合分布情况。

import seaborn as sns

# 生成示例数据
data = sns.load_dataset("iris")

# 创建图形对象
plt.figure(figsize=(8, 6))

# 绘制多变量密度图
sns.kdeplot(data=data, x="sepal_length", y="sepal_width", hue="species", fill=True)

# 设置其他绘图参数
plt.xlabel('Sepal Length')
plt.ylabel('Sepal Width')
plt.title('Multivariate Density Plot')

# 显示密度图
plt.show()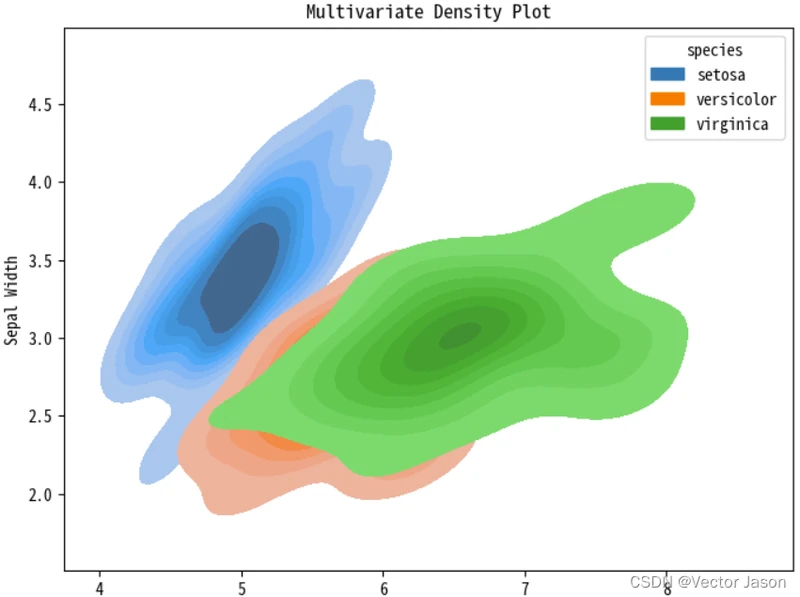

这个示例使用 seaborn 库的 kdeplot() 函数绘制了一张多变量密度图。它展示了鸢尾花数据集中萼片长度与萼片宽度之间的密度分布，并根据不同的鸢尾花种类进行了颜色编码。

分组密度图

分组密度图用于比较不同组之间的数据分布情况。通过将不同组的数据分别绘制在同一张图上，可以直观地比较它们之间的密度差异。

import seaborn as sns

# 生成示例数据
data = sns.load_dataset("tips")

# 创建图形对象
plt.figure(figsize=(8, 6))

# 绘制分组密度图
sns.kdeplot(data=data, x="total_bill", hue="time", fill=True)

# 设置其他绘图参数
plt.xlabel('Total Bill')
plt.ylabel('Density')
plt.title('Grouped Density Plot')

# 显示密度图
plt.show()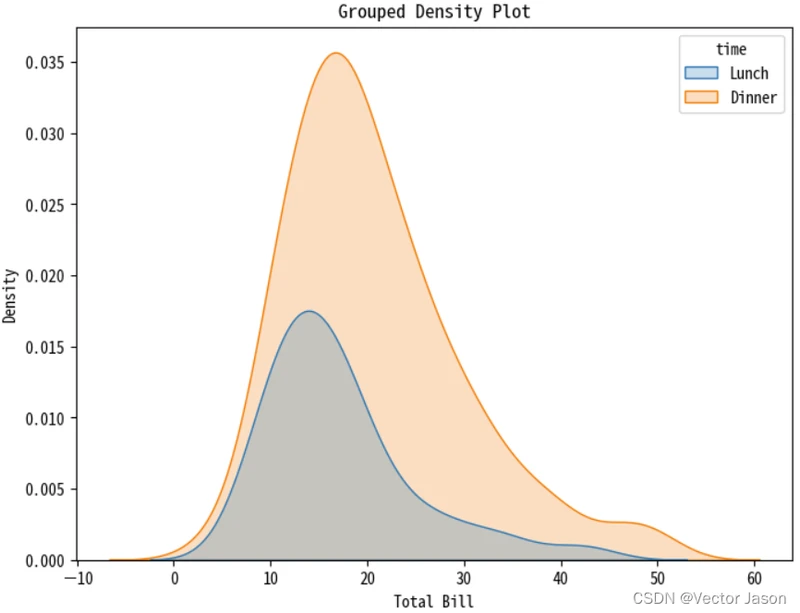

展示了不同用餐时间（午餐和晚餐）下的账单总额的密度分布，并使用颜色进行了区分。

总结

本次主要从 hist() 和 kdeplot() 两个函数具体学习了直方图与密度图的绘制，分别基于Matplotlib与Seaborn载入样例数据进行可视化，掌握了不少数据分析配图的小技巧。

直方图

基础实现

hist()函数

扩展

色彩映射

双变量直方图

拟合分布曲线

密度图

基础实现

kdeplot()函数

扩展

多变量密度图

分组密度图

总结

知秋君

相关推荐