解一元三次方程
首先要得到一个简单解这个解可以凑数得到
接着根据短除法,分解三次方程
最后每个式子等于0解得答案
具体过程:
我们观察式子
X
3
−
2
X
2
+
X
−
2
=
0
X^3-2X^2+X-2=0
X3−2X2+X−2=0,很容易找到x=2是方程的一个解,所以我们就得到一个项
X
−
2
X-2
X−2
剩下的项我们用短除法。也就是用
X
3
−
2
X
2
+
X
−
2
=
0
X^3-2X^2+X-2=0
X3−2X2+X−2=0除以
X
−
2
X-2
X−2。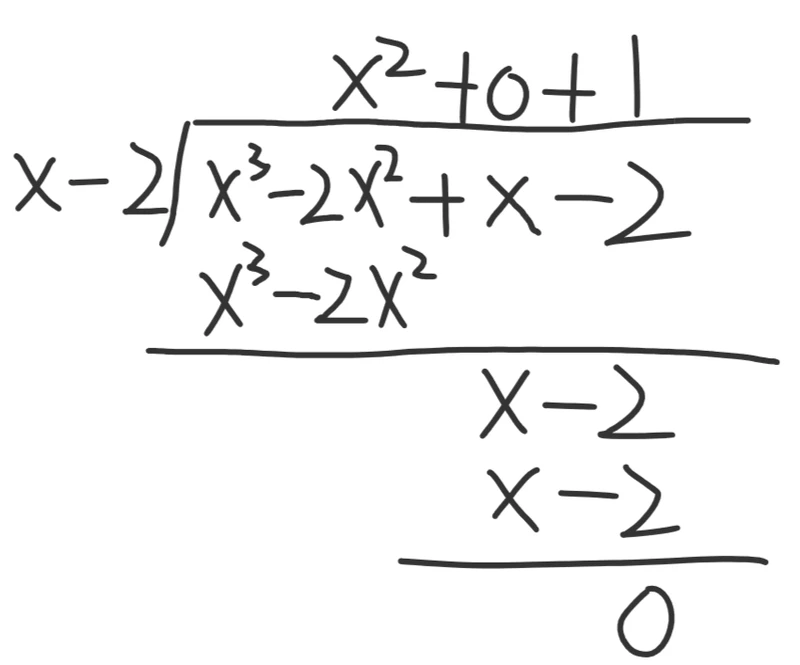
所以原式可以分解成
(
X
−
2
)
和
(
X
2
+
1
)
(X-2)和(X^2+1)
(X−2)和(X2+1)
即
(
X
−
2
)
∗
(
X
2
+
1
)
=
0
(X-2)*(X^2+1)=0
(X−2)∗(X2+1)=0
也就是解得
X
1
=
2
,
X
2
=
i
,
X
3
=
−
i
X1=2,X2=i,X3=-i
X1=2,X2=i,X3=−i
这个方法可以通用,因为大部分三次方程都是有一个简单解
觉得不错点个赞呗
转载请注明出处https://blog.csdn.net/qq_36645322/article/details/103102353
