强化学习
强化学习概念
任务:使智能体获得独立完成某种任务的能力
过程:通过环境反馈进行action,从而进入下一个状态,下一个状态会反馈给智能体一定的奖励,最终目的是达到某种策略,使得累计奖励最高
马尔科夫链

S(state)状态,是智能体观察到的当前环境的部分或者全部特征
A(action)动作,就是智能体做出的具体行为,动作空间就是该智能体能够做出的动作数量
R(reward)奖励,在某个状态下,完成动作,环境就会给我们反馈,告诉我们这个动作的效果如何,效果的数值表达就是奖励。
奖励在强化学习中,起到了很关键的作用,我们会以奖励作为引导,让智能体学习做能获得最多奖励的动作。
敲黑板:奖励的设定是主观的,也就是说我们为了智能体更好地学习工作,自己定的。所以大家可以看到,很多时候我们会对奖励进行一定的修正,这也是加速智能体学习的方法之一。
强化学习的一般步骤:
- 智能体在环境中,观察到状态(S);
- 状态(S)被输入到智能体,智能体经过计算,选择动作(A);
- 动作(A)使智能体进入另外一个状态(S),并返回奖励®给智能体。
- 智能体根据返回,调整自己的策略。 重复以上步骤,一步一步创造马尔科夫链。
马尔科夫“树”
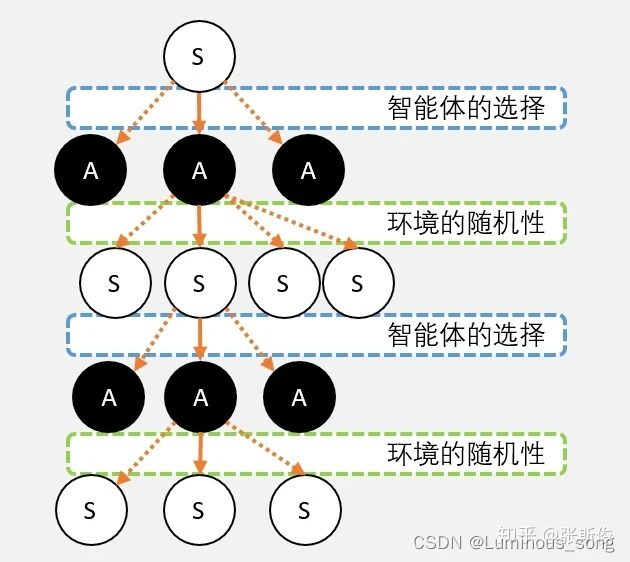
在马尔科夫链中,如果站在结果向起点看就是一条链条,但是如果站在起点看就是充满了各种“不确定性”
策略:在不同动作之间的选择,称为智能体的策略,一般用Pi表示,我们的任务就是找到一个策略,能够获得最多的奖励
不确定性:来自两个方面,一个是智能体的策略,另外一方面是环境的不确定性,例如掷骰子,智能体可以选择投几个,投掷的数量是不确定的(策略),每个骰子投出的点数也是不确定的(环境)
Q值和V值
在强化学习中会用奖励R作为智能体学习的引导,这个奖励有正有负,我们期望智能体获得尽可能多的奖励,但是很多时候不能单纯通过R来衡量一个动作的好坏。
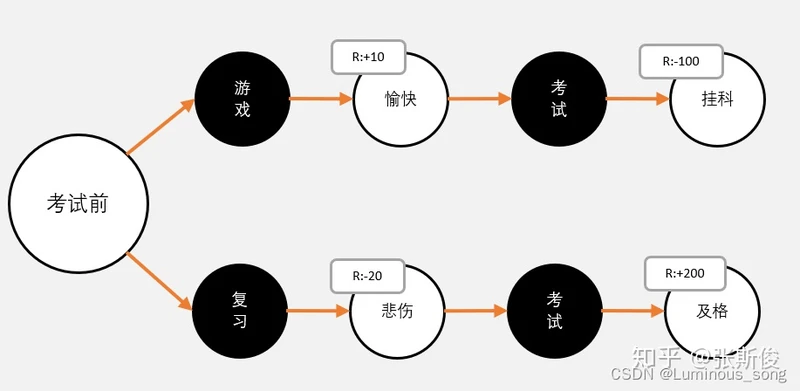
因此,我们必须用长远的眼光来看待问题。我们要把未来的奖励也计算到当前状态下,再进行决策。
复杂的未来
在实际中,会比上面图所假设的更复杂,也许我们最后考试没考好,老师也不会大发雷霆,也许复习了很久,最后也没有得到好成绩,即使得到好成绩,父母也不一定会更多的零用钱。
因此未来方便,我们对每种选择标记价值,这样每次选择的时候只要看标记,选择价值更大的就可以了
Q值:评估动作的价值,代表智能体选择这个动作后,一直到最终状态奖励总和的期望
V值:评估状态的价值,代表智能体在这个状态下,一直到最终状态的奖励总和的期望。
V值
求某状态S的V值,步骤:
- 从S点出发,影分身出若干个自己
- 每个分身按照当前的策略选择行为
- 每个分身一直走到最终状态,并计算一路上获得的所有奖励总和
- 计算每个影分身获得的平均值( ∑ r e w a r d 分身数量 \frac{\sum{reward}}{分身数量} 分身数量∑reward),这个平均值就是V值
从某个状态,按照策略 ,走到最终状态很多很多次;最终获得奖励总和的平均值,就是V值。
V值会根据不同的策略有所变化,如果采用平均策略(50% 50%)V值为15,如果改变策略(60% 40%)V值为14
Q值
Q值和V值相似,但是Q值衡量的是动作结点的价值
用大白话总结就是:从某个状态选取动作A,走到最终状态很多很多次;最终获得奖励总和的平均值,就是Q值。
【敲黑板】 与V值不同,Q值和策略并没有直接相关,而与环境的状态转移概率相关,而环境的状态转移概率是不变的。
Q值与V值相互计算
Q->V
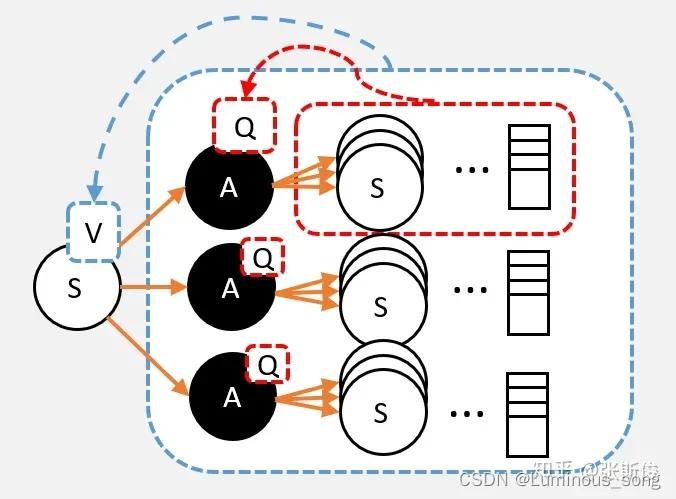
我们要求V值,也就是从状态S出发,到最终状态获取的奖励总和的期望值,S状态下有很多个动作,这些动作的Q值,即这个动作之后到最终状态获得奖励总和的期望,那么在计算V值的时候就不需要走到最终状态了,只需要到action,看动作的Q值,计算Q值的期望就是V值
v
π
(
s
)
=
∑
a
∈
A
π
(
a
∣
s
)
q
π
(
s
,
a
)
v_{\pi}(s) = \sum_{a\in{A}}\pi(a|s)q_{\pi}(s,a)
vπ(s)=∑a∈Aπ(a∣s)qπ(s,a)
V->Q
还是一样的道理,计算Q值就是V值的期望,而且这里不需要关注策略,这里是环境的状态转移概率决定。但是选择A的时候会转移到新的状态,就可以获得奖励,需要把这个奖励也算上
q
π
(
s
,
a
)
=
R
s
a
+
γ
∑
s
′
P
s
s
′
a
v
π
(
s
′
)
q_{\pi}(s,a) = R^{a}_{s} + \gamma\sum_{s'}P^{a}_{ss'}v_{\pi}(s')
qπ(s,a)=Rsa+γ∑s′Pss′avπ(s′)
其中
R
s
a
R^{a}_{s}
Rsa是奖励
γ
\gamma
γ是折扣率,在强化学习中某些参数是人为主观设定的,这些参数不能被推导,但是在现实生活中却能解决问题,把这些参数称为超参数,折扣率就是一个超参数,也就是未来n步的10点与现在的10点奖励未必等价,因此人为的给未来的奖励设定一定的折扣,然后计算当前的Q值
P
s
s
′
a
P^{a}_{ss'}
Pss′a是状态转移概率
V->V
把Q->V公式代入V->Q即可
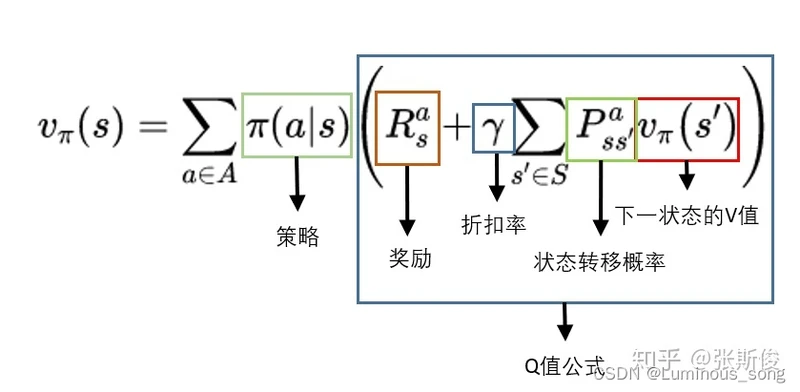
计算V值
在前面Q值和V值都需要许多次实验,来取平均值,这样的消耗会很大,因此人们发明了许多方式计算Q值和V值。
蒙地卡罗算法(MC)
蒙地卡罗算法:
- 我们把智能体放到环境的任意状态;
- 从这个状态开始按照策略进行选择动作,并进入新的状态。
- 重复步骤2,直到最终状态;
- 我们从最终状态开始向前回溯:计算每个状态的G值。
- 重复1-4多次,然后平均每个状态的G值,这就是我们需要求的V值。
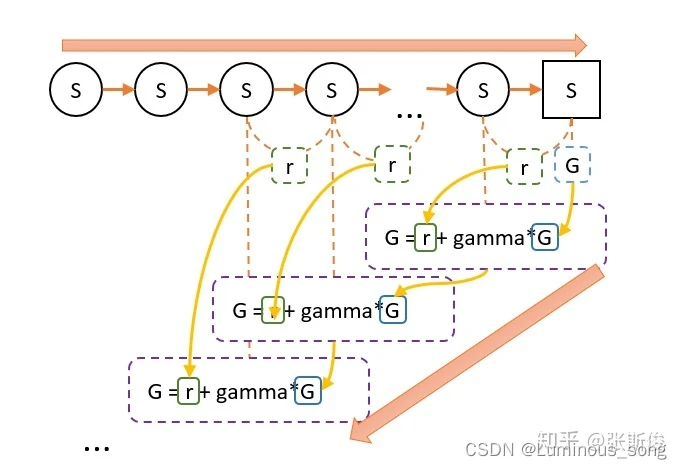
G值的意义在于,在这一次游戏中,某个状态到最终状态的奖励总和(理解时可以忽略折扣值)
V和G的关系:V是G的平均数。
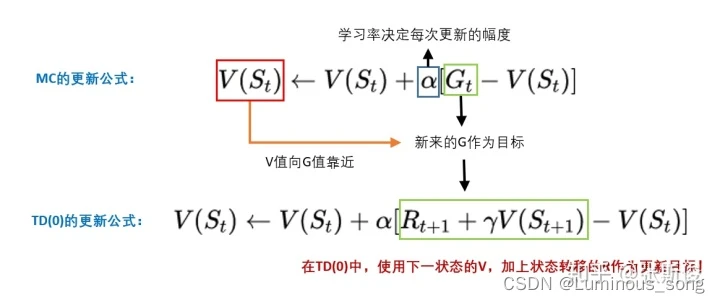
V的更新公式,
V
n
e
w
=
(
G
−
V
o
l
d
)
∗
(
1
/
N
)
+
V
o
l
d
V_{new} = (G - V_{old}) * (1 / N) + V_{old}
Vnew=(G−Vold)∗(1/N)+Vold
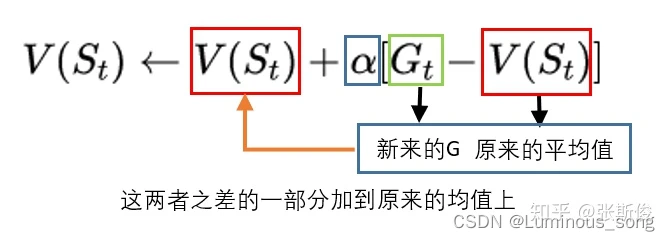
但蒙地卡罗有一个比较大的缺点,就是每一次游戏,都需要先从头走到尾,再进行回溯更新。如果最终状态很难达到,那小猴子可能每一次都要转很久很久才能更新一次G值。
时序差分算法(TD算法)
算法:
- 小猴子每走1步,看一下这个路口的V值还有获得的奖励r
- 回到原来的路口,把刚刚看到的V值和奖励值进行运算,估算出V值
状态的V值怎么算呢?其实和蒙地卡罗一样,我们就假设N步之后,就到达了最终状态了。
- 假设“最终状态”上我们之前没有走过,所以这个状态上的纸是空白的。这个时候我们就当这个状态为0.
- 假设“最终状态”上我们已经走过了,这个状态的V值,就是当前值。然后我们开始回溯。
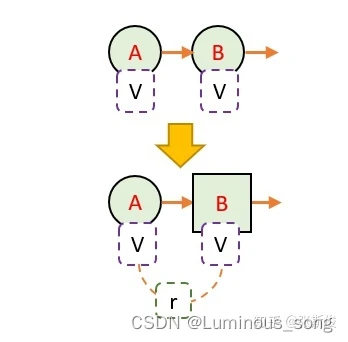
我们从A状态走一步到B状态,我们就把B状态当做最终状态,而B状态本身带有一定的价值,也就是V值,如果B状态的V值是对的,那么,通过回溯计算,我们就能知道A状态的更新目标了。