过拟合和欠拟合
过拟合是指训练误差和测试误差之间的差距太大。就是模型复杂度高于实际问题,模型在训练集上表现很好,但在测试集上却表现很差。
措施:
1、增加数据集
2、加入正则化
3、进行特征选择
4、提前停止训练,深度学习中常用dropout策略。
欠拟合是指模型不能在训练集上获得足够低的误差。换句换说,就是模型复杂度低,模型在训练集上就表现很差,没法学习到数据背后的规律。
措施:
1、增加模型复杂度和训练次数
2、增加新特征,增大假设空间
3、如果有正则项,可以调小正则项参数
偏差方差理论
偏差、方差、噪声
偏差:度量了模型的期望预测和真实结果的偏离程度,刻画了模型本身的拟合能力。
方差:度量了同样大小的训练集的变动所导致的学习性能的变化,即刻画了数据扰动所造成的影响。
噪声:表达了当前任务上任何模型所能达到的期望泛化误差的下界,刻画了学习问题本身的难度。
偏方差分解

在实际的问题中噪音是数据自带的,没有办法优化,因此为了优化模型,降低模型的泛化误差,我们便从降低偏差和方差入手,但是方差和偏差存在权衡问题,即在优化一个时便会导致另一个升高,下面给出了泛化误差和偏差、方差的变化关系,
在训练不足时,模型的拟合能力不强,此时偏差主导着总体误差(泛化误差),随着训练程度的加深,模型的拟合能力已经很强,训练数据发生的噪音扰动也被模型学到,方差逐渐主导总体误差。
正则化

以上是以线性回归为例。lamda越小意味着复杂度越大
正则化是为了防止过拟合, 进而增强泛化能力
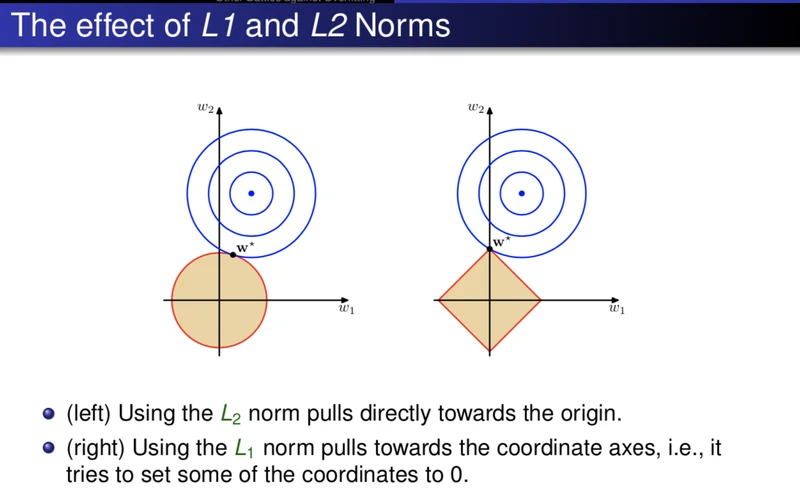
L1和L2正则化的目的都是减少模型的复杂度。
L1正则化可以产生稀疏权值矩阵,即产生一个稀疏模型,可以用于特征选择
L2正则化可以防止模型过拟合(overfitting);一定程度上,L1也可以防止过拟合
当对损失进行求导时,对参数b进行求导,可发现正则化对其没有影响,而当对参数w进行求导时,可以发现正则化对w的影响。


