传统的公钥密码PKE
( G e n , E n c , D e c ) (Gen,Enc,Dec) (Gen,Enc,Dec)
其中 G e n Gen Gen生成的密钥对为 ( p k , s k ) (pk,sk) (pk,sk)
发送方用公钥进行加密 C ← E n c p k ( m ) C\leftarrow Enc_{pk}(m) C←Encpk(m)
接收方用自己的私钥进行解密 m : = D e c s k ( c ) m:=Dec_{sk}(c) m:=Decsk(c)
公钥密码的缺点:计算速度慢,效率比对称算法低太多了公钥密码效率低的原因?

首先这里讨论有关效率的指标有这些:CPU、network bandwidth也就是网络带宽、functionalites功能性
“moral”的原因是因为,首先,如何做到pk不泄露sk的信息,这已经是需要很强数学能力的事情了(attacker不能通过公钥去破解出私钥)
相比对称密码只是简单的打乱比特来说,公钥密码的方法更复杂的多
而且,一些已知的非对称加密系统看起来实现了我们需要的安全,但实际上需要巨大的计算开销。注意到McEliece cryptosystem 和 NTRUEncrypt都实现了高速下的非对称加解密方案(比RSA,椭圆曲线下的El Gamal快多了)。
并没有证据表明非对称加密在计算方面比对称加密更难。
带宽是非对称加密算法中另一个效率指标。这绝对是限制加密算法效率的因素之一。公钥密码算法是公开的,意味着任何人包括攻击者都能使用公钥去加密任意的消息。这意味着如果加密算法是确定的,那么攻击者就可以通过穷举得到匹配的密文。因此一个非对称加密算法还需要包含额外的随机性。
这样的额外的随机性就使得加密数据的大小增加。
例如,RSA使用1024位密钥,最多只能加密117字节的数据元素,从而产生128字节的密文。因此,如果你只用RSA加密一个大文件,那么最终加密的明文会比密文多出%9的信息。对于10GB的消息来说,这就是900M的冗余信息。除此之外,对称加密只会产生固定的开销。在大多数场景下,网络带宽都是比CPU要更稀缺的资源
因此出现了密钥协商的方案。这跟公钥密码非常像。
回归正题
crystal kyber其实就是这样一个用非对称加密的思想去封装密钥并进行密钥协商的算法。主要聚焦的也是在KEM(key encapsulation mechanism)
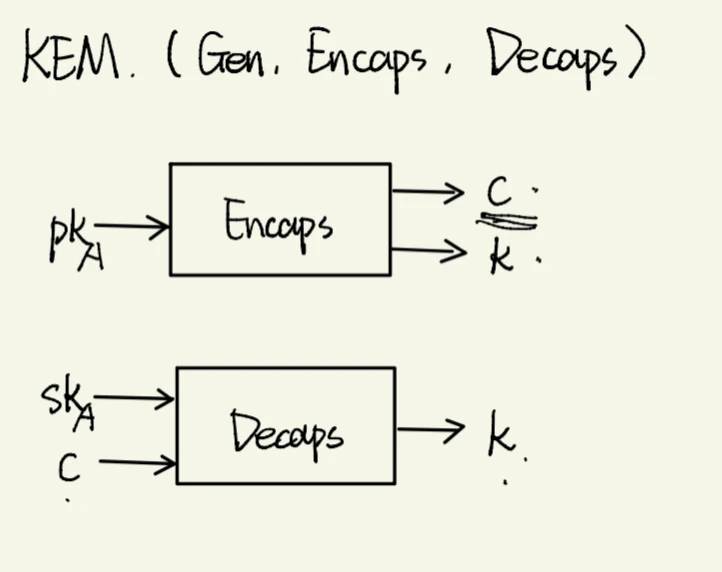
如何生成pk和sk,并且pk不会暴露sk的信息?
这里就用到了LWE(learning with errors)问题。LWE是格上的一类困难问题。Crystal kyber算法用到了环上的LWE问题(Ring-LWE)。
什么是LWE问题?
- 已知一种情况: s ∈ Z q n \boldsymbol{s} \in \mathbb{Z}_{q}^{n} s∈Zqn(其中 Z q n \mathbb{Z}_{q}^{n} Zqn相当于一个n维向量,每一维都是 Z m o d q \mathbb{Z} mod q Zmodq,也就是 { 0 , 1 , 2 , . . . , q − 1 } \left\{0,1,2,...,q-1\right\} {0,1,2,...,q−1}), a ∈ Z q n \boldsymbol{a} \in \mathbb{Z}_{q}^{n} a∈Zqn, b ∈ Z q b \in \mathbb{Z}_{q} b∈Zq,则 ( a , b ) ∈ Z q n × (\boldsymbol{a}, b) \in \mathbb{Z}_{q}^{n} \times (a,b)∈Zqn× Z q \mathbb{Z}_{q} Zq。那么我们可以想象一个黑盒,黑盒内部的运算规则为,输入 a \boldsymbol{a} a,经过 < s , a > <\boldsymbol{s},\boldsymbol{a}> <s,a>的点乘运算后,得到 b b b。在外界看来,不知道 b b b是怎么获得的,只知道 a \boldsymbol{a} a和 b b b,在这种情况下,求出 s \boldsymbol{s} s是容易的。
- 另一种情况:黑盒中的点乘运算加入了误差项 e {e} e,也就是 b = < s , a > + e b=<\boldsymbol{s},\boldsymbol{a}>+e b=<s,a>+e,这个 e {e} e可以是任意的噪声,这个时候,外部再要通过 a \boldsymbol{a} a和 b b b求出 s \boldsymbol{s} s就非常困难了。
环LWE还没讲所以先空在这下次补充
上面我们知道了环LWE问题求解
s
{s}
s是困难的,因此可以利用这个困难问题去生成
(
p
k
,
s
k
)
(pk,sk)
(pk,sk)密钥对。
主要流程如下。


下面我们依次解读其中用到的算法。
B
32
\mathcal{B}^{32}
B32表示长度为32的8位无符号整数字节矩阵,通过调用randombytes函数得到。
https://github.com/dsprenkels/randombytes
-
G G G函数用SHA3-512实例化

-
P a r s e Parse Parse函数
Input:字节流B
Output:多项式环
i:=0
j:=0
while j<n do
d1:=bi+256*(bi+1 mod+ 16)
d2:=round(bi+1/16)+16*bi+2
if d1<q then
ajhead:=d1
j:j+1
end if
if d2<q and j<n then
ajhead:=d2
j:=j+1
end if
i:=i+3
end while
return a0head+a1headX+...+an-1headXn-1

注:这里有个疑问,怎么实现
m
o
d
+
\bmod ^{+}
mod+ ?
P
a
r
s
e
Parse
Parse函数的输入是
X
O
F
(
ρ
,
j
,
i
)
\mathrm{XOF}(\rho, j, i)
XOF(ρ,j,i),
X
O
F
\mathrm{XOF}
XOF刚刚有提到是SHAKE-128
- C B D CBD CBD函数(“center binomial distribution”)
