题目来源
- leetcode:689. 三个无重叠子数组的最大和
题目描述

class Solution {
public:
vector<int> maxSumOfThreeSubarrays(vector<int>& nums, int k) {
}
};
题目解析
分析数据
- 1 < = n u m s . l e n g t h < = 2 ∗ 1 0 4 1 <= nums.length <= 2 * 10^4 1<=nums.length<=2∗104:时间复杂度最多O(N*logN)
- 1 < = n u m s [ i ] < 2 16 1 <= nums[i] < 2^{16} 1<=nums[i]<216:数组中元素一定是正数,而且数据范围很大
- 1 < = k < = f l o o r ( n u m s . l e n g t h / 3 ) 1 <= k <= floor(nums.length / 3) 1<=k<=floor(nums.length/3):floor表示向下取整,因此保证了数组长度至少为3
分析题意
从一个数组中选出3段,其特征:
- 互不重叠,每一段的长度都是K
- 三段之和加起来最大
分析
- 因为要选出3端
- 当k = 1时,如果要选出互不重叠而且每一段长度都是1的3端,那么数组长度必须>=3
- 当k = 2时,如果要选出互不重叠而且每一段长度都是2的3端,那么数组长度必须>=6
- 当k = 3时,如果要选出互不重叠而且每一段长度都是3的3端,那么数组长度必须>=9
- 因此,在算法的最先开始时,可以做一个大过滤器
思路
-
题目要求我们从一个数组中选出3个子数组,并且它们的和最大,应该怎么选择呢?
-
我们降维分析:如果要从一个数组中选出3个数,并且它们的和最大,应该怎么选择呢?
-
我们再降一维分析:如果要从一个数组中选出2个数,并且它们的和最大,应该怎么选择呢?
- 我们可以枚举必须以 n u m s [ i ] nums[i] nums[i]为结尾时,然后从 n u m s [ 0...... i − 1 ] nums[0......i-1] nums[0......i−1]中选出一个最大的,和当前数组合,然后得到值 s u m i sum_i sumi
- 然后从所有值 s u m [ 0... N − 1 ] sum[0...N-1] sum[0...N−1]中选出一个最大的,那就是答案
-
回到上一维:如果要从一个数组中选出3个数,并且它们的和最大,应该怎么选择呢?
- 我们可以枚举必须选择 n u m s [ i ] nums[i] nums[i]时,从 n u m s [ 0...... i − 1 ] nums[0......i-1] nums[0......i−1]中选出一个最大的,然后从 n u m s [ i . . . . . . N − 1 ] nums[i......N-1] nums[i......N−1]中选出一个最大的,它们三个组合,然后得到值 s u m i sum_i sumi
- 然后从所有值 s u m [ 0... N − 1 ] sum[0...N-1] sum[0...N−1]中选出一个最大的,那就是答案
-
回到上一维:我们从一个数组中选出3个子数组,并且它们的和最大,应该怎么选择呢?
- 从索引k开始枚举:我们可以固定住中间的那个长度为k的子数组,从两边开始找
- 只能选取[0…k-1]作为前一段,固定住[k…k + k - 1]作为第二段,从[k+k…N-1]找出最大的第一段(长度为K,sum最大)作为第三段。记下和
- 从[0…k]找出最大的第一段(长度为K,sum最大),固定住[k+1…k + k - 1 + 1]作为第二段,从[k+k+1…N-1]找出最大的第一段(长度为K,sum最大)作为第三段。记下和
- 当start = ((N-1)-2k)+1就可以停止枚举了
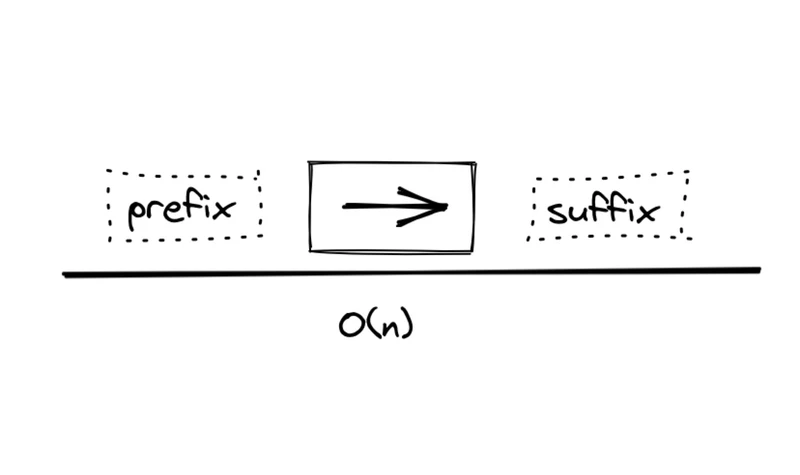
- 从索引k开始枚举:我们可以固定住中间的那个长度为k的子数组,从两边开始找
那么问题就转换为:
- 在nums[0…i]位置上,选出一个长度为k的子数组(不能不选),它们的和最大
- 在nums[i…N-1]位置上,选出一个长度为k的子数组(不能不选),它们的和最大
也就是说,我们需要同时:找到左侧的最大值,同时找到右侧的最大值
跟接雨水那道题类似,但是这里不能单纯的从左边右边移动一位,而是对应的需要移动距离k之外的最大值
动态规划
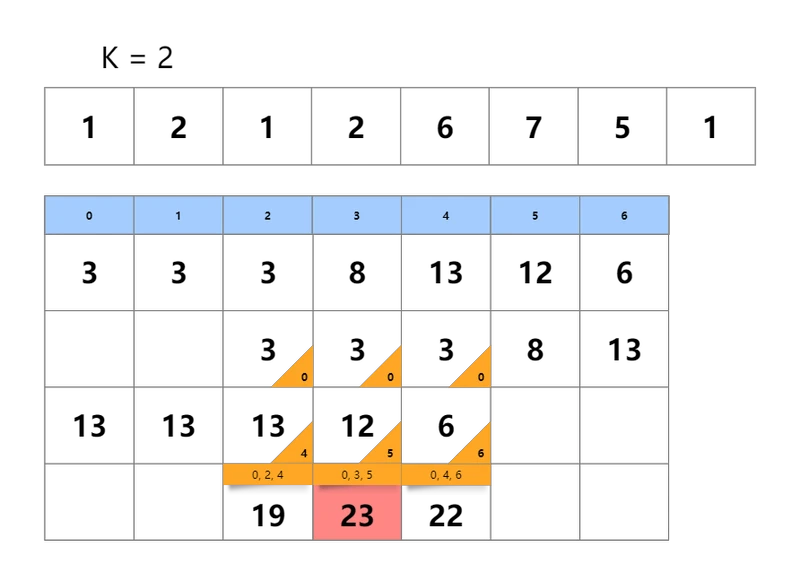
- 首先求得sumK数组 3 3 3 8 13 12 6
- 接下来分别求左侧和右侧的最大值,下标0,1没有左侧区间,下标5,6也没有右侧区间
- 左侧最大值从下标2开始,对应值为sumK[0],之后往右移动,下标5的左侧最大值为sumK[3],下标6同理
- 最终只遍历中间部分左右侧最大值都有的区间,找到和最大的那个值,并记下对应的下标索引
class Solution {
public:
vector<int> maxSumOfThreeSubarrays(vector<int>& nums, int k) {
int N = nums.size();
std::vector<int> sumK(N - k + 1);
for (int i = 0; i < k; ++i) {
sumK[0] += nums[i];
}
for (int i = 0; i < sumK.size(); ++i) {
sumK[i] = sumK[i - 1] + nums[i + k - 1] - nums[i - 1];
}
std::vector<std::vector<int>> dp(sumK.size(), std::vector<int>(2));
bool flag =false;
for (int i = k; i < sumK.size() - k; ++i) {
int j = sumK.size() - i - 1;
if (flag){
dp[i][0] = sumK[i-k] > sumK[dp[i-1][0]] ? i-k : dp[i-1][0];
dp[j][1] = sumK[j+k] >= sumK[dp[j+1][1]] ? j+k : dp[j+1][1];
}else{
flag = true;
dp[i][0] = i-k;
dp[j][1] = j+k;
}
}
vector<int> res(3, 0);
int max = 0;
// 枚举第二个数,边界需考虑清楚
for (int i = k; i + k < sumK.size(); ++i) {
int sum = sumK[i] + sumK[dp[i][0]] + sumK[dp[i][1]];
if ( sum > max){
max = sum;
res[0] = dp[i][0];
res[1] = i;
res[2] = dp[i][1];
}
}
return res;
}
};
