感谢大神分享:https://zhuanlan.zhihu.com/p/131342530
1. 概述
标定的本质是参数辨识。首先明确哪些参数可辨识,其次弄清怎样辨识。
参数包括陀螺仪和加速度计各自的零偏、标度因数、安装误差。
辨识就比较丰富了,如果让各位先不局限于标定任务,想一想你了解的辨识方法有哪些,常见的回答应该有这样几个:
1)解析法或最小二乘
2)滤波(kalman等)
3)梯度下降迭代优化
确实没错,标定里用的就是这些方法。这说明标定其实就是一个普通的参数辨识问题,它和你遇到的其他参数辨识任务比,并没有特殊在哪里。
本篇文章我们先分析标定的 误差参数、误差模型,然后介绍第一种参数辨识方法。这种方法要知道真实的加速度和角速度输入,
一般要有转台才能具备这个条件,所以可以把它归类为基于转台的标定。其他的标定方法,我们下一篇文章再讨论。
2. 标定参数分析
1) 零偏
这个比较好理解,就是输出比输入多了一个常值误差。
需要注意的是,我们之前通过Allan方差分析,得到了器件的 量化噪声、角度随机游走、角速率随机游走、零偏不稳定性噪声、速率斜坡,
仔细看,这些都是对零偏质量的分析,也可以直观的理解为零偏的波动和漂移程度,这里面并没有分析零偏本身的大小,而这个才是我们标定里要去估计的那个常值误差。
加速度计的零偏在这里表示为
![]()
陀螺仪的零偏在这里表示为

2) 标度因数误差
假设器件输出的是标准单位角速度,那么输出和输入的比就是1。如果不是,就得需要标定,并修正这个比例。
可恶的是,这个误差不一定是常值,它会随着输入大小的不同而发生变化,这个就是标度因数的非线性。如果非线性程度比较大,
则需要在标定之前先拟合该非线性曲线,并补偿成线性再去做标定。加速度计的标度因数这里表示如下:

陀螺仪的标度因数这里表示为:

3) 安装误差
一图胜千言,上图吧 !
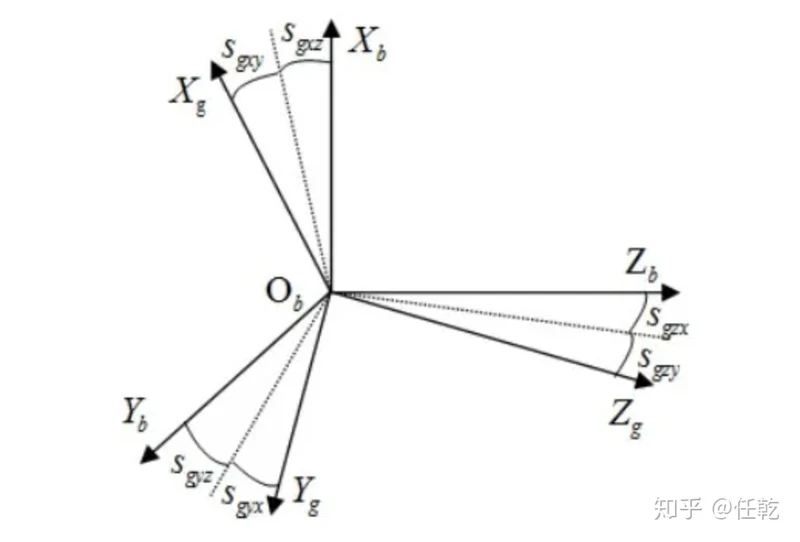
这里面b坐标系是正交的imu坐标系,g坐标系的三个轴是分别对应三个陀螺仪。由于加工工艺原因,陀螺仪的三个轴并不正交,
和我们导航中使用的正交轴不重合。我们需要仔细想一想,这个安装误差怎么在陀螺输出中体现出来的,因为我们标定时只能
采集到陀螺的输出,而无法直接去测量安装误差。理论上,在陀螺坐标轴和b系重合的情况下,我们沿b系某一个坐标轴旋转,
那么其他两个轴是不会有角速度输出的,而有了安装误差以后,便有了输出,据此,我们就可以建立输出和误差之间的关系了。
以图中一项误差为例,Sgxy表示的就是y轴的单位输入,在x陀螺上由安装误差造成的输出。由此,我们可以把所有的安装误差都成矩阵形式,即:
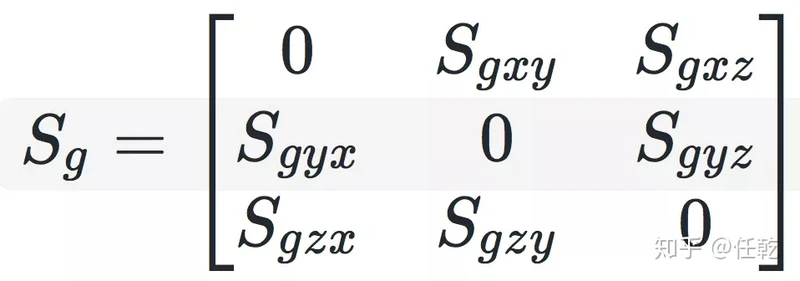
加速度计的安装误差原理和它一样,直接给出公式。

这样一共有12项安装误差参数。有的时候,可以简化为9项,但在其他标定方法中使用比较多,本次的方法不使用,所以等后面用到时再详细分析。
3. 误差模型
通过上面的参数分析,我们已经可以很容易地写出误差模型了。
陀螺仪:
![]()
其中W是陀螺输出,ω是各坐标轴真实输入。
加速度计:
![]()
其中A是加速度计输出,a是三个轴真实输入。
展开来看,就是这样的:
陀螺仪:

加速度计:
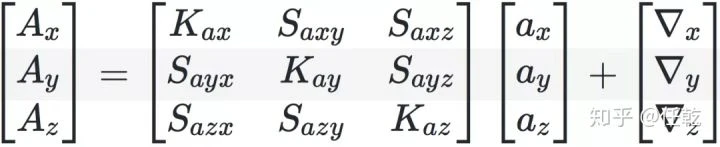
4. 基于转台的标定
1) 标定原理
在说标定之前,我们先看几个简单的小问题。
第一个问题,假如给你下面的方程组,你会怎么解

应该都能想到,用2式减去1式,得到y=1,然后带入1式,得到x=0。
第二个问题,下面的式子里,你可以随意给定a和b的值,并同时会得到c的结果,这个x和y怎么解。
![]()
也很简单,首先a=1,b=0,得到x,然后把a=0,b=1得到y。
第三个问题,下面式子,同样是输入a和b,得到c1和c2,怎么解。

其实就是前两个问题的结合,先让a=0,转成问题1,得到x和y,随后让a=1,得到z。
第四个问题,给你下面的式子,可以随意更改ax、ay和az,怎么解。

想必凭各位的冰雪聪明,一定知道我在说什么了。到这里,虽然还没讲标定,但你已经懂标定了;标定就是通过改变输入,来构建方程组,去解这个方程。
2) 标定方法
转台等同于真实输入,当把IMU安装在转台上时,IMU坐标系每个轴上的真实角速度和加速度都是已知的(这里是在转台经过调平和对准的情况下)。
你转动转台的过程,就是构建方程去求解参数的过程。举个例子,当把IMU竖直向上放的时候,有
![]()
我们可以得到:
![]()
竖直向下放的时候,可以得到:
![]()
这样就很容易解出Kaz和加速度计零位了。
经过多次这样的操作,就可以求解所有参数,这就是我们看到的标定资料里全是多位置转位方案的原因。另外,可以看出,
我们每次只给一个轴输入,另外两个轴为零,这样做的好处是每一次得到的方程就只包含一小部分参数,使求解变得简单。
这也就是为什么我们看到的多位置标定方案都是以90度为单位进行旋转的原因。
另外,需要注意的是,由于器件有噪声,所以输出值都是用一段时间的数据取平均,而不是只选择一个时间点的值。
5. 拓展思考
1) 最小二乘的使用
理论上,能够解析求解的,都能够用最小二乘求解。都学过线性代数,把系数矩阵提取出来,构建多组输入输出,就可以计算了,
前提是系数矩阵要满秩。各位如果感兴趣,可以根据标定误差模型,自己写一下误差参数的系数矩阵。
我们能够想到一点,既然在最小二乘的方法里,不需要自己去解析求解方程了,那么其实就没必要只给一个轴输入了,而现实中为什么不这样做呢?
因为它没有带来额外的好处,对于改变了虽然也能实现,但没有额外好处的做法,工程中一般不会主动去做,所以还是沿用原来的了。
此处留一个小小的问题,供大家思考:由于最小二乘要一次性求解参数,即系数矩阵要满秩,那么我们应该怎样多次旋转和停放转台才能够使它满秩呢?
进一步,旋转和停放的次数最少是多少呢?
2) 包含未知输入
我们在介绍标定方法的时候,是在假设转台经过调平和对准的前提下。所谓转台调平,就是转台安装面和地面平行,这样地球重力加速度在IMU各
个轴上的输入才是已知的,否则,如果转台和水平面有个夹角,且夹角未知,那么仪表的真实输入就不可计算了。所谓转台对准,是指转台的方向
和地理系北向是对齐的,这样地球自转角速度在陀螺仪上的分量就是已知的,反之则未知。
这个问题是能够解决的,但是我们先不直接给出方法,而是同样用解方程的方式来表达这种思路。我们看下面的方程,可以输入任意a和b,得到c,里面x、y、m、n都是未知的。
![]()
可以看出,我们能够计算出x和y,而不能分别算出m和n。但是换一个角度,如果我们只需要x和y呢,也就是说,
在一个不完全可解的方程里,如果我们想要的恰恰是那些可解的参数,也足够了。
回到标定的问题,如果转台没有调平和对准,引入了未知数,那么是否也一样能识别出要标定的参数呢?
这时候最小二乘方法是否仍然可以使用?这作为本篇文章的第二个问题,供大家思考。
五、IMU误差标定之系统级标定
