先做一个声明:文章是由我的个人公众号中的推送直接复制粘贴而来,因此对智能优化算法感兴趣的朋友,可关注我的个人公众号:启发式算法讨论。我会不定期在公众号里分享不同的智能优化算法,经典的,或者是近几年提出的新型智能优化算法,并附MATLAB代码。
“星鸦优化算法是一个2023年刚提出的新算法,发表在国际顶级刊物KBS上,大家可以选择作为对比算法~
关于这个中文名翻译,有的人翻译成星雀或星鸟,更有甚者翻译为胡桃夹子。我查阅了一下这种鸟类,按照英文名对照过来的话,我觉得应该翻译成星鸦~
这个算法非常新,性能也很不错,可以学习一下~”




星鸦优化算法(Nutcracker Optimization Algorithm, NOA)是一种新颖的自然启发的元启发式算法,灵感来自克拉克的星鸦。星鸦在不同的时期表现出两种不同的行为。第一种发生在夏季和秋季,星鸦寻找种子并随后将其储存在适当的贮藏处。第二种发生在冬季和春季,星鸦基于空间记忆利用各种物体或标记作为参考点,寻找不同角度标记的隐藏贮藏物。如果星鸦找不到储存的种子,它们会随机地探索搜索空间来寻找食物。作者通过23个经典Benchmark函数、CEC2014测试集、CEC2017测试集和CEC2020测试集以及5个工程问题对NOA进行评估。与现有的三类优化算法进行了比较:(1)近两年发表的SMA、GBO、EO、RUN、AVOA、RFO和GTO算法;(2)SSA、WOA和GWO等高引用算法;(3)AL-SHADE、L-SHADE、LSHADE-cnEpSin和LSHADE-SPACMA等CEC优胜者算法。实验结果表明NOA在所有方法中排名第一,综合性能最优。它的原始参考文献如下:
“Abdel-Basset M, Mohamed R, Jameel M, et al. Nutcracker optimizer: A novel nature-inspired metaheuristic algorithm for global optimization and engineering design problems[J]. Knowledge-Based Systems, 2023, 262: 110248.”

01
灵感来源
克拉克的星鸦是生活在美国西部和加拿大山区的高纬度居住的鸦科物种。克拉克的星鸦是一种浅灰色的鸟,有着黑色的翅膀。这些鸟经常独自生活,不像乌鸦等鸦科的其他物种那样生活在家庭群体中。松子是克拉克星鸦的主要食物来源。

星鸦在冬天依靠储存的种子生存。贮藏行为一直持续到种子作物枯竭或恶劣天气的介入。此外,星鸦从树上收集种子的效率很高,可以选择高于平均水平的好种子。星鸦收集松子,储藏在树洞里和树根底下,准备冬天吃。每只星鸦找到的储藏食物不一定是自己储藏的,自己储藏的松子也可能成为别人的食物。
NOA主要基于星鸦的搜索、贮藏和找回行为。
02
算法设计
如前所述,星鸦的行为可以分为两个主要部分:第一部分是收集松树种子(食物)并储存它们;第二部分是搜索和检索存储地点。这两种行为的特点是发生在两个不同的时期:第一种行为发生在夏天和秋天;第二种行为发生在冬季和春季。在提出的NOA中,作者基于上述两个主要行为来模拟星鸦的行为。两种主要策略是:(1)觅食和储存策略(Foraging and storage strategy);(2)缓存搜索和找回策略(Cache-search and recovery strategy)。而在两种策略中,星鸦种群均存在勘探(Exploration)和开发(Exploitation)的过程,即每种策略又包含了两种不同的种群行为,如图1所示。
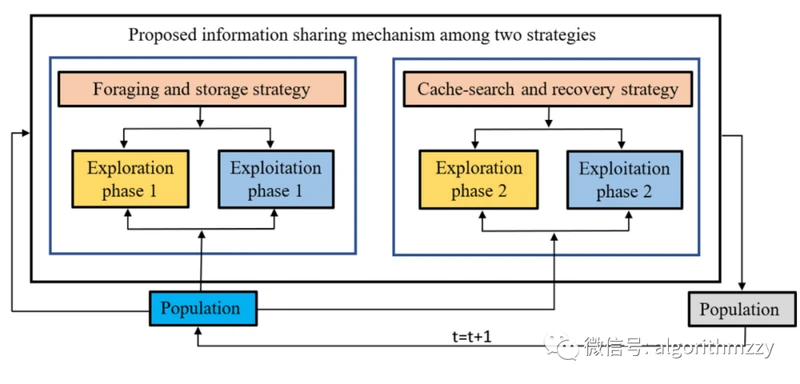
图1 NOA的基本框架
为了简单起见,后面不对算法是每个公式的设计思想进行详细解释,而是直接介绍计算公式。NOA的位置更新公式较多,与HHO算法的框架相似,比较复杂。因此这里主要是帮助大家把框架理清楚,清楚怎么算就行。以下是我的解读(公式序号与原文有出入,我改变了序号,方便理解):

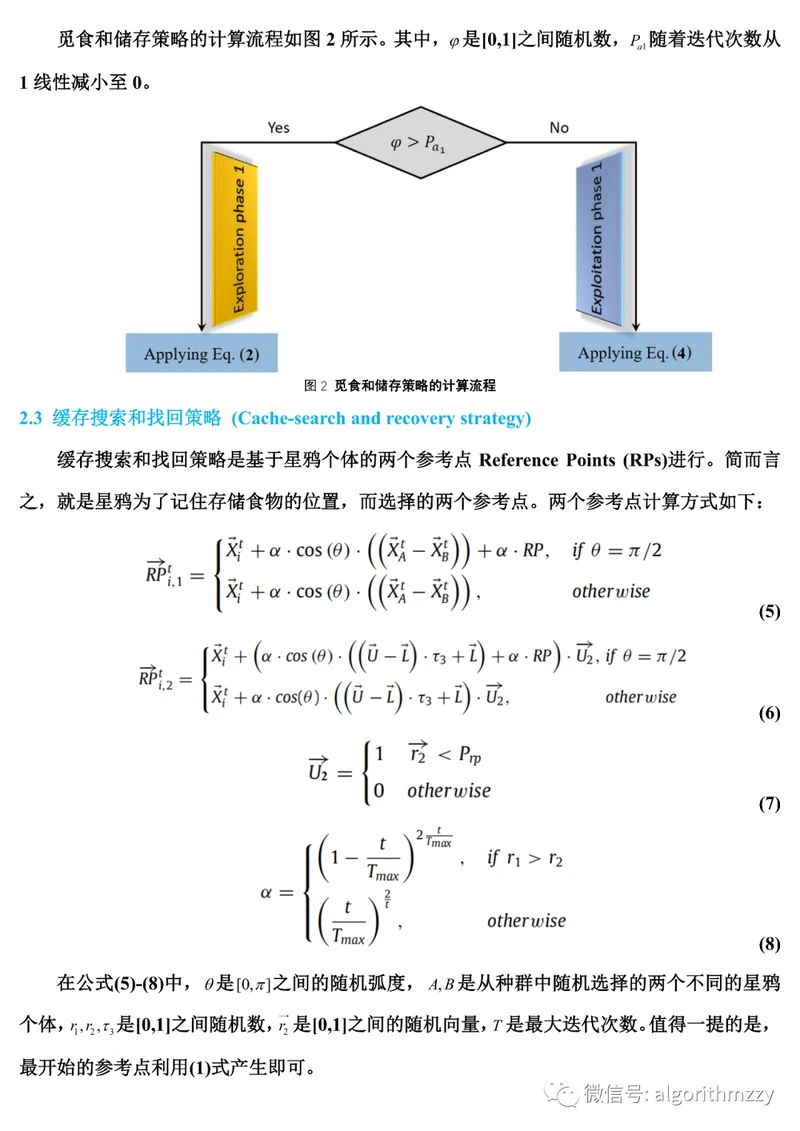

03
计算流程
NOA的计算流程图如图4所示(注意:图4截止NOA的原文,因此公式的对应序号与前面不一样,图4中的公式需要对照原文看):
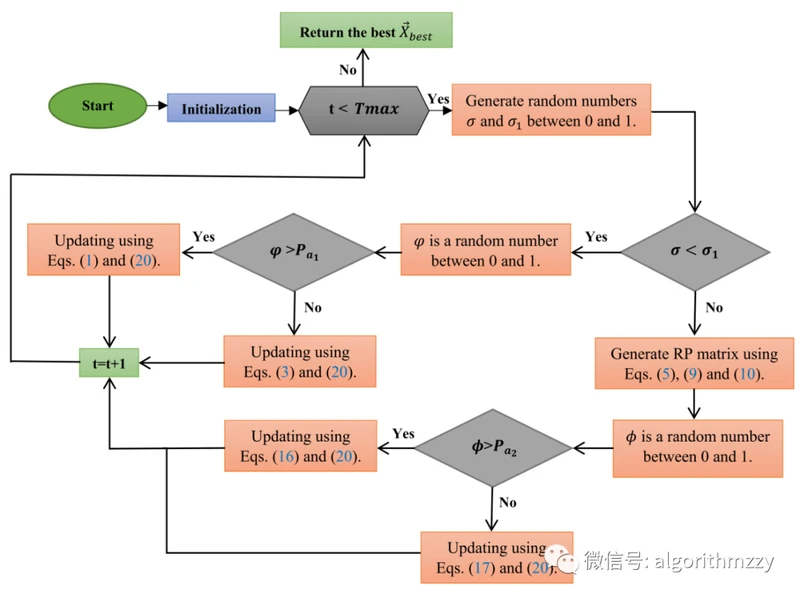
图4 NOA的计算流程
04
实验仿真
NOA的算法性能很优秀,并且,它的计算时间并没有因为公式的数量而变得冗长,计算速度较快。比较推荐这个算法。
这里对NOA的性能进行简单的测试。将NOA用于函数寻优,算法的MATLAB程序是严格按照它的原始参考文献进行编码的。此外,种群规模取的50,Benchmark函数分别采用了CEC2005测试集、CEC2013测试集、CEC2014测试集、CEC2017测试集、CEC2020优化函数测试集和CEC2022优化函数测试集。对比算法选择:灰狼优化(GWO)、鲸鱼优化算法(WOA)、哈里斯鹰优化(HHO)、非洲秃鹫优化算法(AVOA)、蜣螂优化(DBO)和沙猫群优化(SCSO),这六种算法都是今年来提出的优秀算法,认可度较高。这里对仿真结果进行简要展示,就不再进一步做分析了。
首先,我们来检验一下NOA对全局勘探和局部开发的平衡能力。如图5所示,是NOA在CEC2005测试函数f7上的勘探和开发占比曲线。
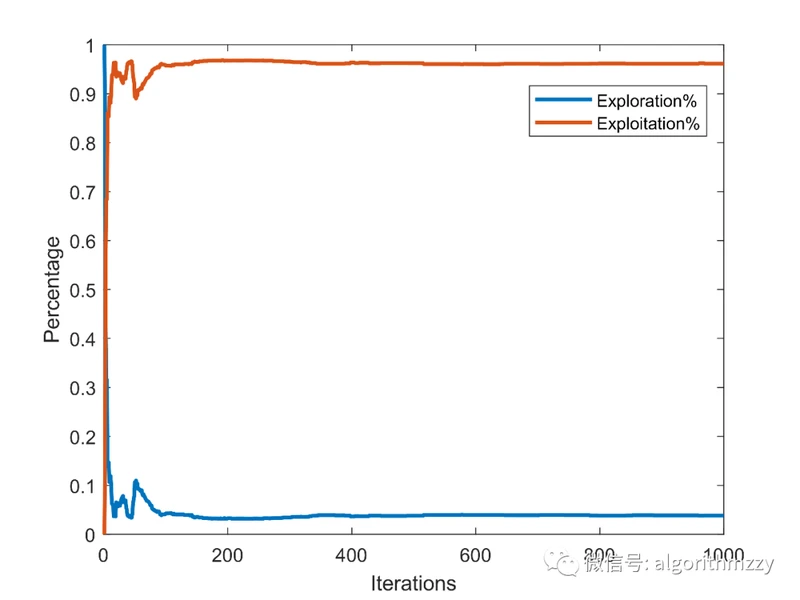
图5 NOA在CEC2005 f7上的勘探和开发百分占比变化曲线
其次,以CEC2005测试集中的单峰函数f1和多峰函数f10为例,展示七种算法在30维环境下的收敛效果,如图6所示。
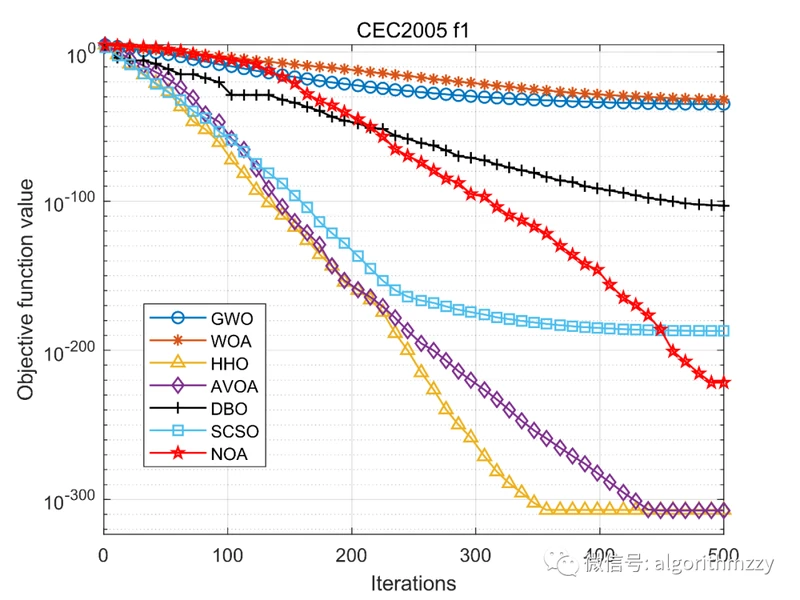
(a) f1
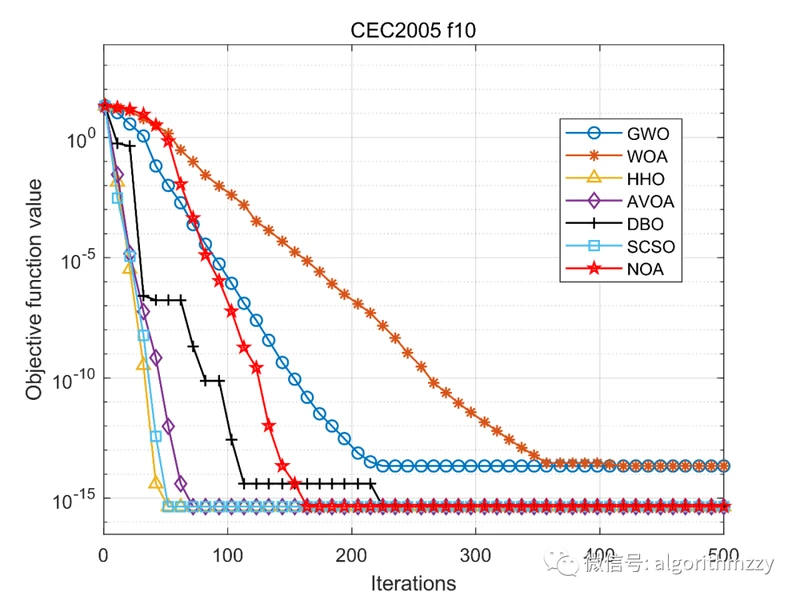
(b) f10
图6 七种进化算法在CEC2005两个测试函数上的收敛曲线
再次,以CEC2013测试集中的单峰函数F1为例,展示七种算法在30维环境下的收敛效果,如图7所示。(注意是画的误差曲线)
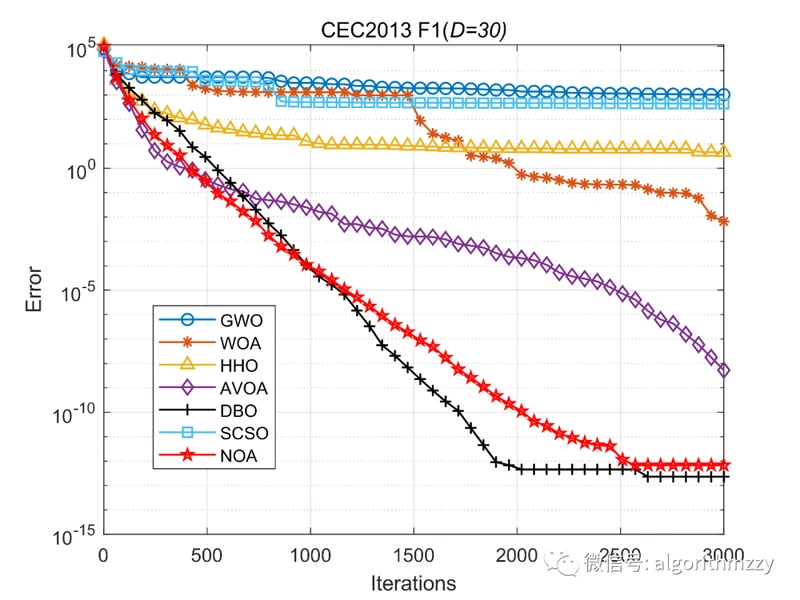
图7 七种进化算法在CEC2013 F1上的误差收敛曲线
接着,以CEC2014测试集中的单峰函数F3为例,展示七种算法在30维环境下的收敛效果,如图8所示。(注意是画的误差曲线)
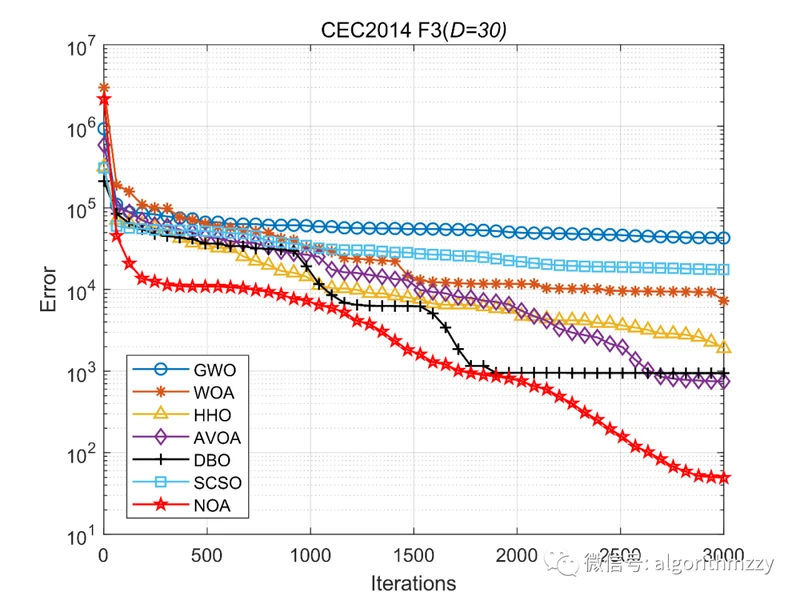
图8 七种进化算法在CEC2014 F3上的误差收敛曲线
再然后,以CEC2017测试集中的混合函数F14为例,展示七种算法在30维环境下的收敛效果,如图9所示。(注意是画的误差曲线)
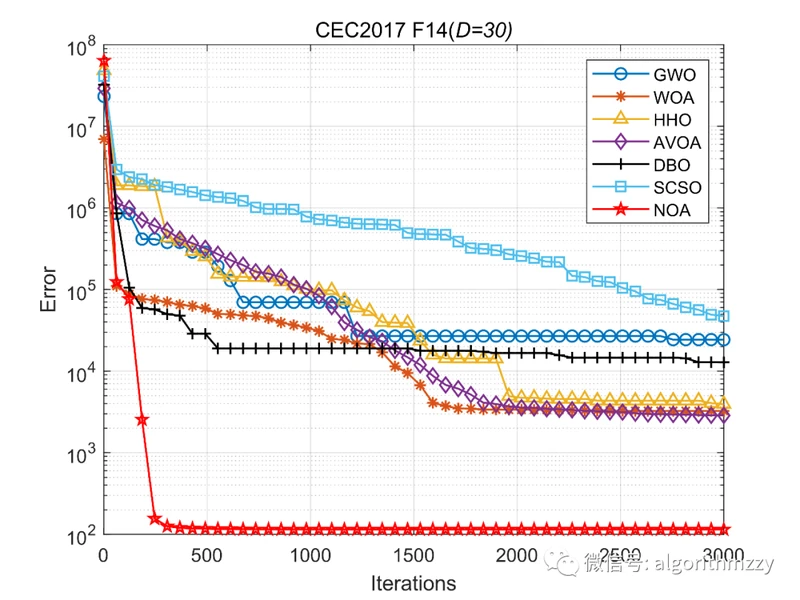
图9 七种进化算法在CEC2017 F14上的误差收敛曲线
紧接着,以CEC2020优化函数测试集中的混合函数F5为例,展示七种算法在10维环境下的收敛效果,如图10所示。(注意是画的误差曲线)
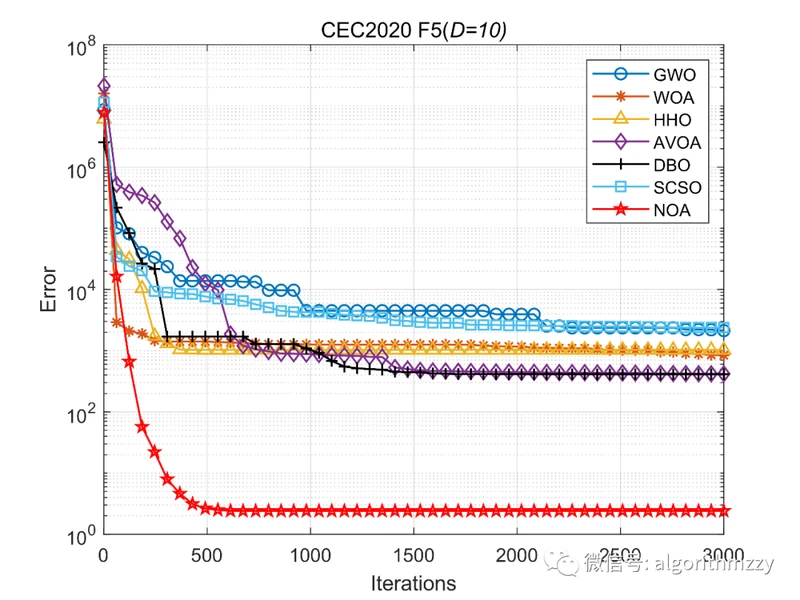
图10 七种进化算法在CEC2020 F5上的误差收敛曲线
最后,以CEC2022优化函数测试集中的基本多模态函数F3为例,展示七种算法在10维环境下的收敛效果,如图11所示。(注意是画的误差曲线)
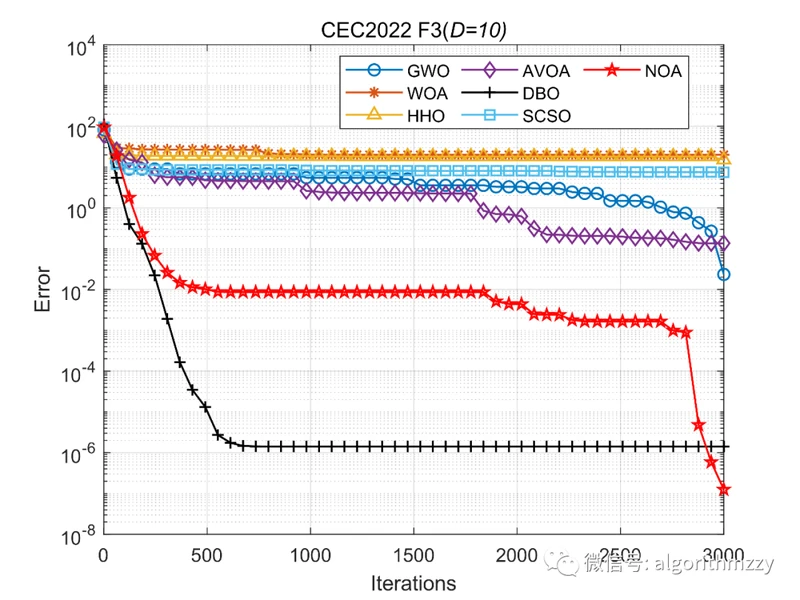
图11 七种进化算法在CEC2022 F3上的误差收敛曲线
不难看出,无论是与HHO、AVOA、SCSO等优秀算法相比,还是和目前火热的DBO算法相比,NOA都能在不同的复杂测试集上展现出明显的优势,算法性能优越,具备较强的竞争力。大家可以进一步了解一下这个算法。
进一步,可将NOA应用于复杂工程约束优化问题,例如之前推送的两期算法应用内容:
算法应用:基于DBO算法的工程优化设计(第1期)(含MATLAB代码)
算法应用:工程优化设计(第2期)(含MATLAB代码)
机器人夹持器问题(Robot gripper problem)通过考虑七个连续的设计变量和几何尺寸,要求在夹持器末端位移范围内夹持器所施加的最大和最小力之差最小。其数学模型如下:

这里以机器人夹持器问题为例,展示求解效果,NOA的收敛曲线如图12所示。
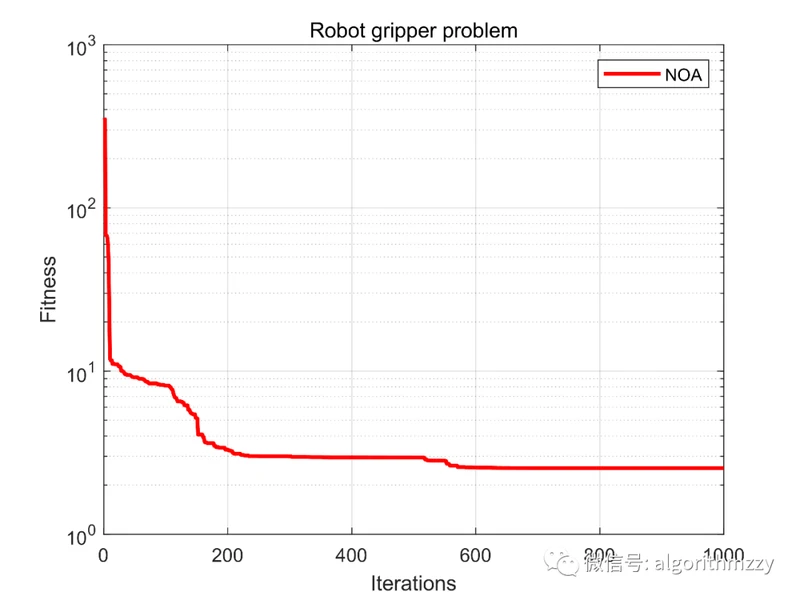
图12 NOA在机器人夹持器问题上的目标函数收敛曲线
05
MATLAB代码
NOA跑CEC2005测试集:
关注公众号:启发式算法讨论
NOA跑CEC2013测试集:
关注公众号:启发式算法讨论
NOA跑CEC2014测试集:
关注公众号:启发式算法讨论
NOA跑CEC2017测试集:
关注公众号:启发式算法讨论
NOA跑CEC2020优化函数测试集:
关注公众号:启发式算法讨论
NOA跑CEC2022优化函数测试集:
关注公众号:启发式算法讨论
NOA的勘探(Exploration)和开发(Exploitation)占比分析:
关注公众号:启发式算法讨论
NOA的工程应用(第1期):压力容器设计、滚动轴承设计、拉伸/压缩弹簧设计、悬臂梁设计、轮系设计、三杆桁架设计。
关注公众号:启发式算法讨论
NOA的工程应用(第2期):焊接梁设计、多盘离合器制动器设计问题、步进圆锥滑轮问题、减速机设计问题、行星轮系设计优化问题、机器人夹持器问题。
关注公众号:启发式算法讨论
