一、余弦距离
1.1 余弦相似度
余弦相似度是用来衡量两个非零向量之间的夹角的余弦值。对于两个向量 A A A 和 B B B,余弦相似度的计算公式为:
C o s i n e S i m i l a r i t y ( A , B ) = A ⋅ B ∥ A ∥ ∥ B ∥ {\rm{Cosine Similarity }}\left( { {\rm{A,B}}} \right) = \frac{ {A \cdot B}}{ {\parallel A\parallel \parallel B\parallel }} CosineSimilarity(A,B)=∥A∥∥B∥A⋅B
1.2 余弦距离(Cosine Distance)
余弦距离是余弦相似度的补数,即:
C o s i n e D i s t a n c e ( A , B ) = 1 − C o s i n e S i m i l a r i t y ( A , B ) {\rm{Cosine Distance }}\left( {
{\rm{A,B}}} \right) = 1 - {\rm{Cosine Similarity }}\left( {
{\rm{A,B}}} \right) CosineDistance(A,B)=1−CosineSimilarity(A,B)
余弦距离的值范围在0到2之间,越接近0表示两个向量越相似,越接近2表示越不相似。
二、马氏距离
马氏距离是一种测量两个点之间距离的方法,不同于欧几里得距离,它考虑了数据的协方差。
定义:设 x x x和 y y y是从均值为 μ \mu μ,协方差矩阵为 Σ \Sigma Σ(>0)的样本总体 π \pi π中抽取的两个样品( p p p维),则:
x x x到 y y y之间的平方马氏距离定义为:
d 2 ( x , y ) = ( x − y ) T Σ − 1 ( x − y ) {d^2}(x,y) = {(x - y)^T}{
{\bf{\Sigma }}^{ - 1}}(x - y) d2(x,y)=(x−y)TΣ−1(x−y)
若协方差是单位矩阵,即:所有变量之间的协方差都为零,那么数据的各个特征(维度)是相互独立的,且每个特征的方差都等于1。在这种情况下,马氏距离可以简化为欧式距离,因为协方差矩阵的逆矩阵就是单位矩阵。
2.1 方差(Variance)
方差是用来度量单一随机变量的分散程度或波动性的统计量。衡量数据点与数据集均值之间的离散程度。方差越大,数据点越分散,对于随机变量 x x x,其方差计算如下:
V a r ( X ) = σ x 2 = 1 n − 1 ∑ i = 1 n ( x i − x ˉ ) 2 {\rm{Var}}(X) = \sigma _x^2 = \frac{1}{
{n - 1}}\sum_{i=1}^n (x_i - \bar{x})^2 Var(X)=σx2=n−11i=1∑n(xi−xˉ)2
在计算样本方差时,我们通常将分母中的除数设为 ( n − 1 ) (n - 1) (n−1) 而不是 n n n。这是因为计算样本方差的目的是估计总体方差,而在估计过程中需要考虑样本的大小对估计精度的影响。这种校正的目的是为了更准确地估计总体方差,因为样本方差通常会略微低估总体方差。
当将除数设为 ( n − 1 ) (n - 1) (n−1) 时,称为自由度调整。自由度调整的原因在于样本中的数据点之间并不是完全独立的,而是相互关联的。如果我们仅将除数设为 n n n,那么样本方差可能会过低估计总体方差,因为它没有考虑到样本中的这种关联性。
自由度调整考虑了这种关联性,通过将除数设为 ( n − 1 ) (n - 1) (n−1) 来更准确地估计总体方差。这意味着我们不会过于乐观地估计总体方差,从而更好地反映了总体的分散性。这对于统计推断和参数估计非常重要,因为我们希望我们的估计尽可能接近总体参数的真实值。
总结一下,自由度调整的目的是减小样本方差的偏差,使其更接近总体方差的真实值,从而提高统计估计的准确性。这是统计学中常见的惯例。
2.2 协方差(Covariance)
协方差用于度量两个随机变量之间的线性关系,即它度量这两个变量如何一起变化。对于两个随机变量 X X X 和 Y Y Y,它们的协方差可以用以下公式计算:
σ ( x , y ) = 1 n − 1 ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) \sigma(x, y) = \frac{1}{
{n - 1}} \sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y}) σ(x,y)=n−11i=1∑n(xi−xˉ)(yi−yˉ)
上述公式是样本协方差的计算方法。若有整个总体的数据,可以将 (n - 1) 改为 n,得到总体协方差。
C o v ( X , Y ) = E [ ( X − μ x ) ( Y − μ y ) ] {\rm{Cov}}(X,Y) = E\left[ {\left( {X - {\mu _x}} \right)\left( {Y - {\mu _y}} \right)} \right] Cov(X,Y)=E[(X−μx)(Y−μy)]
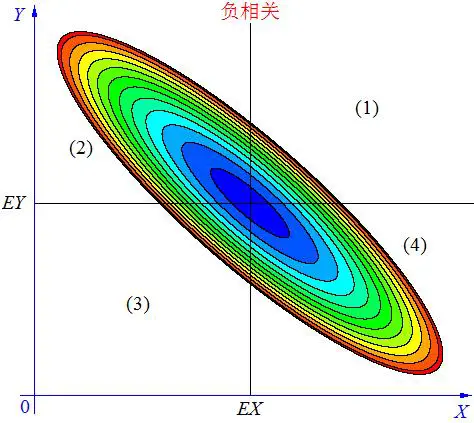
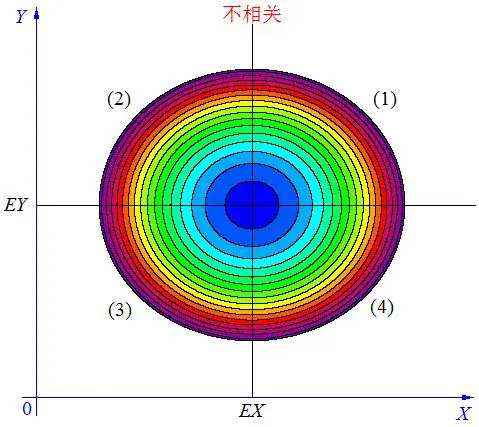
正协方差表示两个变量正相关,负协方差表示两个变量负相关,零协方差表示两个变量不相关。

2.3 皮尔逊相关系数(Pearson Correlation Coefficient)
协方差的值可以为正、负或零,但它本身并没有标准化,因此很难用来比较不同数据之间的关系。为了更容易理解变量之间的关系,通常会将协方差标准化为相关系数(Correlation Coefficient),也称为皮尔逊相关系数。相关系数的范围在 -1 到 1 之间,更容易解释和比较不同数据集的关系,为 -1 表示完全负相关,1表示完全正相关,0 表示没有线性关系。相关系数的计算公式如下:
r = C o v ( X , Y ) σ X σ Y r = \frac{
{
{\rm{Cov}}(X,Y)}}{
{
{\sigma _X}{\sigma _Y}}} r=σXσYCov(X,Y)
其中 σ X {\sigma _X} σX和 σ Y {\sigma _Y} σY分别是 X X X和 Y Y Y标准差。
