现在面临一个问题。
有三个人,A、B、C:

有三个物品,1、2、3:

需要将这三个物体分给三个人,每人一个。每个人对三个物品的喜好不同,要怎样分配才能让三个人的总满意度最高?
分配问题 广泛存在于生产和生活中。例如为一组工作人员分配任务,或者为作战小组分配进攻目标等等。在分配过程中,精明的分配者一定会实现某个目的,例如让每个工作人员充分发挥专长,最高质量地完成任务;或者为每个作战小组分配相距最近的进攻目标,最快速地结束战斗。怎样分配能实现这些目的,就是分配问题的解。
拍卖算法是用来解决这类问题的经典算法,灵感来自于经济活动中的拍卖过程,是一种能够在有限步计算中获得最佳分配的算法。
回到我们开始时的例子。A先生擅长球类运动,滑板也略有涉及,但是对在海浪里穿梭这项运动并不感冒。因此A先生最想要网球拍,有点想要滑板,完全不想要冲浪板。根据三个物品对于A先生的重要性,我们为这三项物品打分为4、2、0。在这个例子中,我们打分并没有复杂的规则:某人想要某件物品的愿望越迫切,打分越高。同样,其余两位也表达了自己的喜好。于是我们得到了下面这张图。
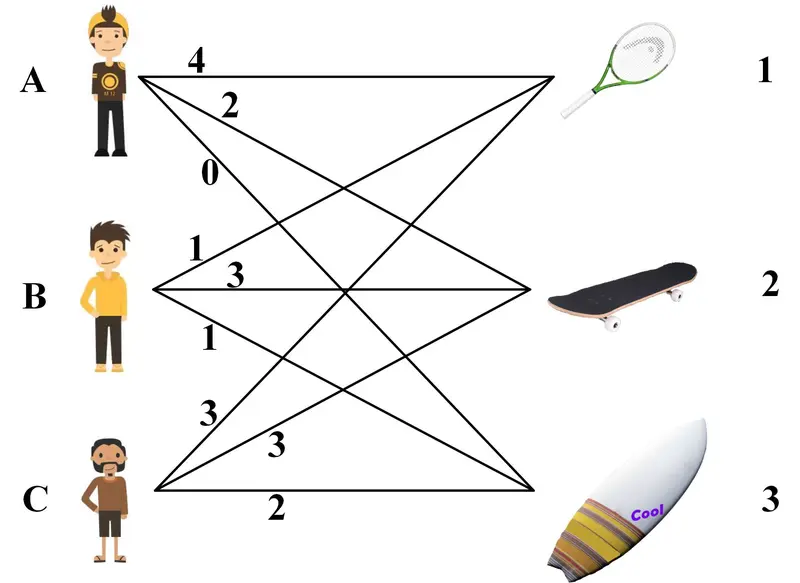
图中线上的数字表示某人对某物品的打分,也就是喜好。从物品的角度而言,线上的数字代表如果某一个物体被分配给了某个人,将会给这个人带来多少好处(即,价值 Value,文献中常用 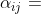 表示 j 物品分配给第 i 个人的价值)。
表示 j 物品分配给第 i 个人的价值)。
为了实现总体满意度最高的分配,三位先生坐在一起竞争物品的归属。按照商业原则,当我们和竞争对手想买同一件物品时,我们必须付比对手更多的钱(即,价格 Price,文献中常用 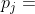 表示 j 物品的价格),才能将物品据为己有。于是三位先生开始对物品报价。
表示 j 物品的价格),才能将物品据为己有。于是三位先生开始对物品报价。
在首次出价之前,三个物品的起拍价都是0。
A先生首先出价。对于A先生而言,目前三个物品的价格都是0。如果A先生选择购买1物品,那么花费0元购得4点的价值,A先生这笔交易的收益(即,净利润 Profit) 为 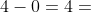 。
。
重要公式1: 收益计算公式 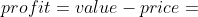
A先生购买1、2、3三个物品的收益分别为4、2、0。算法为每个人赋予了自利性,即总是选择收益最高的物品,这也是算法最终得到最优解的重要保证。基于自利性,A先生选择了1物品,并对1物品报价,提高了它的价格。价格提高的幅度在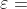 到
到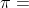 之间,即每次报价最少比原来提高
之间,即每次报价最少比原来提高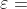 ,最多比原来提高
,最多比原来提高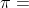 (增幅范围的意义和
(增幅范围的意义和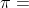 的详细计算将在下文中阐述,本例中选取
的详细计算将在下文中阐述,本例中选取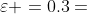 )。
)。
重要公式2:报价计算公式 
A先生将物品1的价格提高到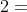 ,局面变成了下图。
,局面变成了下图。

B先生开始报价。他购买1、2、3三个物品的收益分别是 -1.3、3、1。由于A先生的提价,1物品的价格已经高于1物品能够提供给B先生的价值,因此B先生不会再考虑1物品。B先生选择了收益最高的2物品,并提升了它的价格至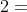 ,如下图所示。
,如下图所示。
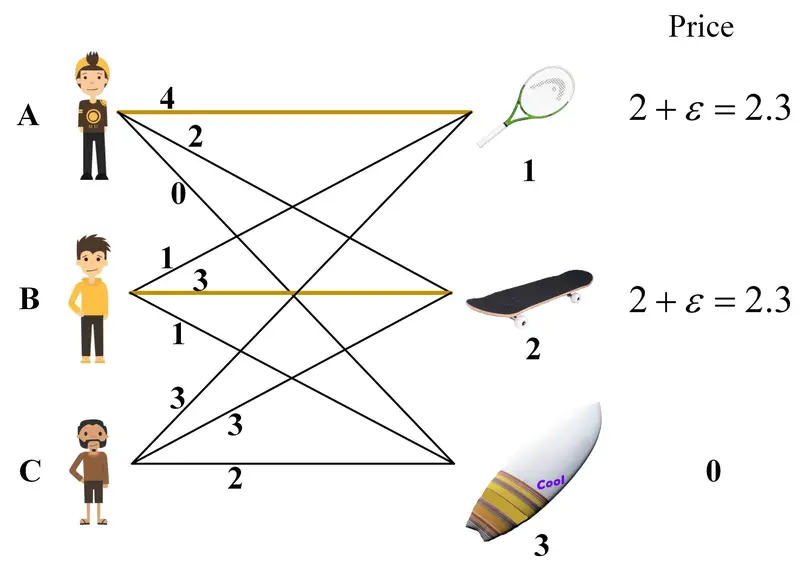
C先生开始报价。他购买1、2、3三个物品的收益分别是 0.7、0.7、2。根据自利性,C先生选择3物品,并修改3物品的价格为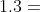 ,如下图所示。
,如下图所示。
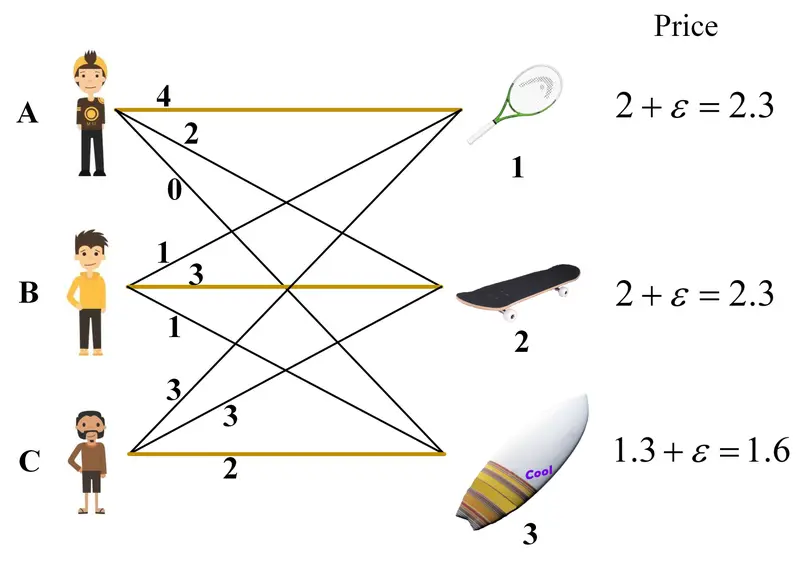
到此步为止,所有人都得到了分配,算法终止。分配结果中,总体满意度(喜好值的和)为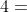 ,是在所有分配方案中总体满意度最高的方案。
,是在所有分配方案中总体满意度最高的方案。
算法停止条件:当每个人都获得分配 或者 每个人购买所有物品的最大收益都不大于0。
还有一个疑问,我们应该如何控制报价的增长?
如果我们不限制报价增长幅度的下限,那么当两个人对同一物品展开竞价时,价格提升的会很慢,甚至完全没有提升,竞价将会永无止境的持续下去;
如果我们不限制报价增长幅度的上限,那么一次报价就可能使物品的价格超过价值,导致无法参与后续的拍卖。
因此我们限制报价增幅的上下限。
重要推论1:对于n人n物品的分配,当价值 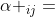 (即图中横线上标注的数字)为整数时,若
(即图中横线上标注的数字)为整数时,若
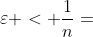
则算法结束时获得最优解。
在上例中,有3个人参与分配, ,因此我们选取
,因此我们选取 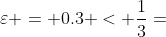
重要公式3:如果除了当前要提价的 j 物品之外,没有其它能够提供正收益的物品,则

如果除了当前要提价的 j 物品之外,还有一个物品 k ,购买它产生的收益仅次于物品 j,则
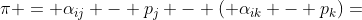
例如在第一步A先生提价的过程中,最高收益来自于1物品,收益为4。物品2也提供大于零的收益,为2,仅次于1物品提供的收益。由公式3可以得到
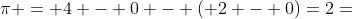
由于提价过程中给出的是一个范围,在设计算法时,一般采用上限值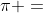 作为提价的幅度,因为提价的幅度越高,算法结束的越快。在许可的范围内取最大幅度,即可保证最优性,又可以加快算法速度。
作为提价的幅度,因为提价的幅度越高,算法结束的越快。在许可的范围内取最大幅度,即可保证最优性,又可以加快算法速度。
扩展阅读:
拍卖算法的开山之作:
Dimitri P. Bertsekas, A Distributed Algorithm for the Assignment Problem, 1979
论文链接:http://web.mit.edu/dimitrib/www/Orig_Auction.pdf
